آموزش پیش‌بینی سری زمانی

داده‌های سری زمانی داده‌هایی هستند که از یک موضوع مشخص در نقاط مختلف زمان جمع‌آوری می‌شوند؛ مانند تولید ناخالص داخلی (GDP) یک کشور در هر سال، قیمت سهام یک شرکت در طول یک دوره زمانی، یا ضربان قلب شما که در هر ثانیه ثبت شده است.

هر داده‌ای که بتوان آن را به طور پیوسته در بازه‌های زمانی مختلف ثبت کرد، شکلی از داده‌های سری زمانی است. در ادامه یک نمونه از داده‌های سری زمانی را مشاهده می‌کنید که تعداد موارد ابتلا به کووید-19 در ایالات متحده را بر اساس گزارش‌های ارسالی به CDC نشان می‌دهد. محور افقی گذر زمان و محور عمودی تعداد موارد ابتلا را بر حسب هزار نفر نمایش می‌دهد.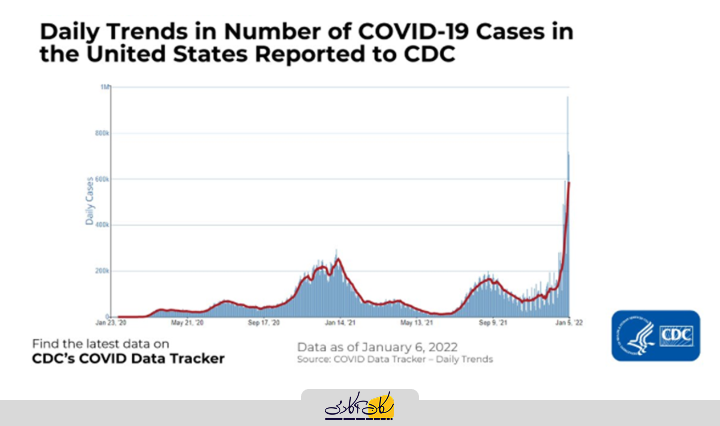

از سوی دیگر، مجموعه‌ داده‌هایی که اطلاعات را در یک لحظه مشخص از زمان ثبت می‌کنند (برای مثال اطلاعات مشتریان) به عنوان داده‌های مقطعی (Cross-sectional) شناخته می‌شوند. به ‌عنوان نمونه، در مجموعه‌داده‌ای که در ادامه آمده است، کشورهایی با بیشترین موارد ابتلای کووید-19 در یک بازه زمانی ثابت و یکسان برای همه کشورها بررسی شده‌اند.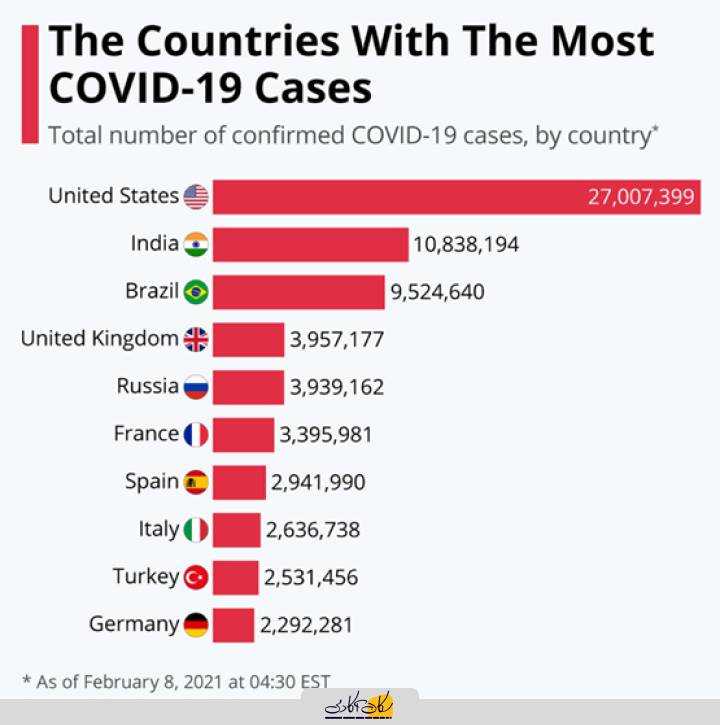

تشخیص تفاوت میان داده‌های مقطعی و داده‌های سری زمانی دشوار نیست، زیرا اهداف تحلیل هر دو نوع داده کاملاً با هم متفاوت است. در مثال‌های بالا، ابتدا به بررسی تعداد موارد ابتلا به کووید-19 در طی یک دوره زمانی پرداختیم (سری زمانی)، سپس موارد ابتلا را بین کشورها در یک بازه زمانی معین مقایسه کردیم (داده مقطعی).

یک مجموعه داده واقعی معمولاً ترکیبی از این دو قالب است. برای مثال، فروشگاه زنجیره‌ای x را در نظر بگیرید که روزانه هزاران محصول می‌فروشد. اگر فروش محصولات را در یک روز مشخص مورد بررسی قرار دهید، این یک تحلیل مقطعی خواهد بود؛ مثلاً شاید بخواهید بدانید در شب کریسمس پرفروش‌ترین کالا چیست. در مقابل مثالی که برای تحلیل سری زمانی است، فروش یک محصول خاص در طول یک دوره زمانی (مثلاً 5 سال گذشته) ، یک تحلیل سری زمانی است.

اهداف در هنگام تحلیل داده‌های سری زمانی و داده‌های مقطعی متفاوت است و یک مجموعه‌داده واقعی اغلب ترکیبی از هر دو نوع داده خواهد بود.

پیش‌بینی سری زمانی چیست؟

پیش‌بینی سری زمانی (Time Series Forecasting) دقیقاً همان چیزی است که از نام آن به ذهن می‌رسد: پیش‌بینی مقادیر ناشناخته در آینده. پیش‌بینی سری زمانی شامل جمع‌آوری داده‌های تاریخی، آماده‌سازی آن‌ها برای الگوریتم‌ها و سپس پیش‌بینی مقادیر آینده بر اساس الگوهایی است که از داده‌های تاریخی آموخته شده‌اند.

شرکت‌ها ممکن است به دلایل متعددی به پیش‌بینی مقادیر آینده علاقه‌مند باشند، مانند فروش ماهانه، موجودی انبار، نرخ بیکاری و دمای جهانی. برای مثال:

1. یک خرده‌فروش ممکن است علاقه‌مند باشد تا فروش آینده را در سطح SKU (کد شناسایی محصول) پیش‌بینی کند تا برای برنامه‌ریزی و بودجه‌بندی تصمیم‌گیری کند.
2. یک فروشنده کوچک ممکن است بخواهد فروش را بر حسب فروشگاه پیش‌بینی کند تا بتواند منابع انسانی را متناسب با فصول پرفروش یا کم‌فروش تنظیم کند.
3. یک غول نرم‌افزاری مانند گوگل ممکن است بخواهد پرترافیک‌ترین ساعت روز یا شلوغ‌ترین روز هفته را پیش‌بینی کند تا منابع سرور را مطابق آن برنامه‌ریزی نماید.
4. یک نهاد بهداشتی ممکن است به پیش‌بینی مجموع واکسیناسیون‌های کووید انجام‌شده علاقه‌مند باشد تا بتواند زمان تقریبی رسیدن به ایمنی جمعی را برآورد کند.

 انواع پیش‌بینی سری زمانی

سه نوع اصلی پیش‌بینی سری زمانی وجود دارد و انتخاب نوع مناسب بستگی به نوع داده‌ای که با آن سروکار دارید و کاربرد مورد نظرتان دارد.

1. پیش‌بینی تک‌متغیره (Univariate Forecast)

سری زمانی تک‌متغیره، همان‌طور که از نامش پیداست، سری زمانی‌ای است که تنها یک متغیر وابسته به زمان دارد. برای مثال، اگر در حال ردیابی مقادیر دما در هر ساعت برای یک منطقه مشخص باشید و بخواهید دمای آینده را صرفاً با استفاده از دماهای تاریخی پیش‌بینی کنید، این یک مثال از پیش‌بینی سری زمانی تک‌متغیره است. داده شما در این حالت، ممکن است به صورت  زیر باشد: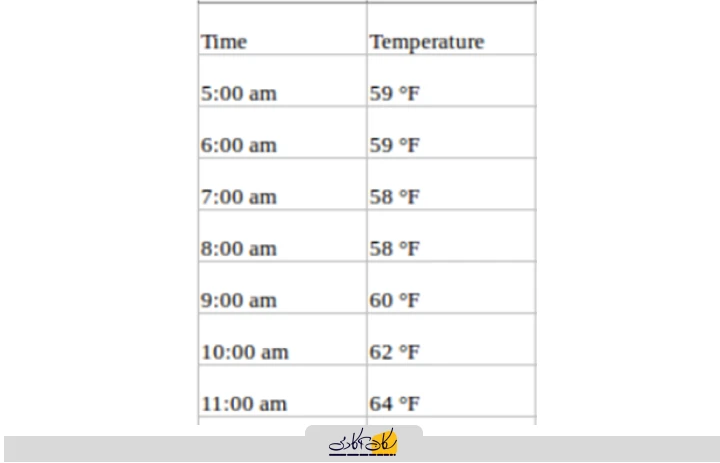

2.پیش‌بینی چندمتغیره (Multivariate Forecast)

از سوی دیگر، سری زمانی چندمتغیره بیش از یک متغیر وابسته به زمان دارد. هر متغیر نه‌تنها به مقادیر گذشته خود وابسته است، بلکه ممکن است تحت تأثیر سایر متغیرها نیز قرار گیرد و از همه این وابستگی‌ها برای پیش‌بینی مقادیر آینده استفاده می‌شود.

به مثال قبل بازگردیم و فرض کنیم مجموعه ‌داده ما شامل ویژگی‌های مرتبط با هواشناسی در همان بازه زمانی نیز باشد؛ مثلاً درصد رطوبت، نقطه شبنم  (Dew Point)، سرعت باد و ...، در کنار مقادیر دما (چنین مجموعه ‌داده ای ممکن است به شکل زیر باشد). در این شرایط، برای پیش‌بینی دما، باید چندین متغیر را در نظر بگیریم. بنابراین این نوع داده‌ها در دسته سری‌های زمانی چندمتغیره قرار می‌گیرند.

در اینجا، هنگام پیش‌بینی مقادیر آینده دما، لازم است از سایر اطلاعات موجود نیز استفاده کنید، زیرا فرض بر این است که مقادیر دما تحت تأثیر این عوامل نیز قرار می‌گیرند.

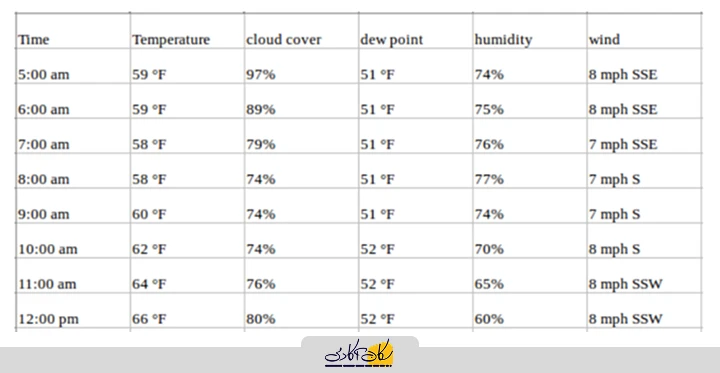
هنگامی که با پیش‌بینی سری زمانی چندمتغیره سروکار داریم، متغیرهای ورودی می‌توانند دو نوع باشند:

• برون‌زا (Exogenous): متغیرهای ورودی که تحت تأثیر سایر متغیرهای ورودی قرار نمی‌گیرند، اما متغیر خروجی به آن‌ها وابسته است.
• درون‌زا (Endogenous): متغیرهای ورودی که تحت تأثیر سایر متغیرهای ورودی قرار دارند و متغیر خروجی نیز به آن‌ها وابسته است.

برای درک بهتر این موضوع، باید بدانیم که برخی از مدل‌های کلاسیک سری زمانی تنها برای پیش‌بینی‌های تک‌متغیره طراحی شده‌اند و از پیش‌بینی سری‌های زمانی چندمتغیره پشتیبانی نمی‌کنند. در چنین مواردی، مدل‌های یادگیری ماشین وارد عمل می‌شوند.

یکی از مزایای اصلی این مدل‌های کلاسیک، انعطاف‌پذیری بالای آن‌هاست که به شما اجازه می‌دهد تقریباً هر مسئله پیش‌بینی سری زمانی را به‌عنوان یک مسئله رگرسیون مدل‌سازی کنید. به این فرآیند، رگرسیون سری زمانی (Sequence Regression) گفته می‌شود، که در آن مقادیر گذشته و متغیرهای مستقل دیگر به عنوان ورودی مدل در نظر گرفته می‌شوند تا مقادیر آینده را پیش‌بینی کنیم (برای اطلاعات بیشتر می‌توانید به دوره آموزش رگرسیون سکان آکادمی مراجعه کنید).

در این آموزش، چندین مدل کلاسیک و محدودیت‌های آن‌ها را بررسی خواهیم کرد و سپس به معرفی مدل‌های یادگیری ماشین خواهیم پرداخت. 

روش‌های پیش‌بینی سری زمانی

پیش‌بینی سری زمانی را می‌توان به طور کلی به دسته‌های زیر تقسیم کرد:

1. مدل‌های کلاسیک/آماری:

• میانگین‌های متحرک (Moving Averages)
• هموارسازی نمایی (Exponential Smoothing)
• ARIMA
• SARIMA
• TBATS

2.یادگیری ماشین:

• رگرسیون خطی، (XGBoost)
• جنگل تصادفی (Random Forest)
• یا هر مدل یادگیری ماشینی همراه با روش‌های کاهشی

3.یادگیری عمیق:

• RNN
• LSTM

ما در این آموزش فقط به مدل‌ کلاسیک/آماری و یادگیری ماشین می‌پردازیم.

👈 برای آشنایی با مدل یادگیری عمیق و RNN به دیگر مطالب موجود در سایت سکان آکادمی مانند مقاله‌ی شبکه عصبی عمیق بازگشتی (RNN) مراجعه کنید.

مدل‌های آماری

وقتی صحبت از پیش‌بینی سری زمانی با استفاده از مدل‌های آماری به میان می‌آید، الگوریتم‌های محبوب و پذیرفته‌شده متعددی وجود دارند. هر کدام از این مدل‌ها مبانی ریاضی خاص خود و مفروضات ویژه‌ای دارند که باید رعایت شوند. در این آموزش، وارد جزئیات عمیق ریاضی نمی‌شویم و تنها تصویری کلی ارائه می‌دهیم که امیدواریم برای شما مفید باشد.

1. ARIMA

مدل ARIMA یکی از محبوب‌ترین روش‌های کلاسیک برای پیش‌بینی سری‌های زمانی است. نام این مدل مخفف عبارت Autoregressive Integrated Moving Average  است. ARIMA پیش‌بینی‌های خود را بر اساس مقادیر گذشته سری زمانی انجام می‌دهد و از وقفه‌های (lags) گذشته سیگنال و خطاهای پیش‌بینی قبلی استفاده می‌کند. این مدل سه مؤلفه اصلی دارد:

• Autoregression (AR) : این مولفه به فرایند تفاضل‌گیری (Differencing) از داده‌ها اشاره دارد که برای ایستا کردن سری زمانی استفاده می‌شود. در این روش، داده‌ها با اختلاف مقادیر نسبت به مقدار قبلی جایگزین می‌شوند تا روندها و نوسانات پایدارتر شوند.
• (I) Integrated : این بخش به خودهمبستگی اشاره دارد و متغیر را بر اساس مقادیر گذشته خودش مدل‌سازی می‌کند.
• Moving Average (MA): این بخش وابستگی بین مشاهدات و خطاهای پیش‌بینی‌های گذشته را در نظر می‌گیرد و با استفاده از میانگین متحرک روی خطاهای وقفه‌دار، مدل را بهبود می‌بخشد.

به زبان ساده:

• بخش AR نشان می‌دهد که متغیر به کمک مقادیر گذشته خودش مدل‌سازی می‌شود.
• بخش MA  بیانگر این است که خطای پیش‌بینی به صورت ترکیبی خطی از خطاهای قبلی محاسبه می‌شود.
• بخش I بیان می‌کند که داده‌ها با تفاضل‌گیری از مقادیر قبلی به داده‌های ایستا تبدیل شده‌اند (این فرایند ممکن است چندین بار انجام شود).
• هدف اصلی این سه مؤلفه این است که مدل به بهترین شکل ممکن با داده‌ها تطابق پیدا کند و پیش‌بینی‌های دقیقی ارائه دهد.

2. SARIMA

مشکل ARIMA در این است که داده‌های فصلی را مستقیماً پشتیبانی نمی‌کند، اما SARIMA که توسعه‌ای از ARIMA است، مدل‌سازی مستقیم مؤلفه فصلی سری را پشتیبانی می‌کند. داده فصلی یعنی سری زمانی که دارای الگوی تکرار شونده در بازه‌های زمانی مشخص است.

ARIMA انتظار دارد داده غیرفصلی باشد یا مؤلفه فصلی قبلاً حذف شده باشد (مثلاً از طریق تفاضل‌گیری فصلی). در مقابل، SARIMA سه ابرپارامتر جدید به مدل اضافه می‌کند تا خودهمبستگی، تفاضل‌گیری و میانگین متحرک مؤلفه فصلی سری را هم بتواند در نظر بگیرد.

مدل ARIMA با وجود محبوبیتش، به‌طور مستقیم از داده‌های فصلی پشتیبانی نمی‌کند. این یک محدودیت مهم است، زیرا بسیاری از سری‌های زمانی دارای الگوهای تکرارشونده در بازه‌های زمانی مشخص هستند که به آن‌ها داده‌های فصلی گفته می‌شود. برای مثال، فروش یک فروشگاه ممکن است در تعطیلات سالانه افزایش یابد. برای رفع این مشکل، مدل SARIMA که نسخه توسعه‌یافته‌ای از ARIMA است، طراحی شده است.

SARIMA مستقیماً مؤلفه فصلی سری زمانی را مدل‌سازی می‌کند. در حالی که ARIMA انتظار دارد داده‌ها غیرفصلی باشند یا مؤلفه فصلی آن‌ها از پیش حذف شده باشد (مثلاً با استفاده از تفاضل‌گیری فصلی)، SARIMA  سه ابرپارامتر اضافی را به مدل اضافه می‌کند. این ابرپارامترها امکان در نظر گرفتن خودهمبستگی، تفاضل‌گیری و میانگین متحرک مؤلفه فصلی را فراهم می‌کنند.

به زبان ساده، SARIMA به ما این امکان را می‌دهد که علاوه بر الگوهای کلی داده، رفتارهای تکرارشونده فصلی را نیز به‌طور مستقیم در مدل پیش‌بینی وارد کنیم، که این موضوع به دقت بیشتر در پیش‌بینی‌های سری زمانی فصلی منجر می‌شود.

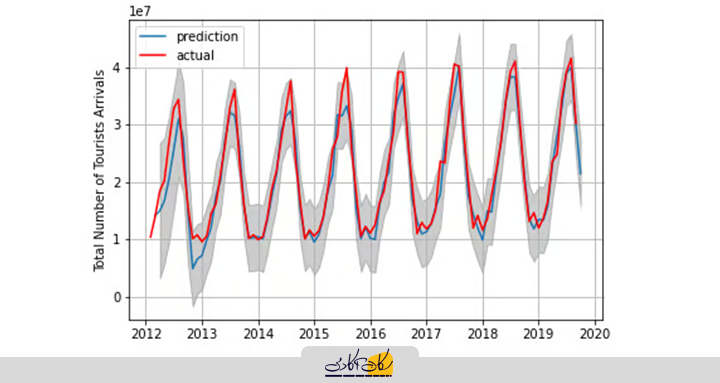
3. هموارسازی نمایی (Exponential Smoothing)

هموارسازی نمایی روشی برای پیش‌بینی سری زمانی تک‌متغیره است که می‌توان آن را برای داده‌هایی با روند یا مؤلفه فصلی تعمیم داد. این روش جایگزینی برای خانواده مدل‌های ARIMA نیز محسوب می‌شود. در هموارسازی نمایی، وزن‌هایی با کاهش نمایی به مشاهدات جدیدتر تا قدیمی‌تر اختصاص داده می‌شوند. داده‌های قدیمی‌تر وزن کمتری دارند و داده‌های جدیدتر وزن بیشتری می‌گیرند. این روش، به شکل‌های زیر قابل استفاده است:

• هموارسازی نمایی ساده (Single) از یک میانگین متحرک وزنی استفاده می‌کند که وزن‌ها به صورت نمایی کاهش پیدا می‌کنند.
• هموارسازی نمایی هولت (Holt) برای داده‌هایی که دارای روند هستند، عموما نتایج قابل اعتمادتر و دقیق‌تری ارائه می‌دهد.
• هموارسازی نمایی سه‌گانه (Triple) که به عنوان هولت وینترز ضربی (Multiplicative Holt-Winters) نیز شناخته می‌شود، برای سری‌های زمانی با روندهای سهمی‌ شکل یا داده‌هایی که هم روند و هم الگوی فصلی دارند، مناسب‌تر است.

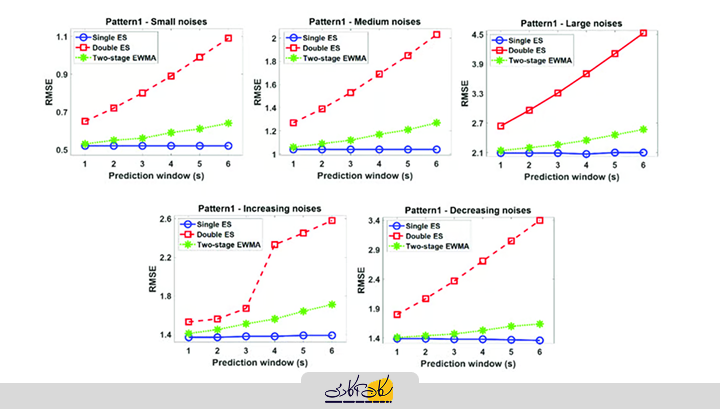
برای مقایسه نتایج بین هموارسازی نمایی ساده (ES)، هموارسازی نمایی دوگانه (Double ES) و میانگین متحرک وزنی نمایی دو مرحله‌ای (Two-step EWMA)، می‌توان موارد زیر را در نظر گرفت:

1. هموارسازی نمایی ساده (ES):

• مناسب برای سری‌های زمانی بدون روند یا الگوهای فصلی.
• تمرکز بر پیش‌بینی مقدار آینده با وزن‌دهی بیشتر به داده‌های اخیر.
• دقت کمتری در داده‌هایی با روند یا فصل‌بندی دارد.

2. هموارسازی نمایی دوگانه (Double ES):

• بهبود یافته برای سری‌های زمانی دارای روند.
• شامل دو مؤلفه است: یکی برای پیش‌بینی مقدار پایه و دیگری برای مدل‌سازی روند.
• عملکرد بهتری نسبت به ES ساده در سری‌های دارای روند دارد.

3. میانگین متحرک وزنی نمایی دو مرحله‌ای (Two-step EWMA):

• ترکیبی از هموارسازی و کاهش نوسانات در داده‌ها.
• مناسب برای داده‌هایی با نویز بالا یا تغییرات شدید.
• انعطاف‌پذیرتر از ES ساده و دوگانه در شرایط خاص.

نتیجه‌گیری کلی:

• ES ساده زمانی کاربرد دارد که داده‌ها فاقد روند یا فصل‌بندی باشند.
• Double ES زمانی مناسب است که سری زمانی دارای روند مشخصی باشد.
• Two-step EWMA در شرایطی که داده‌ها نویز بیشتری دارند یا نیاز به کاهش نوسانات برای شناسایی الگوهای دقیق‌تر است، عملکرد بهتری ارائه می‌دهد.

برای انتخاب روش مناسب، نوع سری زمانی (ثابت، رونددار، یا فصلی) و هدف پیش‌بینی باید مشخص شود.

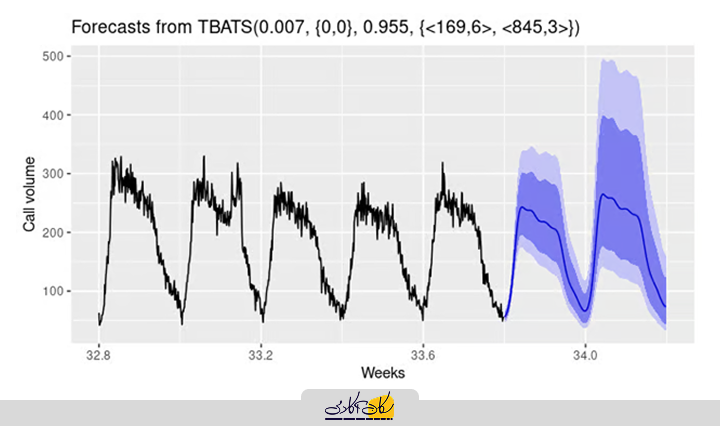
۴. TBATS

مدل‌های TBATS برای داده‌های سری زمانی با چندین فصل (Multiple Seasonality) طراحی شده‌اند. برای مثال، داده‌های فروش خرده‌فروشی ممکن است علاوه بر الگوی روزانه و هفتگی، الگوی سالانه هم داشته‌باشند. در TBATS، ابتدا تبدیل باکس-کاکس (Box-Cox) روی سری زمانی اصلی اعمال می‌شود و سپس این سری به صورت ترکیبی خطی از یک روند هموارشده نمایی، مؤلفه فصلی و مؤلفه ARMA مدل‌سازی می‌گردد.

یادگیری ماشین

اگر نمی‌خواهید از مدل‌های آماری استفاده کنید یا عملکرد آن‌ها رضایت‌بخش نیست، می‌توانید به سراغ روش‌های یادگیری ماشین بروید. یادگیری ماشین رویکردی جایگزین برای مدل‌سازی داده‌های سری زمانی جهت پیش‌بینی است.

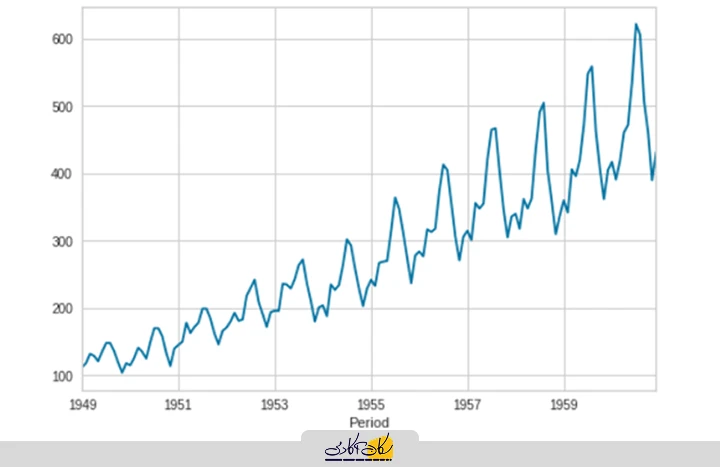
در یادگیری ماشین، ویژگی‌هایی را از تاریخ استخراج کرده و به‌عنوان متغیرهای ورودی (X) استفاده می‌کنیم و مقدار سری زمانی را به‌عنوان متغیر خروجی (y) در نظر می‌گیریم. بیایید مثالی را بررسی کنیم (در این مثال، از مجموعه داده مسافران خطوط هوایی آمریکا استفاده کرده‌ایم که از وبسایت Kaggle قابل دریافت است):

می‌توانیم از ستون "Date" ویژگی‌هایی مانند ماه، سال، هفته سال و ... را استخراج کنیم. برای مثال، نمونه کد زیر را ببینید:

# استخراج ماه و سال از تاریخ
data['Month'] = [i.month for i in data['Date']]
data['Year'] = [i.year for i in data['Date']]

# ایجاد یک دنباله اعداد
data['Series'] = np.arange(1, len(data) + 1)

# حذف ستون‌های غیرضروری و بازچینش
data.drop(['Date', 'MA12'], axis=1, inplace=True)
data = data[['Series', 'Year', 'Month', 'Passengers']]

# نمایش چند ردیف اولیه
data.head()

نمونه ردیف پس از استخراج داده‌ها

نکته مهمی که در این جا باید به آن دقت کنید این است که در تقسیم داده‌ها به مجموعه‌های آموزشی و آزمایشی برای داده‌های سری زمانی باید ترتیب را در نظر بگیرید. شما نمی‌توانید ترتیب زمانی داده‌ها را تغییر دهید یا نمونه‌گیری تصادفی انجام دهید، چون داده آزمایشی باید نقاطی در آینده (نسبت به داده‌های آموزشی) را شامل شود. (زمان همیشه رو به جلو حرکت می‌کند).

# تقسیم داده به آموزش و آزمون
train = data[data['Year'] < 1960]
test = data[data['Year'] >= 1960]

# بررسی ابعاد
train.shape, test.shape
>>> ((132, 4), (12, 4))

اکنون که داده‌ها به دو بخش آموزشی و آزمایشی تقسیم شده‌اند، آماده‌ایم تا یک مدل یادگیری ماشین را روی داده‌های آموزشی، آموزش دهیم، سپس آن را روی داده‌های آزمایشی ارزیابی کرده و عملکرد مدل را بسنجیم. در این مثال، ما از PyCaret استفاده می‌کنیم؛ یک کتابخانه متن‌باز که با آن خیلی کم به کد نویسی نیاز پیدا می کنید و در پایتون گردش کار یادگیری ماشین را به صورت اتوماتیک امکان‌پذیر می‌سازد. برای استفاده از PyCaret ابتدا باید آن را نصب کنید:

pip install pycaret

در صورت نیاز، برای راهنمایی نصب به مستندات رسمی  PyCaret مراجعه کنید. با فرض اینکه PyCaret با موفقیت نصب شده است:

# وارد کردن ماژول رگرسیون PyCaret
from pycaret.regression import *

# مقداردهی اولیه تنظیمات
s = setup(
data = train,
          test_data = test,
          target = 'Passengers',
          fold_strategy = 'timeseries',
          numeric_features = ['Year', 'Series'],
          fold = 3,
          transform_target = True,
          session_id = 123)

اکنون برای آموزش مدل‌های یادگیری ماشین تنها کافیست یک خط دستور را اجرا کنیم:

best = compare_models(sort='MAE')

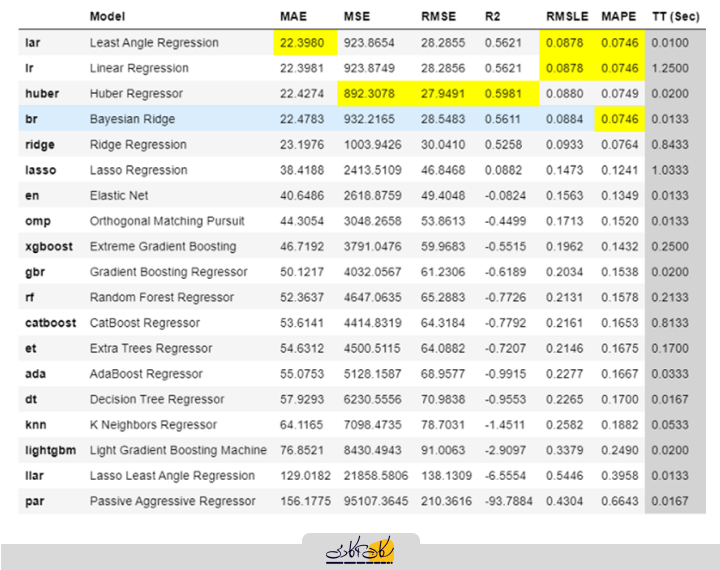
با توجه به نتایج، بهترین مدل بر اساس اعتبارسنجی متقابل سه‌بخشی (3-Fold CV) و معیار خطای مطلق میانگین (MAE)، مدل Least Angle Regression (LAR) است. اکنون می‌توانیم از این مدل برای پیش‌بینی مقادیر آینده استفاده کنیم. برای انجام این کار، مراحل زیر باید انجام شود:

1. ایجاد تاریخ‌های آینده: ابتدا بازه‌های زمانی مورد نظر برای پیش‌بینی (تاریخ‌های آتی) مشخص می‌شود. این بازه‌ها معمولاً به‌صورت گام‌های زمانی مشخص (روزانه، هفتگی یا ماهانه) تعریف می‌شوند.
2. استخراج ویژگی‌ها از تاریخ‌های آتی: پس از تعریف تاریخ‌ها، ویژگی‌های مرتبط (مانند روز هفته، ماه، فصل، یا سایر متغیرهای زمانی) از این تاریخ‌ها استخراج می‌شوند. این ویژگی‌ها به‌عنوان ورودی مدل (X) برای پیش‌بینی استفاده می‌شوند
3. استفاده از مدل برای پیش‌بینی: با استفاده از مدل آموزش‌دیده LAR، مقادیر آینده بر اساس متغیرهای ورودی جدید پیش‌بینی می‌شوند.

این فرآیند تضمین می‌کند که پیش‌بینی‌ها نه تنها بر اساس داده‌های گذشته انجام می‌شوند، بلکه با ویژگی‌های زمانی مرتبط با تاریخ‌های آتی نیز تطبیق دارند. از آنجایی که مدل ما تا سال 1960 آموزش دیده است، بیایید 5 سال آینده تا سال 1965 را پیش‌بینی کنیم. برای استفاده از مدل نهایی برای پیش‌بینی‌های آینده، ابتدا باید مجموعه داده‌ای شامل ستون‌های "Month"، "Year" و "Series" برای تاریخ‌های آینده ایجاد کنیم:

future_dates = pd.date_range(start='1961-01-01', end='1965-01-01', freq='MS')
future_df = pd.DataFrame()
future_df['Month'] = [i.month for i in future_dates]
future_df['Year'] = [i.year for i in future_dates]
future_df['Series'] = np.arange(145, 145 + len(future_dates))
future_df.head()

نمونه ردیف‌ها از  future_df:

اکنون می‌توانیم از future_df برای انجام پیش‌بینی استفاده کنیم:

predictions_future = predict_model(best, data=future_df)
predictions_future.head()

خروجی تابع ()predictions_future.head :

حالا می‌توانیم نتایج را رسم کنیم:

concat_df = pd.concat([data, predictions_future], axis=0)
concat_df_i = pd.date_range(start='1949-01-01', end='1965-01-01', freq='MS')
concat_df.set_index(concat_df_i, inplace=True)
fig = px.line(concat_df, x=concat_df.index, y=["Passengers", "Label"], template='plotly_dark')
fig.show()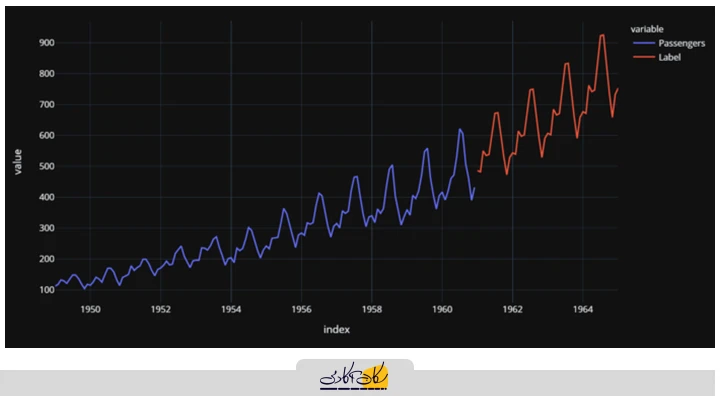

نکته مهم:
هر زمان با یک سری زمانی تک‌متغیره روبه‌رو باشید، می‌توانید آن را به یک مسئله رگرسیون تبدیل کرده و مانند مثال فوق حل کنید. اما باید در مورد اعتبارسنجی محتاط باشید. نمی‌توانید از اعتبارسنجی تصادفی بر روی مدل‌های سری زمانی استفاده کنید باید از روش‌های مناسب برای سری زمانی بهره ببرید. در این مثال،  PyCaret  از TimeSeriesSplit کتابخانه scikit-learn استفاده کرده است.

فریم‌ورک‌های پایتونی برای پیش‌بینی سری زمانی

1. Facebook Prophet

Prophet یک نرم‌افزار متن‌باز است که توسط تیم Core Data Science شرکت فیسبوک منتشر شده و می‌توان آن را از طریق CRAN و PyPI دانلود کرد.
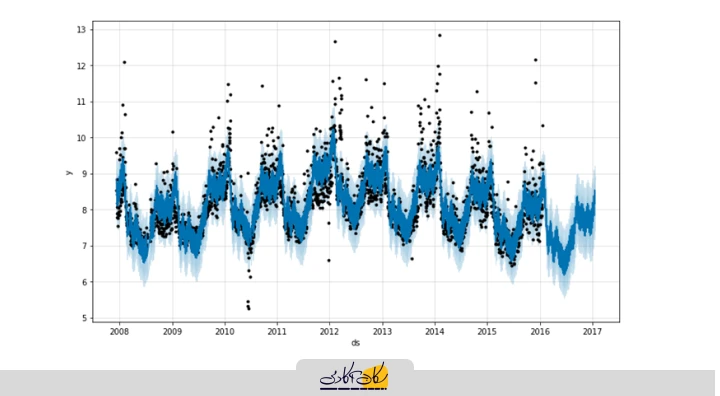
Prophet روشی برای پیش‌بینی داده‌های سری زمانی مبتنی بر یک مدل جمع‌شونده (Additive Model) است، که در آن، روندهای غیرخطی با فصلی‌های سالانه، هفتگی و روزانه به‌همراه اثرات رویدادهای خاص (مثلاً تعطیلات) برازش می‌شوند. این روش زمانی بهترین عملکرد را دارد که سری زمانی دارای اثرات فصلی قوی و چندین فصل داده‌ی تاریخی باشد.
Prophet در برابر داده‌های گمشده مقاوم است و در برابر تغییرات در روند و نقاط پرت معمولاً عملکرد خوبی نشان می‌دهد. برای یادگیری بیشتر، به این لینک مراجعه کنید: Python API

2. sktime

sktime یک فریمورک پایتون متن‌باز و یکپارچه برای یادگیری ماشین با داده‌های سری زمانی است. این ابزار بستری انعطاف‌پذیر و ماژولار را برای طیف گسترده‌ای از وظایف یادگیری ماشین بر روی سری‌های زمانی فراهم می‌کند. این کتابخانه با واسط‌های سازگار با scikit-learn و ابزارهای ترکیب مدل، قصد دارد اکوسیستمی قابل استفاده‌تر و یکپارچه‌تر ایجاد کند.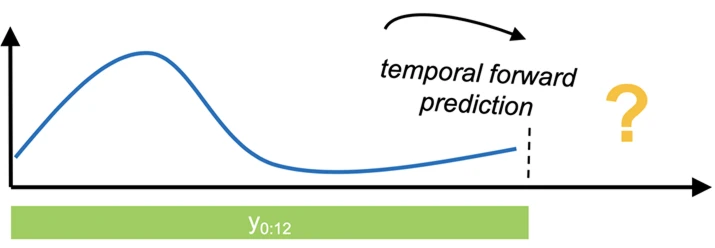

برای آشنایی بیشتر باsktime ، این لینک را بررسی کنید. 

3. pmdarima

pmdarima یک کتابخانه آماری است که هدف آن پر کردن خلأ موجود در قابلیت‌های تحلیل سری زمانی در پایتون است. این کتابخانه قابلیت‌های زیر را فراهم می‌کند:

• معادل تابع auto.arima در R
• مجموعه‌ای از آزمون‌های آماری برای ایستایی و فصلی بودن
• تجزیه فصلی سری‌های زمانی
• امکانات اعتبارسنجی متقابل (Cross-validation)
• مجموعه‌ای غنی از مجموعه داده‌های سری زمانی داخلی برای نمونه‌سازی و مثال‌ها

برای یادگیری بیشتر درباره pmdarima، به این صفحه مراجعه کنید.

4. Kats

Kats یک پروژه متن‌باز دیگر از فیسبوک است که توسط تیم زیرساخت علم داده (Infrastructure Data Science) ارائه شده و از طریق PyPI قابل دانلود است. Kats یک جعبه‌ابزار قدرتمند و کارآمد برای تحلیل داده‌های سری زمانی در پایتون است. این ابزار با ارائه یک فریمورک سبک، ساده و انعطاف‌پذیر، کاربران را قادر می‌سازد تا انواع تحلیل‌های سری زمانی را به‌راحتی انجام دهند. هدف Kats ایجاد یک "مرکز جامع" برای تحلیل سری زمانی است که شامل امکانات زیر می‌شود:

• تشخیص (Detection): شناسایی تغییرات، الگوها و نقاط عطف در سری زمانی.
• پیش‌بینی (Forecasting): ارائه مدل‌های متنوع برای پیش‌بینی مقادیر آینده سری زمانی.
• استخراج و تعبیه ویژگی‌ها (Feature Extraction/Embedding): استخراج ویژگی‌های مرتبط از داده‌های سری زمانی برای تحلیل‌های پیشرفته.
• تحلیل چندمتغیره (Multivariate Analysis): تحلیل روابط بین چندین سری زمانی.

Kats به‌دلیل سهولت استفاده، انعطاف‌پذیری بالا و تعمیم‌پذیری، گزینه‌ای ایده‌آل برای دانشمندان داده و تحلیلگران در تحلیل سری‌های زمانی است و برای طیف وسیعی از کاربردها، از پیش‌بینی فروش گرفته تا تحلیل رفتار کاربران، مناسب است. 

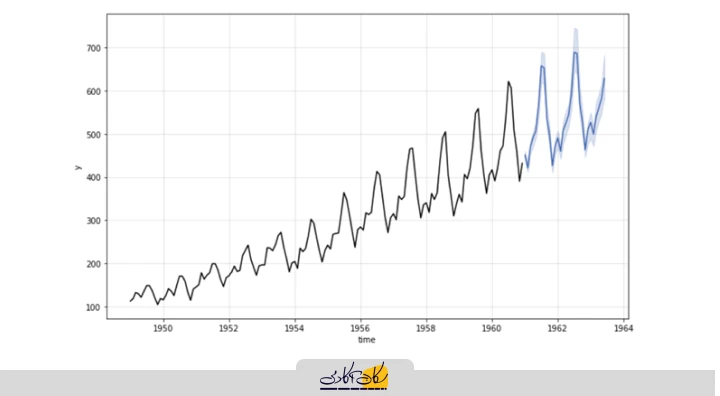
برای یادگیری بیشتر درباره KATS، این لینک را ببینید. 

5. Orbit

Orbit یک پروژه متن‌باز فوق‌العاده از Uber است و یک کتابخانه پایتون برای پیش‌بینی بیزی (Bayesian) در سری‌های زمانی محسوب می‌شود. Orbit یک واسط آشنا و شهودی از نوع initialize-fit-predict برای وظایف سری زمانی ارائه می‌دهد و در پشت صحنه از زبان‌های برنامه‌نویسی احتمالاتی استفاده می‌کند.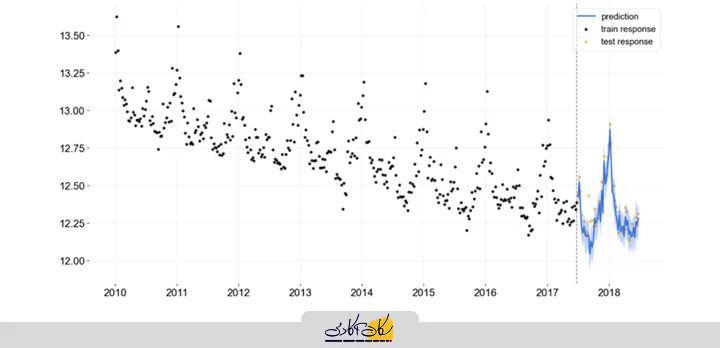

برای یادگیری بیشتر درباره Orbit، این لینک را بررسی کنید.

6. PyCaret

PyCaret یک کتابخانه متن‌باز و کم‌کدنویسی (Low-code) یادگیری ماشین در پایتون است که فرآیندهای یادگیری ماشین را خودکار می‌کند. با PyCaret، زمان کمتری صرف کدنویسی می‌کنید و زمان بیشتری را صرف تحلیل می‌کنید. با استفاده از آن می‌توانید مدل خود را آموزش دهید، تحلیل کنید، با سرعت بیشتری تکرار کنید و حتی فوری آن را به شکل یک REST API مستقر کنید یا یک اپلیکیشن مبتنی بر یادگیری ماشین با رابط گرافیکی ساده ایجاد کنید، و همه این‌ها از طریق Notebook محبوبتان قابل انجام است.

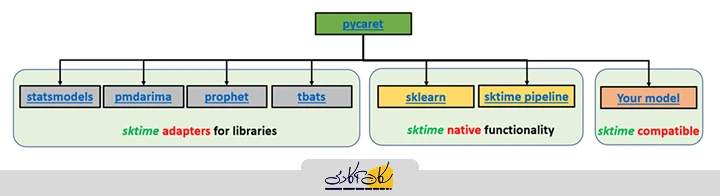
 در ادامه، مثالی از یک فرآیند کامل پیش‌بینی سری زمانی به صورت انتها به انتها (End-to-End) با استفاده از کتابخانه PyCaret ارائه شده است.

مثالی جامع از فرایند انتها-به-انتها (End-to-End)

ماژول سری زمانی PyCaret در حالت بتا قرار دارد و می‌توانید با دستور زیر نصبش کنید:

pip install pycaret-ts-alpha

 1.مجموعه‌داده

در اینجا ما از مجموعه داده‌ای که شامل داده‌های خطوط هوایی است استفاده می‌کنیم، این داده‌ها در مخزن داده PyCaret نیز موجود هستند:

from pycaret.datasets import get_data
data = get_data('airlineer')

Period
1949-01    112.0
1949-02    118.0
1949-03    132.0
1949-04    129.0
1949-05    121.0
Freq: M, Name: Number of airline passengers, dtype: float64

2.تصویرسازی داده‌ها

data.plot()

3. راه‌اندازی آزمایش (Setup)  

در PyCaret، شروع آزمایش با تابع setup  انجام می‌شود. این تابع تمام مراحل پیش‌پردازش داده، تقسیم داده به آموزش/آزمایش، استراتژی اعتبارسنجی متقابل و چند کار دیگر را مدیریت می‌کند:

from pycaret.time_series import *
s = setup(data, session_id = 123)

4.تحلیل اکتشافی داده‌ها (EDA)

هنگام تحلیل داده‌های سری زمانی تک‌متغیره، می‌توانید تست‌های آماری مختلفی انجام دهید. تابع ()check_stats در PyCaret این کار را برای شما ساده می‌کند:

check_stats()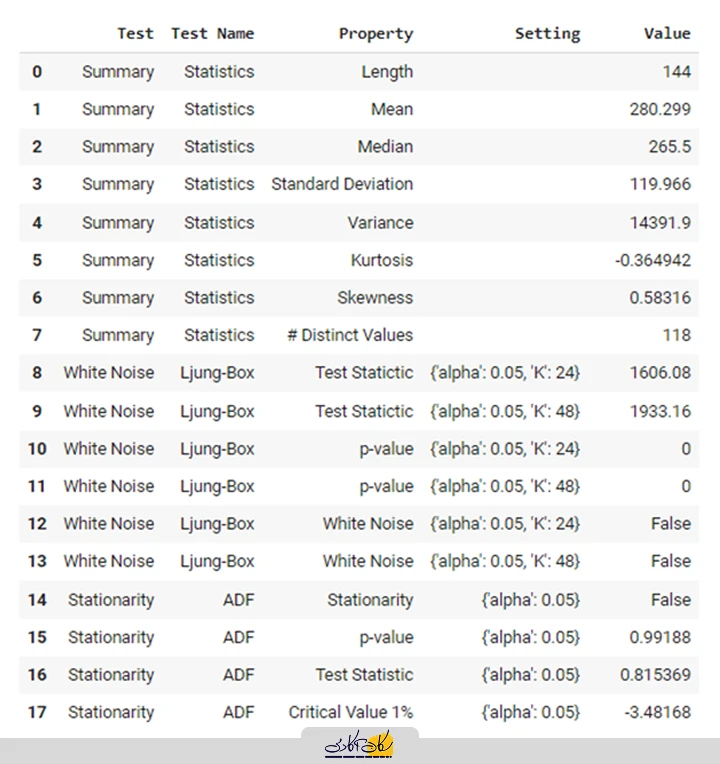

همچنین می‌توانید سری زمانی را به مولفه‌های روند، فصلی و نویز تجزیه کنید:

plot_model(plot='decomp_classical')

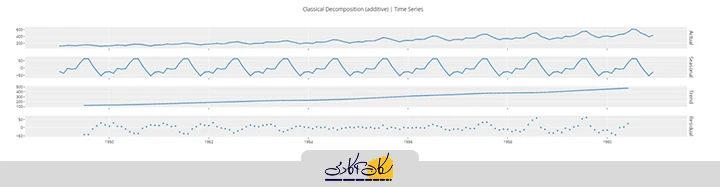
6.آموزش و انتخاب مدل

برای آموزش مدل‌های متعدد و انتخاب یکی از آن‌ها، تنها یک خط کد کافی است:

best = compare_models()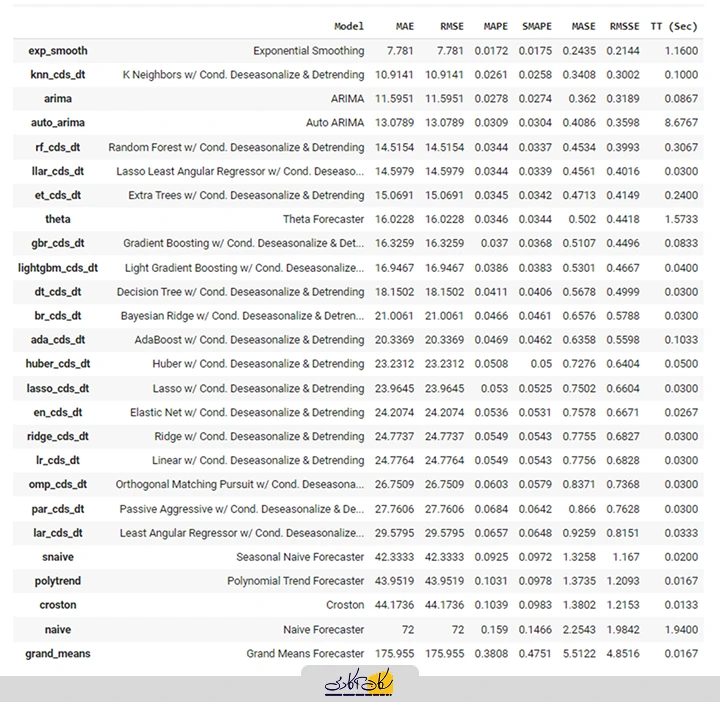

بیش از 25 مدل را با استفاده از استراتژی اعتبارسنجی مناسب سری زمانی آموزش داده و فهرستی از مدل‌ها را بر اساس عملکرد از بهتر به بدتر ارائه کرده است. برای این مجموعه‌ داده، بهترین مدل بر اساس این آزمایش هموارسازی نمایی (Exponential Smoothing) با MAE حدود 7.781 است.

7.تحلیل مدل

قبل از استقرار مدل برای تولید پیش‌بینی، می‌توانیم چند نمودار تحلیلی را مشاهده کنیم:

plot_model(best, plot='forecast', data_kwargs={'fh': 24})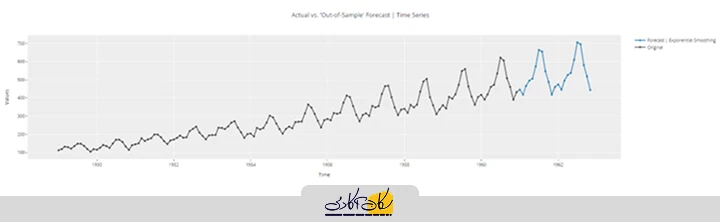

plot_model(best, plot='residuals')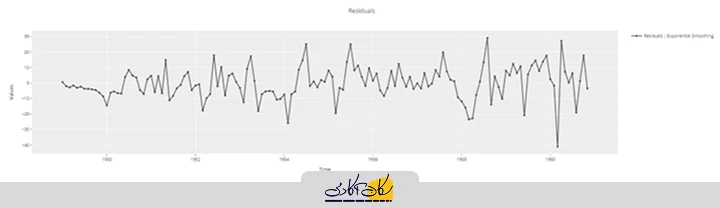

plot_model(best, plot='insample')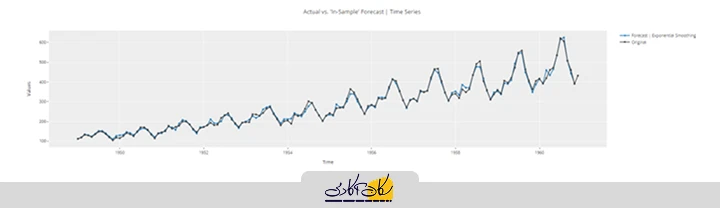

پیش‌بینی درون نمونه به تخمین مقادیر داده‌هایی اشاره دارد که مدل بر اساس آن‌ها آموزش دیده است. معمولاً برای ارزیابی دقت مدل در همان بازه زمانی که داده‌ها از آن استخراج شده‌اند، استفاده می‌شود.

8.استقرار مدل

اکنون می‌توانیم مدل را نهایی کرده و برای استفاده‌های بعدی ذخیره کنیم:

final_best = finalize_model(best)
save_model(final_best, 'my_best_model')

Transformation Pipeline and Model Successfully Saved
(ExponentialSmoothing(damped_trend=False, initial_level=None,
    initial_seasonal=None, initial_trend=None,
    initialization_method='estimated', seasonal='mul', sp=12,
    trend='add', use_boxcox=None), 'my_best_model.pkl')

برای بارگذاری مدل و تولید پیش‌بینی برای داده‌های آینده:

loaded_model = load_model('my_best_model')
predict_model(loaded_model, fh = 48)

 جمع‌بندی

پیش‌بینی سری زمانی مهارتی بسیار کاربردی است زیرا بسیاری از مسائل واقعی در صنایع مختلف ماهیت سری زمانی دارند. برای مثال از پیش‌بینی هواشناسی، اقتصاد، سلامت و امور مالی گرفته تا خرده‌فروشی، کسب‌وکار، مطالعات محیطی و اجتماعی و موارد دیگر.

در اصل، هر داده تاریخی با فواصل منظم را می‌توان با روش‌های تحلیل سری زمانی بررسی کرد تا یک وظیفه پیش‌بینی شکل بگیرد که از داده‌های تاریخی می‌آموزد و آینده را پیش‌بینی می‌کند. به طور خلاصه، همانظور که گفته شد، سه دسته اصلی برای پیش‌بینی سری زمانی وجود دارد:

1. مدل‌های آماری: هموارسازی نمایی، ARIMA، SARIMA، TBATS و ...
2. یادگیری ماشین: رگرسیون خطی، XGBoost، جنگل تصادفی و ...
3. یادگیری عمیق: RNN، LSTM