الگوریتم Dynamic programming به همراه مثال و تمرین

این مقاله قسمت جدیدی از سری مقاله های 6 الگوریتم جادویی دنیای برنامه نویسی است. در این بخش به یکی از جذاب ترین و حرفه ای ترین تکنیک های الگوریتمی با عنوان dynamic programming (DP) یا برنامه نویسی پویا رسیدیم. طبق قرار قبلی، این سری مقاله ها شامل 6 بخش زیر است که می توانید مقاله های قبلی را هم مطالعه بفرمایید.

الگوریتم Brute Force به همراه مثال و تمرین
الگوریتمGreedy به همراه مثال و تمرین
الگوریتمRecursive به همراه مثال و تمرین
الگوریتم Backtracking به همراه مثال و تمرین
الگوریتم Dynamic programming به همراه مثال و تمرین
الگوریتمRandomized به همراه مثال و تمرین

الگوریتم Dynamic Programming چیست؟

برنامه نویسی پویا که به اختصار به آن DP هم گفته می شود، تکنیک الگوریتمی ای برای حل مسائل بهینه سازی است و این کار را با شکستن یک مسئله ی بزرگ به مسائل کوچکتر و ساده تر انجام می دهد. در اصل DP یک بهینه سازی روی روش بازگشت (Recursion) است.

برای حل اینگونه مسائل، همانطور که در الگوریتم های Backtracking و Recursive هم مشاهده کردید، راه حل بهینه ی مسئله ی اصلی، به راه حل های بهینه برای مسائل کوچکتر بستگی دارد.

ایده ی پشت این الگوریتم که باعث بهینه سازی توابع بازگشتی می شود خیلی ساده است. در واقع در این الگوریتم، باید نتایج بدست آمده از مسائل کوچکتر را نگه داریم تا مجبور نباشیم، آنها را چندین بار محاسبه کنیم.

برای درک بهتر، با مثال سری فیبوناچی ادامه خواهیم داد. همانطور که می دانید، سری فیبوناچی، مجموعه ای از اعداد است که هر عضو آن، حاصل جمع دو عضو قبلی است.

... ,13 ,8 ,5 ,3 ,2 ,1 ,1 ,0

اگر بخواهیم عدد nام در سری فیبوناچی را بدانیم، لازم است از شبه کد زیر استفاده کنیم.

Fib(n) = Fib(n-1)+Fib(n-2) , for n>1

همانطوری که مشاهده می کنید، برای حل مسئله ی بزرگ Fib(n) نیاز است، دو مسئله ی کوچکتر Fib(n-1) و Fib(n-2) را حل کنیم. و این نشانه ایست که به ما می گوید، می توانیم برای حل این مسئله از DP بهره ببریم.

مسائل کوچکتر، درواقع نسخه ی کوچک شده ای از مسئله ی اصلی هستند. هر مسئله ای شامل مسائل کوچکتری می شود که پیدا کردن پاسخ آنها، به پیدا کردن مسئله ی اصلی منجر می شود. برای مثال، در ادامه سری عددی فیبوناچی، برای عدد 4 را مشاهده می کنید که چطور به مسائل کوچکتری تبدیل شده اند:

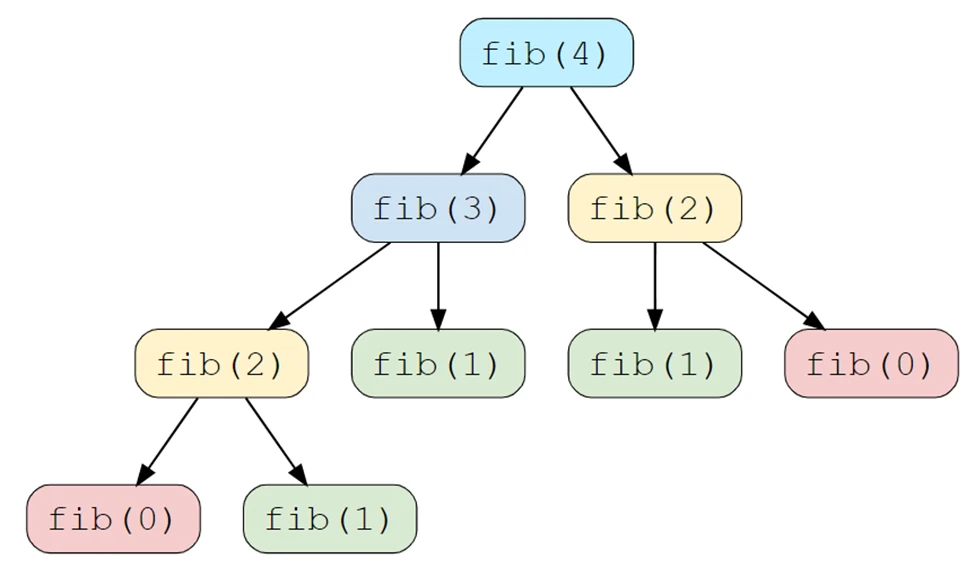
در خت بازگشتی محاسبه ی فیبوناچی برای عدد 4

همانطور که مشاهده می کنید، دوباره کاری در حل مسئله های کوچکتر، به وضوح قابل مشاهده است. برای مثال fib(2) دوبار و fib(1) سه بار محاسبه شده است. که این موضوع باعث افزایش میزان پیچیدگی زمانی (نماد O بزرگ) الگورتیم شما به صورت نمایی (O(c^n)) می شود. درحالی که اگر از DP بهره ببریم، پیچیدگی زمانی الگوریتم ما به صورت خطی (O(n)) خواهد بود.

تکه کد زیر با الگوریتم بازگشتی مسئله ی سری فیبوناچی را حل کرده است. که از نظر معیار پیچیدگی زمانی، بهینه نیست و به صورت نمایی این شاخص افزایش پیدا می کند.

int fib(int n){
    if(n <= 1)
        return n;
    return fib(n-1) + fib(n-2);
}

همین مسئله را می توان با الگوریتم DP به گونه ای نوشت که باعث شود پیچیدگی زمانی، به بهینه ترین حالت ممکن، بهبود یابد.

f[0] = 0;
f[1] = 1;

for (i=2 ; i <= n; i++){
    f[i] = f[i-1]+ f[i-2];
}

return f[n]

برای اینکه تفاوت عملکرد دو الگوریتم بالا را با هم مقایسه کنید، نمودارهای زیر، که نمایشی از وضعیت پیچیدگی زمانی است را با هم مقایسه کنید. (الگوریتم اول O(2^n) و الگوریتم دوم O(n) می باشد)

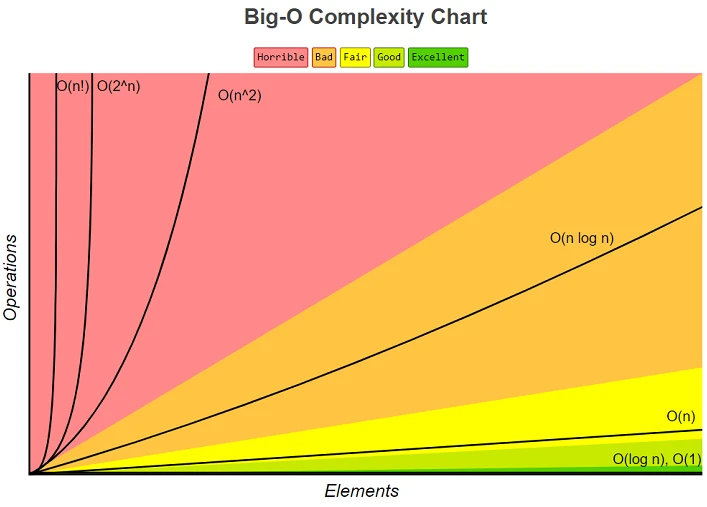
روش های Dynamic Programming

برنامه نویسی پویا، دو روش را برای حل مسائل پیشنهاد می دهد:

روش یادداشت کردن یا Memoization

در این رویکرد، ما با حل مسائل کوچکتر و ذخیره ی آنها در Cache، جهت جلوگیری از تکرار محاسبه ی آنها، سعی می کنیم به راه حل مسئله ی اصلی برسیم. به این روش Memoization (یادداشت کردن) هم گفته می شود. یادداشت کردن تکنیکی است برای "به خاطر سپردن" نتیجه محاسبات، تا برای صرفه جویی در زمان، به جای محاسبه ی مجدد، در دفعه های بعدی از همان نتایج استفاده شود.

بیایید حل مسئله ی فیبوناچی را با این رویکرد در زبان جاوااسکریپت ببینیم:

const calculateFibonacci = function(n) {
    const memoize = [];
 
    function fib(n) {
      if (n < 2) return n;
 
      // if we have already solved this subproblem, simply return the result from the cache
      if (memoize[n]) return memoize[n];
 
      memoize[n] = fib(n - 1) + fib(n - 2);
      return memoize[n];
    }
 
    return fib(n);
  };
 
  console.log(`5th Fibonacci is ---> ${calculateFibonacci(5)}`);
  console.log(`6th Fibonacci is ---> ${calculateFibonacci(6)}`);
  console.log(`7th Fibonacci is ---> ${calculateFibonacci(7)}`);

روش جدول بندی یا Tabulation

روش جدول بندی، برعکس رویکرد یادداشت برداری است و از بازگشت مجدد جلوگیری می کند. در این رویکرد، ما مشکل را «از پایین به بالا» حل می‌کنیم (یعنی ابتدا، حل تمام مسائل کوچکتر مرتبط). در این روش ما باید یک جدول n بعدی را پرکنیم و با توجه به نتایج موجود در جدول، مسئله ی اصلی حل می شود.

بیایید از این روش جدول بندی برای مثال خودمان که حل سری عددی فیبوناچی است، استفاده کنیم. با توجه به اینکه هر عددی در سری فیبوناچی، مجموع دو عدد قبلی اش است، می خواهیم جدول مان را پر کنیم.

const calculateFibonacci = function(n) {
  const dp = [0, 1];
  for (let i = 2; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2];
  }
  return dp[n];
};

console.log(`5th Fibonacci is ---> ${calculateFibonacci(5)}`);
console.log(`6th Fibonacci is ---> ${calculateFibonacci(6)}`);
console.log(`7th Fibonacci is ---> ${calculateFibonacci(7)}`);

در این مقاله با Dynamic Programming و دو روش اصلی برای حل مسائلی که به الگوریتم DP نیاز دارند، یعنی Memoization و Tabulation آشنا شدیم.

یادتان هست در تمرین مقاله ای که الگوریتم Greedy را برایتان توضیح دادم، گفتم این تمرین در دنیای برنامه نویسی به عنوان مسئله ی کوله پشتی یا Knapsack یا Backpack Problem معروف است؟

در مسئله ی کوله پشتی، از ما خواسته می شود که بر اساس وزن و ارزش، N کالا را در یک کوله پشتی با ظرفیت C قرار بدهیم. که البته از هر کالا هم، فقط یک مورد می توانیم در کوله پشتی قرار دهیم. هدف نهایی هم این است که ارزشمندترین کوله پشتی را در انتها جمع کنیم.

حالا به عنوان تمرین برای الگوریتم Dynamic Programming، همان تمرین موجود در مقاله ی Greedy را با استفاده از این الگوریتم باز نویسی کنید.

امیدوارم با آموختن این الگوریتم و استفاده کردن از آن، به برنامه نویس های حرفه ای تری تبدیل شوید.