الگوریتم Backtracking (عقب گرد) چیست؟
الگوریتم Backtracking (عقب گرد) یکی از الگوریتم هایی هست که ذهن آدم را ورزش می دهد و از آلزایمر در سنین بالا جلوگیری می کند😉. در این الگوریتم، با یک گزینه ی ممکن از تعداد زیادی گزینه ی موجود شروع می کنیم و سعی می کنیم مشکل را حل کنیم. اگر بتوانیم مشکل را با گزینه ی انتخاب شده حل کنیم، راه حل را چاپ می کنیم در غیر این صورت به عقب برمی گردیم و گزینه دیگری را انتخاب می کنیم و سعی می کنیم آن را حل کنیم.
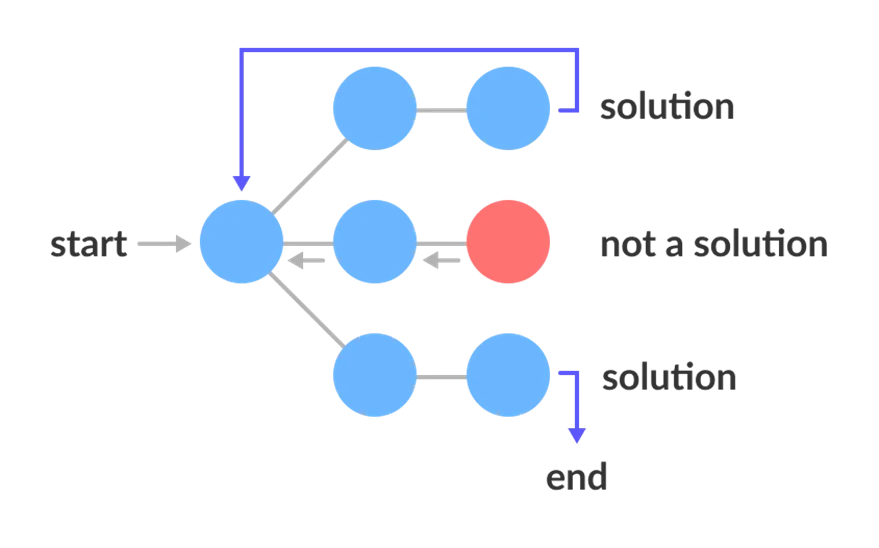
شاید بتوان این الگوریتم را به گونه ای ترکیبی از ایده های Brute Force و Recursive دانست. چرا که در این الگوریتم، مانند Brute Force تمام گزینه های احتمالی بررسی می شود و البته ماننده Recursive هم با فراخوانی مجدد یک تابع، بارها و بارها یک مسیر مشخص طی می شود.
برای این که بهتر، این موضوع را درک کنید بیایید روی دو مثال باهم پیش برویم. اولین مثال کمی ساده تر است و به توضیح غیر کدی خلاصه می شود و دومین مثال مان حل مسئله ی N Queen خواهد بود که در این مثال تا مرحله ی کد نویسی هم پیش می رویم.
فرض کنید در یک کلاس، دو پسر و یک دختر داریم. قرار است این سه نفر روی یک نیمکت بنشینند و تنها محدودیت مان این است که دو پسر باید حتما کنار هم باشند. برای این موضوع 6 = !3 حالت می توانیم داشته باشیم. بیاید ابتدا حالت های مختلف را بدون در نظر گرفتن محدودیت ببینیم:

با توجه به محدودیتی که در صورت مسئله داشتیم، حالت های سه و چهار نامناسب است. پس در نتیجه تابع ما باید بتواند همه ی حالت های بالا به جز دو حالت نامناسب را برگرداند.
الگوریتم عقبگرد یا Backtracking را می توان به صورت زیر در قالب یک شبه کد نمایش داد:
Backtrack(x)
if x is not a solution
return false
if x is a new solution
add to list of solutions
backtrack(expand x)توجه داشته باشید که در الگوریتم Backtracking ما به یک راه حل نمی رسیم و به دنبال راه حل های متعددی می گردیم.
💎 قبل از اینکه به مثال بعدی برویم، خودتان با توجه به شبه کدی که معرفی شد و مسئله ای که مطرح شد، کدی بنویسید که راه حل های مسئله را پیشنهاد بدهد.
مسئله ی N Queen
یکی از مسئله های خیلی جالب که با الگوریتم عقبگرد یا Backtracking حل می شود مسئله ی N وزیر یا N ملکه (N Queen Problem) است. همانطور که می دانید، در بازی شطرنج ملکه می تواند به هر تعداد خانه در ستون، سطر یا قطری که در آن هست حرکت کند.
مسئله ی N ملکه اینطور است که قصد داریم N ملکه را در یک صفحه ی شطرنج N*N به گونه ای قرار دهیم که هیچکدام از آنها دیگری را تهدید نکند. یعنی هیچ کدام از آنها در سطر ، ستون یا قطر دیگری قرار نداشته باشد. مثلا مطرح می شود که می خواهیم 8 ملکه را در یک صفحه ی شطرنج 8*8 به گونه ای قرار دهیم که هیچ یک از آنها دیگری را تهدید نکند.

⚠ نمی دانم چرا ما به این مهره ی شطرنج همیشه وزیر می گفتیم، ولی با توجه به اینکه دقیقا عنوان این مسئله N Queen است، من هم در این مقاله به این مهره، ملکه خواهم گفت. اگر کسی می داند چرا ما به این مهره وزیر می گفتیم، توی کامنت ها دلیلش را به من هم بگوید.😏
تصویرمتحرک زیر مراحل حل این مسئله برای 8 ملکه را نشان می دهد:

در ادامه قصد داریم این مسئله را با 4 ملکه بررسی کنیم، الگوریتم آن را طراحی کرده و در نهایت پیاده سازی کنیم. انتظار می رود خروجی این الگوریتم، ماتریکسی مانند ماتریکس زیر باشد که به عنوان راه حل مسئله ی 4 ملکه بدست آمده است. در این ماتریکس محل قرار گیری هر ملکه با عدد 1 پر شده است.
{ 0, 1, 0, 0}
{ 0, 0, 0, 1}
{ 1, 0, 0, 0}
{ 0, 0, 1, 0}
ماتریکس بالا در واقع بیان کامپیوتری تصویر زیر می باشد:

⛔ پیشنهاد میکنم قبل از اینکه راه حل مسئله را در ادامه مشاهده کنید، تلاش کنید خودتان این مسئله را حل کنید.
راه حل مسئله ی N Queen با الگوریتم Backtracking
ایده ای که برای حل این مسئله دنبال می کنیم، به این شکل است که ابتدا ملکه ها را یکی بعد از دیگری روی ستون های مختلف قرار می دهیم. این کار را از ستون سمت چپ شروع می کنیم. وقتی هر ملکه را روی ستونی قرار دادیم، بررسی می کنیم که آیا با ملکه های قبلی که قرار داده شده اند برخوردی دارد یا خیر. حالا که ستون مناسب را پیدا کردیم، باید به دنبال ردیف مناسب هم بگردیم. برای این کار، در هر ردیفی که ملکه را قرار دادیم، باید بررسی کنیم که با ملکه های قبلی برخورد نداشته باشد. حالا این ستون و ردیف را به عنوان بخشی از جواب علامت گذاری کنید. اگر چنین ردیفی را به دلیل برخورد ملکه با ملکه های قبلی پیدا نکردیم، باید False برگردانیم و عقبگرد کنیم و از ابتدا حالت ها را بررسی کنیم.
الگوریتم مسئله ی N Queen با Backtracking
- از سمت چپ ترین ستون شروع می کنیم.
- اگر همه ی ملکه ها در جای درست قرار گرفتند، True را برمی گردانیم.
- تمام سطرهای ستون فعلی را امتحان می کنیم: هر کدام از کارهای زیر را برای هر سطر انجام می دهیم.
- اگر ملکه را بتوان با خیال راحت در این ردیف قرار داد سپس این [ردیف، ستون] را به عنوان بخشی از راه حل علامت گذاری می کنیم و به صورت بازگشتی بررسی خواهیم کرد که آیا محلی که ملکه در آن قرار گرفته است، منجر به یک راه حل می شود یا خیر.
- اگر [ردیف]، ستون[ ای که ملکه در آن قرار گرفته است، منجر به پاسخ می شود، True را برمی گردانیم.
- اگر محل قرار گیری ملکه منجر به نتیجه نشد، ابتدا ]ردیف، ستون[ علامت گذاری شده را از دسته ی راه حل ها خارج می کنیم، سپس عقبگرد کرده و به مرحله ی a برمی گردیم تا ردیف های دیگر را امتحان کنیم.
- اگر همه ی ردیف ها را امتحان کردیم و هیچ کدام کار نکرد، False را برمی گردانیم و عقبگرد کرده تا ملکه های قبلی را دوباره جانمایی کنیم.
پیاده سازی الگوریتم Backtracking یا عقبگرد
در ادامه، پیاده سازی الگوریتم بالا را با زبان Python3 مشاهده می کنید:
ابتدا تابعی را برای نمایش راه حل تعریف می کنیم:
global N
N = 4
def printSolution(board):
for i in range(N):
for j in range(N):
print (board[i][j], end = " ")
print()در این مرحله به تابعی احتیاج داریم که بررسی کند، آیا ملکه می تواند در خانه ی ]ردیف[ و ]ستون[ بدست آمده قرار بگیرد یا خیر؟ توجه داشته باشید ما برای جانمایی ملکه ها، از چپ به راست حرکت کردیم. در نتیجه، زمانی که این تابع فراخوانی می شود، ملکه های قبلی در ستون های قبل از ستون فعلی (یعنی ستون های سمت چپ ستون فعلی) قرار گرفته اند. در نتیجه ما فقط نیاز داریم ستون های سمت راست را بررسی کنیم.
def isSafe(board, row, col):
# Check this row on left side
for i in range(col):
if board[row][i] == 1:
return False
# Check upper diagonal on left side
for i, j in zip(range(row, -1, -1),
range(col, -1, -1)):
if board[i][j] == 1:
return False
# Check lower diagonal on left side
for i, j in zip(range(row, N, 1),
range(col, -1, -1)):
if board[i][j] == 1:
return False
return True
def solveNQUtil(board, col):
# base case: If all queens are placed
# then return true
if col >= N:
return True
# Consider this column and try placing
# this queen in all rows one by one
for i in range(N):
if isSafe(board, i, col):
# Place this queen in board[i][col]
board[i][col] = 1
# recur to place rest of the queens
if solveNQUtil(board, col + 1) == True:
return True
# If placing queen in board[i][col
# doesn't lead to a solution, then
# queen from board[i][col]
board[i][col] = 0
# if the queen can not be placed in any row in
# this colum col then return false
return Falseدر مرحله ی بعدی باید تابع اصلی را که مسئله ی N Queen را با استفاده از الگوریتم Backtracking حل می کند، بنویسیم. درواقع کار اصلی برای حل مسئله در این تابع، توسط تابع solveNQUtil که در بالا نوشتیم انجام می شود. این تابع اگر نتواند برای ملکه جای مناسبی پیدا کند False را برمی گرداند و در غیر این صورت True را به عنوان خروجی اجرای خودش برمی گرداند.
def solveNQ():
board = [ [0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0] ]
if solveNQUtil(board, 0) == False:
print ("Solution does not exist")
return False
printSolution(board)
return Trueدر نهایت هم که اجرای کد حل مسئله ی N Queen را داریم:
solveNQ()تمرین الگوریتم Backtracking
نقشه ی دفتر سکان آکادمی به شکل زیر است:
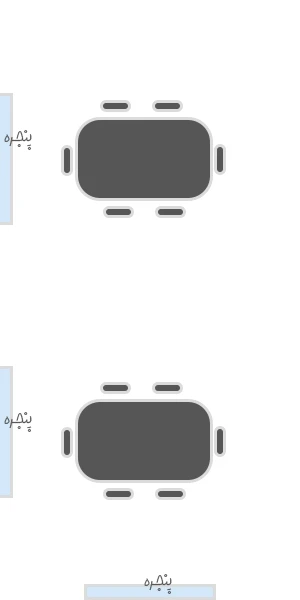
همانطور که در تصویر هم مشخص است سه پنجره وجود دارد و چهار صندلی که در کنار پنجره ها قرار دارند. دور هر میز هم 6 نفر می توانند بنشینند. سه همکار خانم داریم که در فرم انتظارهای شان از محیط کار، نشستن در کنار پنجره را خواسته بودند. همچنین همکاران خانم مان هم نباید کنار هم بنشینند. لطفا با الگوریتم Backtracking، تکه کدی را بنویسید که راه حل هایی را برای این نیازمندی ارائه بدهد.
توجه داشته باشید که هرکدام از میز ها را می توانید به عنوان یک آرایه (یا صندلی های هر دو میز را به عنوان یک آرایه) در نظر بگیرید و محل نشستن خانم های تیم سکان آکادمی را با عدد 1 و بقیه ی صندلی ها را با عدد 0 پرکنید. در کامنت کدتان هم شماره ی ردیف و ستون صندلی هایی که در کنار پنجره هستند را مشخص کنید.
منتظر دریافت پاسخ های شما هستم.
امیدوارم به عنوان یک برنامه نویس زندگی خوبی با الگوریتم ها داشته باشید 😉