در مقاله ی قبلی از سری مقالات 6 الگوریتم جادویی دنیای برنامه نویسی، درباره ی الگوریتم Brute Force صحبت کردیم. در این قسمت قصد داریم به دومین الگوریتم جادویی بپردازیم که الگوریتم محبوب و کار راه انداز Greedy است.
الگوریتم Greedy، یک الگوریتم ساده و شهودی است که در مسائل بهینه سازی استفاده می شود. این الگوریتم در هر مرحله، انتخاب بهینه را انجام می دهد تا بتواند راه بهینه برای حل کل مسئله را بیابد. در سایت های فارسی، نام این الگوریتم را حریصانه ترجمه کرده اند ولی من ترجیح می دهم با همان Greedy ادامه بدهم. الگوریتمهای Greedy در برخی مشکلات کاملاً موفق هستند، مانند کدگذاری هافمن (Huffman encoding) که برای فشردهسازی دادهها استفاده میشود، یا الگوریتم Dijkstra که برای یافتن کوتاهترین مسیر از طریق یک گراف استفاده میشود.
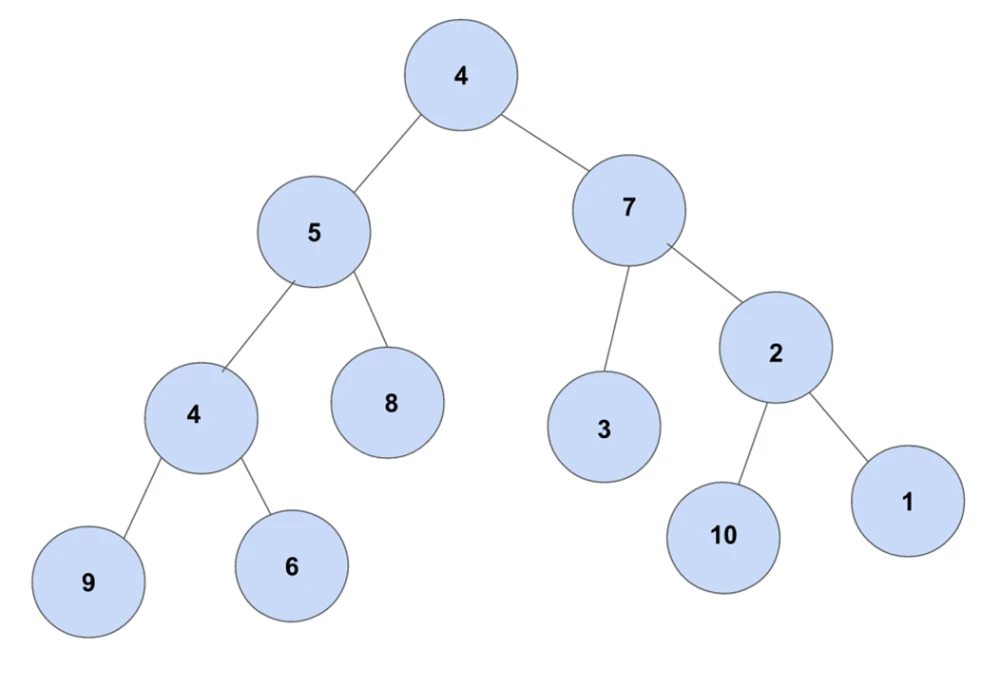
با این حال، در بسیاری از مشکلات، یک استراتژی Greedy راه حل بهینه را پیدا نمی کند. به عنوان مثال، در انیمیشن زیر، الگوریتم Greedy به دنبال یافتن مسیری است که جمع گره های آن بیشینه (Maximum) باشد. با توجه به این که، این کار را با انتخاب بزرگترین عدد موجود در هر مرحله انجام می دهد، نمی تواند بزرگترین مجموع را بیابد، زیرا تنها بر اساس اطلاعاتی که در هر مرحله دارد، بدون توجه به داده های کلی تصمیم می گیرد.
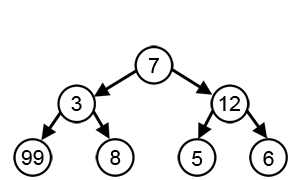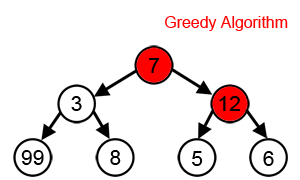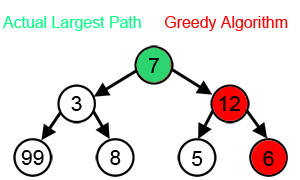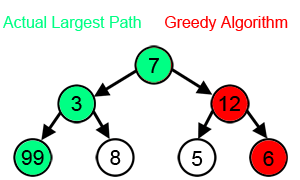
همانطور که در تصویر بالا می بینید، با هدف رسیدن به بزرگترین مجموع، در هر مرحله، الگوریتم Greedy، گزینه ای را انتخاب می کند که به نظر می رسد بهترین انتخاب در رسیدن به هدف است، بنابراین در مرحله دوم به جای 3، 12 را انتخاب می کند و به بهترین راه حل که شامل 99 است نمی رسد.
برای تولید یک برنامه بر اساس الگوریتم Greedy، شما نیاز دارید مسئله را به یک تعدادی مسئله ی کوچکتر تبدیل کنید. برای مثال کوتاه ترین مسیر و یا بیشترین مجموع را که هدف کلی مسئله است، به مسائل کوچکتری مثل اینکه بین دو نقطه ی پیش رو کدام یک کوتاه تر است و یا کدامیک عدد بزرگتری است, انتخاب را انجام دهید. سپس همین کار را آن قدر تکرار کنید تا کلیه ی داده های موجود در مسئله را بررسی کرده و بهترین انتخاب ها را در هر مرحله داشته باشید.
الگوریتم Greedy دارای 5 جز است:
- یک مجموعه از کاندیداهایی که ما سعی می کنیم از بین آنها راه حلی را پیدا کنیم.
- یک تابع انتخاب که به انتخاب بهترین کاندیدای ممکن کمک می کند.
- یک تابع امکان سنجی که به تصمیم گیری در مورد استفاده از کاندیدای مورد نظر برای یافتن راه حل کمک می کند.
- یک تابع هدف که به یک راه حل ممکن یا به یک راه حل جزئی مقدار می دهد.
- تابع راه حل که می گوید چه زمانی راه حلی برای مشکل پیدا کرده ایم.
مشکل بزرگترین مجموع اعداد
با یک مثال از جنس گراف توضیحات این الگوریتم را ادامه می دهم و در ادامه مثال از جنس دیگری هم برایتان خواهد آورد. به گراف زیر نگاه کنید:
مشکل زمان بندی
با مثالی متفاوت ادامه می دهیم، یکی از مسائل رایج، مشکل زمانبندی است. فرض کنید یک سالن جلسه داریم و زمان شروع و پایان جلسه ها، به ما داده شده است. اکنون وظیفه ی شما این است که به گونه ای این جلسه ها را برنامه ریزی کنید که بیشترین تعداد جلسه را در این سالن برگزار کنیم. و البته این جلسه ها نباید هیچ تداخلی باهم داشته باشند. یعنی زمان شروع یا پایان یک جلسه، در حین جلسه ی دیگری (یعنی بین زمان شروع و پایان آن جلسه) قرار نگیرد.
مثلا شش جلسه ی زیر را در نظر بگیرید:
A | B | C | D | E | F | |
| زمان شروع | 1 | 2 | 5 | 4 | 3 | 6 |
| زمان پایان | 6 | 3 | 9 | 6 | 5 | 10 |
اگر قرار باشد این مسئله را با الگوریتم Brute Force حل بکنیم، راه حل مان به این شکل می شود که جلسه ها را بر اساس زمان شروع شان مرتب کنیم و با اولین جلسه هم شروع کنیم. در نتیجه همه ی جلسه هایی را که با جلسه ی قبلی همپوشانی دارند را کنار بگذاریم، قطعاً به جدول درستی می رسیم، اما تعداد جلسه ها را به حداکثر نرسانده ایم. در نتیجه جواب بدست آمده بهینه نیست. اجازه دهید بعد از مرتب سازی بر اساس زمان شروع، جدول را دوباره ببینیم:
✔A | ❌B | ❌E | ❌D | ❌C | ✔F | |
| زمان شروع | 1 | 2 | 3 | 4 | 5 | 6 |
| زمان پایان | 6 | 3 | 5 | 6 | 9 | 10 |
همانطور که در جدول بالا مشاهده می کنید، با استفاده از الگوریتم Brute Force فقط دو تا از جلسات را می توانیم برگزار کنیم و 4 جلسه از دست می رود. می توان این طور در نظر گرفت که اگر جلسه ی اول را به خوبی در نظر نگیریم، برنامه ی ما شکست خورده است و عملکرد خوبی نخواهد داشت.
حالا بیایید ببینیم الگوریتم Greedy ما چه چیزی را پیشنهاد می کند. طبق الگوریتم Greedy، جلسه ها را بر اساس زمان پایانشان مرتب میکنیم، یعنی جلسه هایی را انتخاب میکنیم که زودتر تمام می شوند. جدول جلسه های جدید ما به این صورت خواهد بود:
✔B | ❌E | ❌A | ❌D | ❌C | ✔F | |
| زمان شروع | 2 | 3 | 1 | 4 | 5 | 6 |
| زمان پایان | 3 | 5 | 6 | 6 | 9 | 10 |
حالا با استفاده از الگورتیم Greedy و طبق چیزی که در جدول بالا می بینیم، جلسه های BوEوC برگزار می شود. پس در چنین مسائلی الگوریتم Greedy نتایج بهتری خواهد داشت.
در مسائلی که الگوریتمهای Greedy شکست میخورند، برنامهنویسی پویا یا Dynamic Programming که در ادامه ی همین سری مقاله ها به آن هم خواهیم رسید، ممکن است رویکرد بهتری باشد.
تمرین الگوریتم Greedy
سکان آکادمی قصد دارد به عنوان هدیه ی نوروز برای دانشجوهای برتر خود بسته ی هدیه ای را تدارک ببیند.🎁 جعبه های هدیه ای که می تواند برای دانشجوهایش بفرستد، 25 واحد ظرفیت دارند و در هر جعبه از هر کدام از موارد زیر حداکثر یک مورد می تواند قرار دهد (یعنی یا یکی از این موارد را در جعبه قرار می دهیم یا قرار نمی دهیم). در ضمن از هیچ یک این موارد نمی توان یک مقداری قرار داد. هدف اصلی ما این است که بسته هایی که برای دانشجو هایمان می فرستیم بهینه ترین هزینه را هم داشته باشد.
| هدیه | هزینه | ظرفیتی که اشغال میکند |
| Laptop | 20 | 22 |
| PlayStation | 9 | 10 |
| قلم هوشمند | 9 | 9 |
| قهوه | 6 | 7 |
کدی بنویسید که بهترین بسته ی هدیه از نظر هزینه را به ما پیشنهاد بدهد.
این مسئله، یکی از مشهورترین مسائل دنیای برنامه نویسی با عنوان Backpack Problem می باشد.
🤔 کمی درباره ی راه حل این مسئله فکر کنید، بعد دوباره برگردید و ادامه ی این مطلب را بخوانید.
دو الگوریتم Greedy وجود دارد که میتوانیم برای حل این موضوع پیشنهاد کنیم.
- در هر مرحله کالای با بیشترین قیمت را انتخاب کنیم.
- در هر مرحله کوچکترین کالا را انتخاب کنیم.
الگوریتم بیشترین قیمت: در ابتدا ما Laptop را انتخاب می کنیم که هزینه ی آن معادل 20 واحد است و 22 واحد از 25 واحد ظرفیت بسته را پر می کند. حال 3 واحد دیگر ظرفیت داریم، که هیچ کدام از موارد دیگر در جعبه جا نخواهد شد. در نتیجه با فقط توانسته ایم یک Laptop در جعبه جای بدهیم.
الگوریتم کوچکترین: در این حالت ابتدا به سراغ قهوه خواهیم رفت که 7 واحد از ظرفیت بسته ی ما را می گیرد و با توجه به ظرفیت کل بسته که 25 واحد است، همچنان 18 واحد ظرفیت داریم. دومین گزینه برایمان تابلو خواهد بود با 9 واحد ظرفیت و با قرار دادن آن در بسته، 9 واحد دیگر از ظرفیت بسته مان باقی خواهد ماند. که هیچ یک از موارد بالا با این ظرفیت و یا کمتر از این وجود ندارد. در نتیجه بسته ی هدیه ما با دو کالای قهوه و تابلو، به ارزش 5 واحد بسته خواهد شد.
الگوریتم Greedy به ما دو گزینه را معرفی می کند که یکی 22 واحد هزینه و دیگری 5 واحد هزینه دارد. البته که هیچ کدام از این گزینه بهینه نیستند. یک بار جدول را بررسی کنید، ببینید به نظر شما بهینه ترین گزینه چیست؟
