به عنوان سومین الگوریتم از مجموعه ی 6 الگوریتم جادویی دنیای برنامه نویسی، قصد دارم در مورد الگوریتم Recursive (بازگشتی)، که یکی از جالبترین و پرکاربردترین الگوریتمهای برنامه نویسی است آموزشی را ارائه بدهم. در این مقاله با الگوریتم Recursive آشنا می شوید و امیدوارم در نهایت نگاهی تازه به برنامه نویسی داشته باشید و بتوانید حرفه ای تر کد بنویسید.
تا به حال از این سری مقالات دو مقاله ی دیگر با عناوین زیر منتشر شده است:
در یک جمله می توان الگوریتم Recursive را اینگونه معرفی کرد که:
این الگوریتم، خود را به طور مکرر فراخوانی می کند تا زمانی که مشکل حل شود.
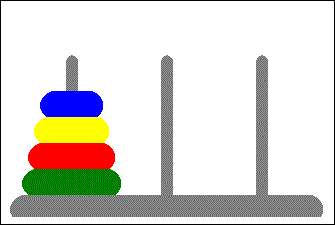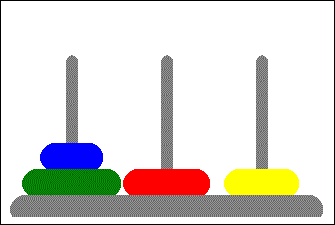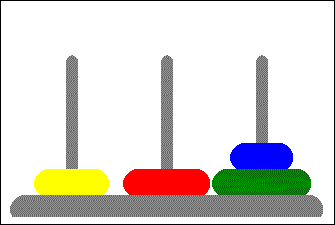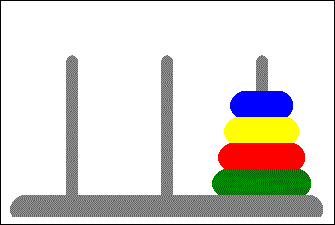
با استفاده از این الگوریتم، می توان مسائلی مانند برج هانوی (Tower of Hanoi) را به راحتی حل کرد. البته یکی از مشکلات اساسی در این الگوریتم، که باید به آن دقت شود، مدیریت حافظه است.
بازگشت (Recursion)، ابزاری است که اغلب توسط توسعه دهندگان، استفاده نمی شود زیرا تصور می کنند این الگوریتم کند است و فضا را هدر می دهد. اما چندین تکنیک وجود دارد که می توان از آنها، برای به حداقل رساندن یا حذف این مشکلات استفاده کرد.
برای دانشجویان جدید علوم کامپیوتر و برنامه نویس های تازه کار، مفهوم برنامه نویسی بازگشتی اغلب دشوار است. شاید علت اصلی آن عدم شهودی بودن آن باشد. برای همین وقتی مسئله ای را به این افراد می دهیم، خیلی کم پیش می آید که از این الگوریتم برای حل مسئله استفاده کنند.
برای افرادی که برنامه نویس تازه کار هستند، یک تعریف کمی بهتر ولی همچنان ساده از بازگشت می تواند به این صورت باشد:
بازگشت زمانی رخ می دهد که یک تابع به طور مستقیم یا غیرمستقیم خود را فراخوانی کند.
یک مثال کلاسیک از توابع بازگشتی محاسبه ی فاکتوریل یک عدد صحیح است، در زیر شبه کدی وجود دارد که با استفاده از الگوریتم بازگشتی فاکتوریل را پیدا می کند:
int factorial(int n)
{
if(n == 1)
{
return 1;
}
else
{
return n * factorial(n ‑ 1);
}
}برای کسانی که شاید با فاکتوریل آشنا نباشند توضیح می دهم که فاکتوریل (Factorial) هر عدد طبیعی در ریاضی، از حاصل ضرب آن عدد در تمام اعداد طبیعی کوچک تر از آن به جز صفر به دست میآید. فاکتوریل عددی مانند n را !n مینویسند و «اِن فاکتوریل» می خوانند. همچنین طبق قرارداد، فاکتوریل صفر همیشه برابر با یک است.
مثلا:
24 = 1*2*3*4 = !4
برای تشریح کد بالا، ابتدا یک تابع با نام ()factorial تعریف کردیم که ورودی آن یک عدد صحیح است. حالا اگر ورودی مورد نظر 1 باشد 1 را به عنوان خروجی تابع بر می گردانیم، در غیر اینصورت عدد ورودی را در حاصل فراخوانی همین تابع، با ورودی یک واحد کمتر ضرب می کنیم. و این مراحل آنقدر تکرار می شود که x-1 مساوی صفر باشد. در این صورت به عنوان آخرین عدد 1 در عدد قبلی ضرب می شود.
همانطور که می بینید، تا زمانی که عدد ورودی تابع بیشتر از صفر باشد این تابع اجرا می شود و مجددا خودش را فراخوانی می کند. نقطه ی پایان این حلقه ی تکرار را base case می نامند. هر تابع recursive ای باید حداقل یک base case (حالت پایه) داشته باشد و تضمین دهد که حتما به آن نقطه می رسیم.
هرچند که پیاده سازی این الگوریتم بسیار ساده است. ولی کاربردهای بسیار زیادی می تواند داشته باشد. البته خطرهایی هم دارد که اصلی ترین آن، گیر افتادن برنامه ی شما در حلقه ی نابود کننده ی بینهایت است که در نتیجه حافظه ی سیستم پر می شود. پس همیشه دقت داشته باشید، قبل از هر کاری حالت خروج از این حلقه ی تکرار را در کدتان تعریف کنید.اگر در تابع بالا شرط این که عدد ورودی یک بود بجای فراخوانی دوباره ی تابع، یک را برگرداند را تعریف نکرده بودیم، وارد infinite loop یا حلقه ی بینهایت می شدیم که این حلقه های بی نهایت جهنم برنامه نویسان است😉
مثال دیگری که برای استفاده از الگوریتم بازگشتی خوب است به آن اشاره کنیم؛ محاسبهی سری فیبوناچی است. برای بررسی چگونگی استفاده از این الگوریتم در محاسبهی سری فیبوناچی، به مقاله بررسی انواع روشهای محاسبه سری فیبوناچی مراجعه کنید.
مراحل اصلی برنامه های بازگشتی
هر برنامه بازگشتی، مراحلی اصلی ای را دنبال می کند که به شرح زیر است:
- الگوریتم را راه اندازی کنید. برنامه های بازگشتی اغلب برای شروع، به یک مقدار اولیه نیاز دارند. این کار یا با استفاده از پارامتری که به تابع ارسال میشود یا توسط یک تابع دیگر که غیر بازگشتی است اما مقادیر اولیه را برای محاسبه بازگشتی در اختیار تابع بازگشتی قرار می دهد، انجام میشود.
- بررسی کنید که آیا مقدار(های) فعلی که در حال پردازش آن هستید با base case (حالت پایه) مطابقت دارد یا خیر. اگر چنین است، مقدار را پردازش کرده و برگردانید.
- پاسخ را در قالب یک زیرمسئله یا مسئله ی کوچکتر یا ساده تر تعریف کنید.
- الگوریتم را روی آن مسئله ی کوچکتر یا ساده تر اجرا کنید.
- نتیجه را با همان فرمولی که در نیازمندی تابع آمده است، ترکیب کنید.
- نتیجه را برگردانید.
Linked List و توابع بازگشتی
ابتدا بیایید با ساختار داده (Data Structure) جذابی به نام Linked List آشنا بشویم. لیست پیوندی (Linked List) یک ساختار داده خطی است که در آن عناصر در مکان هایی از حافظه، که به هم پیوسته هستند ذخیره نمی شوند. عناصر موجود در یک لیست پیوندی با استفاده از نشانگرها (pointers) همانطور که در تصویر زیر نشان داده شده است پیوند داده شده اند:
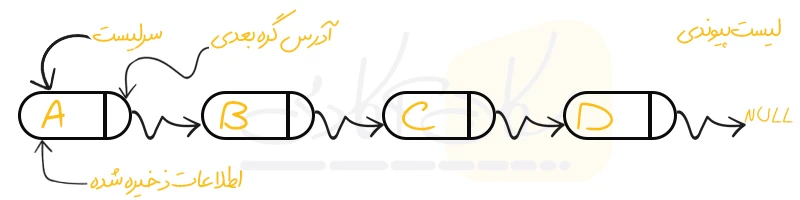
به عبارت ساده، یک لیست پیوندی شامل گره هایی است که هر گره حاوی دو فیلد است. یک فیلد داده ای را ذخیره می کند و دیگری اشاره گر به گره بعدی در لیست است. و آخرین گره هم به عنوان اشاره گر NULL را نگه می دارد که به معنای رسیدن به انتهای لیست می باشد.
مسئله ی جمع اعداد یک لیست پیوندی
حالا فرض کنید لیستی از اعداد داریم و می خواهیم حاصل جمع این اعداد را بدست بیاوریم. مراحلی که برای این کار باید طی کنیم عبارت اند از:
- راه اندازی الگوریتم؛ مقدار اولیه برای این الگوریتم، مقدار ذخیره شده در اولین گره از لیست پیوندی مان است که به این تابع داده می شود.
- مشخص کردن Base Case یا حالت پایه؛ حالت پایه زمانی اتفاق می افتد که به مقدار NULL برسیم. باید رسیدن به NULL را در تابع تشخیص دهیم و در این زمان صفر را برگردانیم.
- فراخوانی تابع با مسئله ای کوچکتر؛ در این مرحله، لازم است پاسخ مسئله را بسازیم. برای این کار باید عدد موجود در گره ای که خوانده ایم را با فراخوانی همین تابع جمع برای بقیه ی لیست، جمع کنیم.
- در آخر هم که به NULL رسیدیم فراخوانی تابع بازگشتی تمام می شود.
به شبه کد زیر دقت کنید:
int sum_list(struct list_node *l)
{
if(l == NULL)
return 0;
return l.data + sum_list(l.next);
}مسئله ی جستجوی یک کلمه در یک لیست
حالا فرض کنید قرار است در یک لیستی از کلمات، به دنبال یک کلمه ی خاص بگردید. در این حالت الگوریتم شما به راحتی می تواند اینگونه طراحی شود که: هر گره ی لیست را بخوانیم، اگر با کلمه ی مورد نظر برابر بود نتیجه را برگردانیم و در غیر اینصورت دوباره همین تابع را با گره ی بعدی لیست فراخوانی کنیم. در این مسئله Base Case شما چه چیزی است؟
اگر فکر می کنید Base Case شما باید پیدا کردن کلمه ی مورد نظر در لیست باشد، متاسفانه باید بهتون بگم که در حلقه ی بینهایت گیر افتادید. زیرا ممکن است کلمه ای که دنبال آن هستید اصلا در لیست وجود نداشته باشد. پس در این شرایط باید Base Case دیگری هم در نظر بگیریم. Base Case دوم این است که اگر به انتهای لیست رسیدیم، دیگر ادامه ندهیم.
حلقه (loop) یا تابع بازگشتی (Recursive)، مسئله این است!
عموما وقتی به یک برنامه نویس تازه کار، مسئله ای داده می شود که راه حل آن برنامه نویسی بازگشتی هست، راه حلی که به ذهن او می رسد، استفاده از حلقه به جای تابع بازگشتی است. برای همین دوست دارم در این بخش کمی حلقه و تابع بازگشتی را باهم مقایسه کنم تا متوجه شویم که آیا برنامه نویسان تازه کار حق دارند اولین چیزی که به ذهن شان می رسد، حلقه باشد یا خیر؟
تکرار
در حلقه ها: یک تکه کد به طور مکرر تکرار می شود تا نتیجه حاصل شود. با تمام شدن آن تکه کد و یا رسیدن به دستور continue حلقه دوباره تکرار می شود.
در توابع بازگشتی: یک تکه کد به طور مکرر تکرار می شود تا نتیجه حاصل شود. و زمانی دوباره کد اجرا می شود که تابع ما، دوباره خودش را فراخوانی کند.
شرط پایان
در حلقه: برای تضمین پایان یافتن حلقه، باید یک یا چند شرط وجود داشته باشد که باعث تمام کردن کار حلقه شود و باید در نقطه ای تضمین شود که حتما به یکی از این شرایط برخواهیم خورد.
در توابع بازگشتی: برای تضمین خاتمه یک تابع بازگشتی، به یک حالت پایه نیاز داریم که باعث میشود تابع دوباره تکرار نشود.
وضعیت
در حلقه: وضعیت فعلی با پیشرفت حلقه به روز می شود.
در توابع بازگشتی: وضعیت فعلی به عنوان پارامتر، ارسال می شود.
همانطور که می بینید، توابع بازگشتی و حلقه ها نقطه های اشتراک زیادی دارند. در واقع، حلقه ها و توابع بازگشتی را می توان قابل تعویض بایکدیگر در نظر گرفت. تفاوت در این است که با توابع بازگشتی، شما به ندرت مجبور به تغییر هر متغیری هستید، فقط مقادیر جدید را به عنوان پارامتر برای فراخوانی تابع بعدی ارسال می کنید. این کار به شما امکانی را می دهد که تمام مزایای نداشتن یک متغیر قابل به روز رسانی را در عین داشتن رفتار تکراری و حالت دار حفظ کنید.
هر کدام از این مزایای اشاره شده در یک برنامه ی حرفه ای، مسئله ی مهمی هستند که باید رعایت شود. به برنامه نویس های تازه کار، پیشنهاد می کنم اگر بین استفاده از تابع بازگشتی یا حلقه مردد بودند، حتما تابع بازگشتی را انتخاب کنند. زیرا هم کدشان حرفه ای تر به نظر می رسد، و هم احتمال اینکه تصمیم شان غلط باشد، خیلی کمتر است.
تمرین الگوریتم Recursive
در سایت سکان آکادمی دوره ی آموزش کاربردی داکر ارائه شده است. قصد داریم در ظاهر برنامه، به دانشجویی که در دوره ثبت نام کرده است بگوییم چند ساعت طول می کشد تا بتواند این دوره را سپری کرده و برنامه ی هایی که می نویسد را Dockerize کرده و روی کانتینرهایی بالا بیارود. لطفا کدی بنویسید که زمان تخمینی مطالعه ی هر بخش را باهم جمع کرده و برای هر بخش دو برابر زمان مطالعه، زمان تمرین درنظر بگیرید (یعنی اگر بخشی را طی 5 دقیقه می تواند بخواند، 10 دقیقه هم زمان تمرین نیاز دارد. که مجموع زمانی که برای یادگیری آن بخش لازم است 15 دقیقه خواهد بود). در نهایت زمان نهایی یادگیری را برگردانید.
برای انجام این کار، یکی از ساده ترین راه حل ها تهیه ی آرایه ای از زمان تخمینی مطالعه ی هر بخش می باشد. و نیاز است روی این آرایه یک تابع بازگشتی بنویسید.
