الگوریتم kNN یا K نزدیکترین همسایه با scikit-learn

در این مقاله نحوه و زمان استفاده از الگوریتم دسته‌بندی k-نزدیک‌ترین همسایه (kNN) با scikit-learn ، با تمرکز بر مفاهیم، گردش کار و کاربردهای آن، توضیح داده خواهد شد. همچنین در مورد معیارهای فاصله و نحوه انتخاب بهترین مقدار برای k با استفاده از اعتبارسنجی متقابل (cross validation) نیز صحبت می‌شود. برای درک کامل مفاهیم این مقاله، باید دانش اولیه از پایتون و تجربه کار با دیتافریم‌ها (DataFrames) را داشته باشید.

الگوریتم kNN یا k-nearest neighbors یک مدل یادگیری ماشین نظارت شده محبوب است که هم برای دسته‌بندی و هم برای رگرسیون استفاده می‌شود (این مقاله بر ساخت یک مدل دسته‌بندی تمرکز می کند) و یک روش مفید برای یادگیری مفاهیم توابع فاصله، سیستم های رأی‌گیری و بهینه سازی هایپر‌پارامترها است.

Evelyn Fix و Joseph Hodges این الگوریتم را در سال 1951 توسعه دادند که بعد از آن، توسط Thomas Cover گسترش یافت. الگوریتم k نزدیکترین همسایه (kNN)، اگرچه به اندازه گذشته محبوب نیست، اما به دلیل سادگی و دقت آن، هنوز یکی از الگوریتم هایی است که در علم داده به طور گسترده استفاده می‌شود. با این حال، در نظر داشته باشید که با رشد مجموعه داده، KNN به طور فزاینده‌ای ناکارآمد می‌شود و عملکرد کلی مدل را به خطر می‌اندازد. این مدل معمولاً برای سیستم‌های توصیه ساده، تشخیص الگو، داده کاوی، پیش بینی بازار مالی، تشخیص نفوذ و غیره استفاده می‌شود.

الگوریتم KNN غیرپارامتریک است، به این معنی که هیچ فرضی در مورد توزیع اساسی داده‌ها ندارد و گاهی اوقات با روش بدون نظارت خوشه‌بندی k-میانگین (k-Means Clustering) اشتباه گرفته می‌شود، اما توجه داشته باشید که خوشه‌بندی با دسته‌بندی متفاوت است. دسته‌بندی در یادگیری ماشین یک کار یادگیری نظارت شده است که شامل پیش بینی برچسب دسته یک نقطه داده به عنوان ورودی است. این الگوریتم بر روی یک مجموعه داده برچسب‌گذاری شده آموزش داده می‌شود و از ویژگی‌های ورودی برای یادگیری نگاشت بین ورودی‌ها و برچسب‌های کلاس مربوطه استفاده می‌کند. سپس، از مدل آموزش دیده، برای پیش بینی داده‌های جدید و دیده نشده استفاده می‌کند.

مروری بر الگوریتم kNN (k نزدیکترین همسایه) 

kNN یک الگوریتم ساده و شهودی است که نتایج خوبی را برای طیف گسترده‌ای از مسائل دسته‌بندی ارائه می‌دهد. پیاده سازی و درک آن آسان است و برای مجموعه داده های کوچک و بزرگ کاربرد دارد. با این حال، با برخی از اشکالات نیز همراه است و نقطه ضعف اصلی آن، این است که می تواند از نظر محاسباتی برای مجموعه داده‌های بزرگ یا فضاهای ویژگی با ابعاد بالا، گران و پرهزینه باشد.

همانطور که گفته شد، الگوریتم kNN را می‌توان برای مسائل رگرسیون یا دسته‌بندی استفاده کرد. مسائل رگرسیون از مفهومی مشابه با مسائل دسته‌بندی استفاده می‌کنند، با این تفاوت که، میانگین k نزدیک‌ترین همسایه‌ را برای پیش‌بینی در نظر می‌گیرند. در واقع، تمایز اصلی این دو روش، این است که دسته‌بندی برای مقادیر گسسته استفاده می‌شود، در حالی که رگرسیون برای مقادیر پیوسته استفاده می‌شود. قبل از انجام دسته‌بندی، نحوه محاسبه فاصله باید تعریف شود. در بیشتر موارد، فاصله اقلیدسی مورد استفاده قرار می‌گیرد که در ادامه متن به آن پرداخته می‌شود.

همچنین شایان ذکر است که الگوریتم kNN بخشی از خانواده مدل‌های «یادگیری تنبل» (lazy learning) است. در یادگیری ماشینی سنتی، الگوریتم‌ها داده‌ها را جمع‌آوری می‌کنند، بر روی آن آموزش می‌دهند و یک مدل آموزش‌دیده تولید می‌کنند که قادر به پیش‌بینی مجموعه داده‌های دیده نشده با سطح مشخصی از دقت است. با این حال، الگوریتم های یادگیری تنبل یک رویکرد متمایز را استفاده می کنند.

الگوریتم‌های یادگیری تنبل همان مکانیزم زیربنایی الگوریتم‌های سنتی را حفظ می‌کنند، اما نحوه مدیریت داده‌ها را تغییر می‌دهند. در طول مرحله آموزش یادگیری تنبل، الگوریتم داده‌ها را به عنوان ورودی می‌پذیرد اما از آموزش فعال بر روی آن خودداری می‌کند. در عوض، داده‌ها را برای استفاده بعدی ذخیره می‌کند و آموزش مدل واقعی در مرحله پیش بینی رخ می‌دهد. از آنجایی که این روش، برای ذخیره تمام داده‌های آموزشی خود به شدت به حافظه متکی است، به آن روش یادگیری مبتنی بر نمونه ( instance-based learning) یا مبتنی بر حافظه (memory-based learning) نیز گفته می‌شود.

در مقابل یادگیری تنبل، یادگیری مشتاق (Eager learning) وجود دارد که نوعی از یادگیری ماشینی است که در آن سیستم یک مدل تعمیم یافته را در طول مرحله آموزش، قبل از انجام هرگونه پرس و جو می‌سازد.

الگوریتم kNN چگونه کار می‌کند؟

الگوریتم k-Nearest Neighbors (kNN) مانند یک سیستم رأی گیری عمل می کند. این الگوریتم برای دسته‌بندی یک نقطه داده جدید، به «k» نزدیک‌ترین نقاط اطراف آن در مجموعه داده نگاه می‌کند (که در آن «k» عددی است که شما انتخاب می‌کنید) و دسته‌ای را برای نقطه داده جدید انتخاب می‌کند که بیشترین نقاط همسایه آن، آن دسته را دارند. انتخاب مقدار "k" مهم است زیرا می تواند بر میزان دقت الگوریتم تأثیر بگذارد.

اگرچه در اغلب مقالات، از اصطلاح «رای اکثریت»، برای بررسی همسایگی استفاده می‌شود، اما اصطلاح درست «رای اکثریت نسبی» است. "رای اکثریت" به این معنی است که بیش از 50 درصد از همسایگان با شما موافق هستند، که این فقط زمانی که دو گروه وجود داشته باشد، به خوبی کار می کند. اما اگر بیش از دو گروه وجود داشته باشد، چگونه باید تصمیم بگیریم؟ در این مواقع، با کمتر از 50 درصد آرا می توان تصمیم گرفت. به عنوان مثال، اگر یک گروه بیش از 25 درصد آرا را به دست آورد، برچسب آن گروه، برنده است.

برای روشن شدن این موضوع، تصور کنید در یک روستای کوچک زندگی می کنید و می خواهید تصمیم بگیرید که از کدام حزب سیاسی حمایت کنید. برای کمک به تصمیم گیری، از نزدیک ترین همسایگان خود می‌پرسید که چه فکر می کنند و به کدام حزب رای می‌دهند. اگر اکثر آنها بگویند که از حزب الف حمایت می کنند، شما نیز احتمالاً از حزب الف حمایت خواهید کرد. الگوریتم kNN کاری مشابه انجام می دهد - یک نقطه داده جدید را بر اساس نزدیک ترین همسایگان آن طبقه بندی می کند.

حالا یک مثال دیگر را در نظر بگیرید. فرض کنید شما اطلاعاتی مانند قطر و اندازه میوه ها، برای مثال، انگور و گلابی دارید، و این اطلاعات را روی یک نمودار رسم کرده‌اید. حالا، وقتی میوه جدیدی به دست می آورید، آن را روی همان نمودار رسم می کنید و به k نزدیک ترین نقطه اطراف آن نگاه می کنید. اگر  k را برابر سه انتخاب کنید، باید به سه نقطه نزدیک نگاه کنید. اگر همه گلابی باشند، می توانید مطمئن باشید (100%) که میوه جدید گلابی است. اما اگر چهار نقطه نزدیک را انتخاب کنید (۴k=)، متوجه می‌شوید که سه نقطه گلابی و یکی انگور است، که این بار بر اساس رای همسایگانش، می‌توانید با 75 درصد اطمینان بگویید که میوه جدید گلابی است.

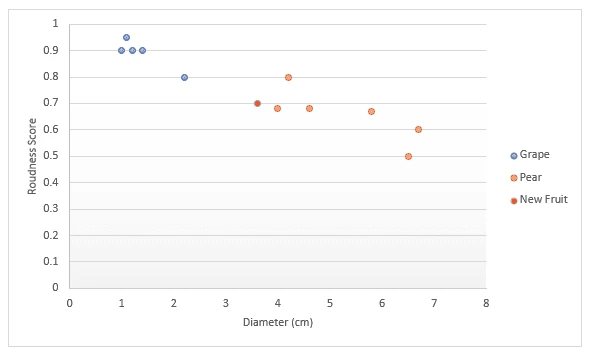
بنابراین، می‌توانیم الگوریتم kNN را به چند بخش تقسیم کنیم: 

ابتدا باید فاصله بین نقاط داده جدید و سایر نقاط داده در مجموعه آموزشی را محاسبه کنیم و نزدیک‌ترین k نقطه را انتخاب کنیم. متریک مورد استفاده برای محاسبه فاصله می‌تواند بسته به مسئله متفاوت باشد. متریک فاصله اقلیدسی معمولا بیشترین استفاده را دارد. پس از شناسایی k نزدیکترین همسایه، الگوریتم برچسب کلاس اکثریت را در میان آن همسایگان، به نقطه داده جدید اختصاص می‌دهد. همانطور که در تصویر زیر می‌بینید، اگر دو برچسب "آبی" و یک برچسب "قرمز" باشد، الگوریتم برچسب "آبی" را به یک نقطه داده جدید اختصاص می‌دهد.

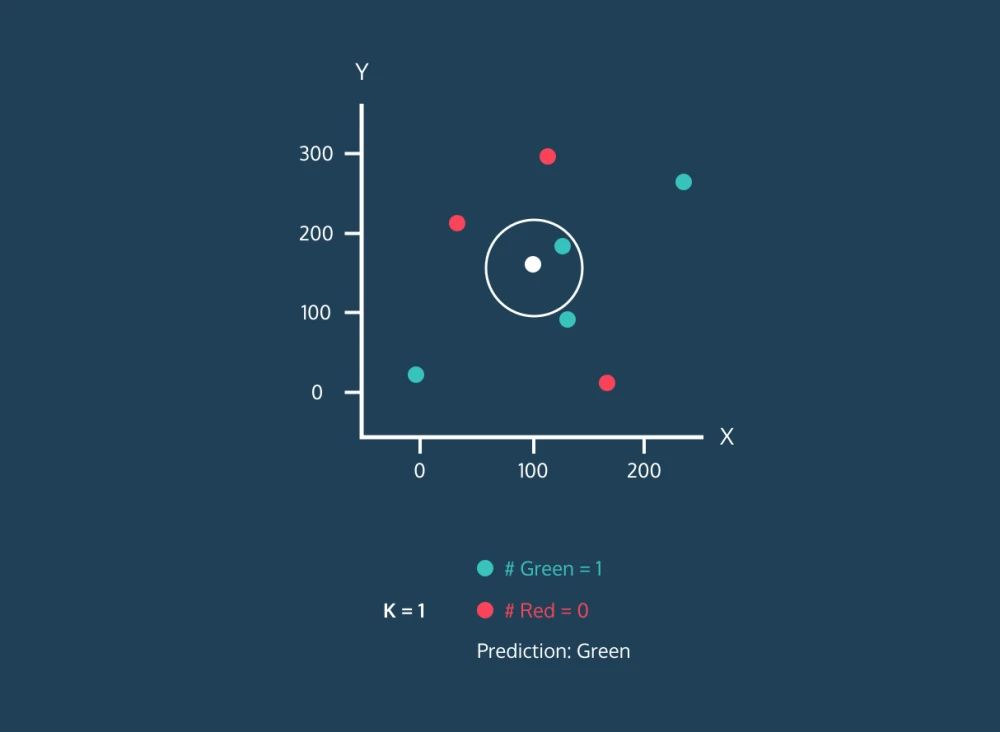
به طور خلاصه، می‌توان الگوریتم kNN را به صورت زیر بیان کرد:

1. مقدار k را انتخاب کنید که تعداد نزدیکترین همسایه هایی است که برای پیش بینی استفاده می‌شود.
2. فاصله بین آن نقطه و تمام نقاط مجموعه آموزشی را محاسبه کنید.
3. k  نزدیکترین همسایه را بر اساس فواصل محاسبه شده انتخاب کنید.
4. برچسب کلاس اکثریت را به نقطه داده جدید اختصاص دهید.
5. مراحل 2 تا 4 را برای تمام نقاط داده در مجموعه آزمایشی تکرار کنید.
6. دقت الگوریتم را ارزیابی کنید.

توجه کنید که مقدار "k" توسط کاربر ارائه می‌شود و می‌توان از آن برای بهینه سازی عملکرد الگوریتم استفاده کرد. مقادیر k کوچکتر می‌تواند منجر به بیش از حد برازش شوند و مقادیر بزرگتر می تواند منجر به عدم تناسب و کم برازشی شوند. بنابراین، یافتن مقادیر بهینه‌ای که ثبات و بهترین تناسب را فراهم می کند، بسیار مهم است. در ادامه این مقاله نحوه یافتن بهترین مقدار برای k و روش‌های مختلف اندازه‌گیری فاصله را توضیح خواهیم داد.

مجموعه داده

برای درک کامل الگوریتم  kNN، اجازه دهید با یک مطالعه موردی (case study) کار کنیم که ممکن است در حین کار به عنوان دانشمند داده به آن برخورد کنید. بیایید فرض کنیم شما یک دانشمند داده در یک فروشگاه آنلاین هستید و وظیفه شناسایی تراکنش‌های تقلبی را بر عهده دارید. تنها ویژگی‌هایی که در این مرحله دارید عبارتند از:

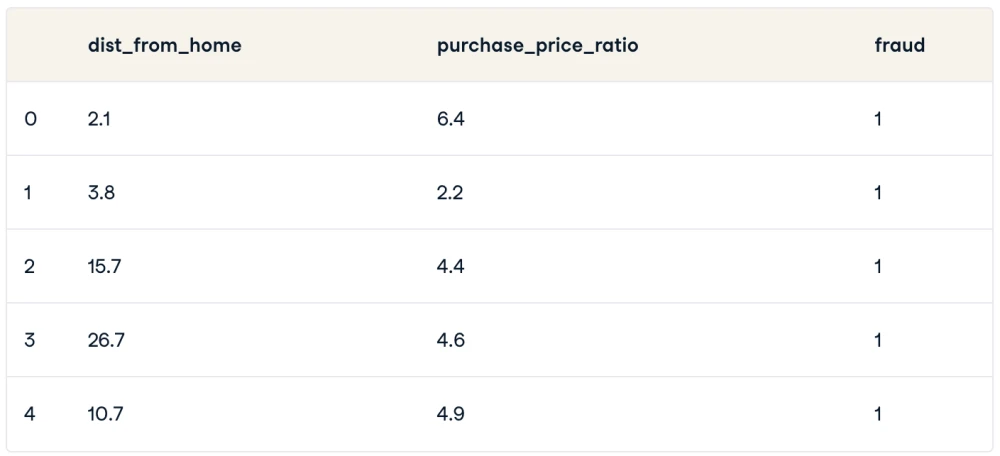
• dist_from_home : فاصله بین خانه کاربر و محل انجام تراکنش.
• purchase_price_ratio: نسبت قیمت کالای خریداری شده در تراکنش به میانه قیمت خرید آن توسط کاربر.

مجموعه داده  39 مشاهده دارد که همان تراکنش های فردی هستند و متغیر df که به مجموعه داده اشاره می‌کند، به شکل زیر است:

گردش کار k نزدیکترین همسایه

ما در این‌جا، برای fit و آموزش (train) مدل، اینفوگرافیک گردش کار یادگیری ماشین را دنبال خواهیم کرد.

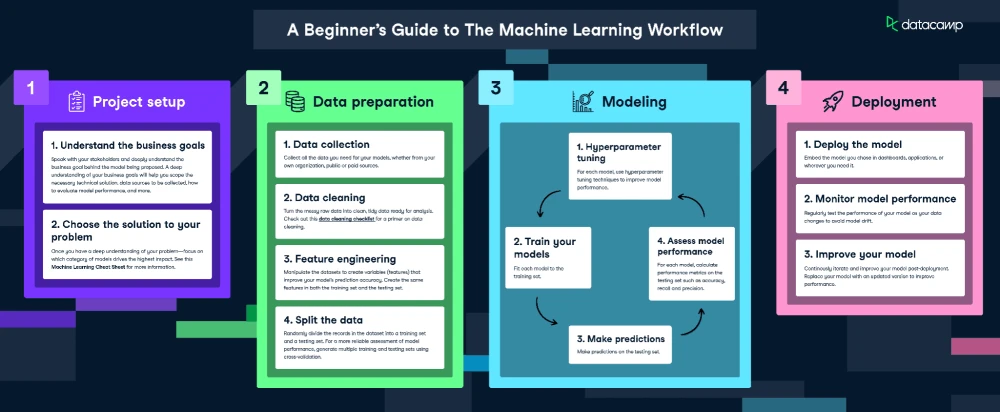
البته از آنجایی که داده‌های ما کاملاً تمیز هستند، ما همه مرحله را نیاز نیست انجام دهیم و فقط موارد زیر را انجام خواهیم داد:

• مهندسی ویژگی
• تقسیم داده ها
• آموزش مدل 
• تنظیم فراپارامتر
• ارزیابی عملکرد مدل

تصویرسازی داده‌ها 

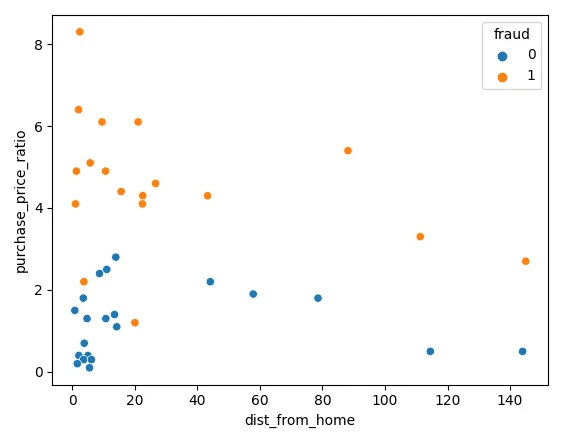
بیایید با تصویرسازی داده‌های خود با استفاده از Matplotlib شروع کنیم. می‌توانیم دو ویژگی خود را در یک نمودار پراکندگی رسم کنیم.

sns.scatterplot(x=df['dist_from_home'],y=df['purchase_price_ratio'], hue=df['fraud'])

همانطور که می‌بینید، تفاوت آشکاری بین این تراکنش‌ها وجود دارد، به طوری که تراکنش های تقلبی در مقایسه با میانه سفارش مشتریان، مقدار بسیار بیشتری دارند. تفسیر روندهای مربوط به فاصله از خانه تا حدودی دشوار است، زیرا تراکنش‌های غیرتقلبی معمولاً به خانه نزدیک‌تر هستند (البته دارای چندین نقطه پرت نیز هستند).

نرمال سازی و تقسیم داده‌ها

هنگام آموزش هر مدل یادگیری ماشین، مهم است که داده‌ها را به داده‌های آموزشی و آزمایشی تقسیم کنید. داده‌های آموزشی برای برازش (fit) مدل استفاده می‌شوند. الگوریتم مدل از داده‌های آموزشی برای یادگیری رابطه بین ویژگی ها و هدف استفاده می‌کند و سعی می کند الگویی را در داده های آموزشی پیدا کند که بتواند از آن برای پیش بینی داده های جدید و نادیده استفاده کند. داده‌های آزمایشی برای ارزیابی عملکرد مدل استفاده می شوند. در واقع، مدل از داده‌های آزمایشی استفاده می‌کند تا مقادیر هدف آن ها را پیش‌بینی کند و با مقایسه این پیش‌بینی‌ها با مقادیر هدف واقعی، عملکرد مدل را مشخص کند.

هنگام آموزش یک دسته‌بندی کننده kNN، نرمال سازی ویژگی ها ضروری است. این به این دلیل است که kNN فاصله بین نقاط را اندازه گیری می‌کند. پیش فرض استفاده از فاصله اقلیدسی است که جذر مجموع مربعات اختلاف فاصله بین دو نقطه است. در مثال ما، purchase_price_ratio بین 0 تا 8 است در حالی که  dist_from_home  بسیار بزرگتر است. اگر این را فاصله‌ها را نرمال نکنیم، محاسبه ما به شدت با dist_from_home  بایاس می‌شود، زیرا اعداد آن بزرگتر هستند.

توجه کنید که ما باید داده ها را “پس” از تقسیم به مجموعه های آموزشی و آزمایشی نرمال سازی کنیم. این برای جلوگیری از "نشت داده" (data leakage) است زیرا اگر ما همه داده ها را به طور همزمان نرمال سازی کنیم، نرمال سازی اطلاعات بیشتری در مورد مجموعه تست به مدل می دهد.

کد زیر داده‌ها را به دو بخش آموزشی/آزمایشی تقسیم می کند، سپس با استفاده از مقیاس کننده استاندارد scikit-learn (scikit-learn’s standard scaler) آن‌ها را نرمال می‌کند. بنابراین، ما باید ابتدا ()fit_transform را روی داده‌های آموزشی فراخوانی کنیم که مقیاس کننده ما را با میانگین و انحراف استاندارد داده های آموزشی fit می‌کند. سپس می‌توانیم با فراخوانی ()transform که از مقادیر آموزش داده شده قبلی استفاده می‌کند، این را به داده‌های آزمایشی اعمال کنیم.

# Split the data into features (X) and target (y)
X = df.drop('fraud', axis=1)
y = df['fraud']
# Split the data into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# Scale the features using StandardScaler
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

برازش و ارزیابی مدل

ما اکنون آماده آموزش مدل هستیم. برای این کار، از مقدار ثابت 3 برای k استفاده می کنیم، اما باید بعداً این مقدار را بهینه کنیم. ما ابتدا نمونه‌ای از مدل kNN ایجاد می‌کنیم، سپس آن را با داده‌های آموزشی خود fit می‌کنیم. ما هم ویژگی ها و هم متغیر هدف را به آن ارسال می کنیم تا مدل بتواند یاد بگیرد.

knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)

حال که مدل آموزش دیده آماده است، می‌توانیم پیش‌بینی‌هایی را روی مجموعه داده آزمایشی انجام دهیم، که بعداً می‌توانیم از آن برای محاسبه عملکرد مدل استفاده کنیم.

y_pred = knn.predict(X_test)

ساده ترین راه برای ارزیابی این مدل استفاده از دقت (accuracy) است. ما پیش‌بینی‌ها را در برابر مقادیر واقعی در مجموعه تست بررسی می‌کنیم و تعداد پیش‌بینی های درست مدل‌ها را می‌شماریم.

accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
Accuracy: 0.875

همانطور که می‌بینید امتیاز (score) به دست آمده، نسبتا خوب است! با این حال، ممکن است بتوانیم با بهینه‌سازی مقدار k بهتر عمل کنیم.

استفاده از اعتبارسنجی متقابل برای پیداکردن بهترین مقدار k

مقدار k در الگوریتم kNN تعیین می‌کند که چند همسایه برای تعیین دسته‌بندی یک نقطه داده جدید بررسی شود. به عنوان مثال، اگر k=1 باشد، برچسب نمونه داده جدید مشابه با کلاس نزدیکترین همسایه اش اختصاص داده می‌شود. تعریف k می‌تواند یک عمل متعادل کننده باشد زیرا مقادیر مختلف می تواند منجر به بیش از حد برازش یا کم برازشی شود. مقادیر کمتر k می تواند باعث واریانس بالا اما بایاس کم شوند و مقادیر بزرگتر k ممکن است منجر به بایاس زیاد و واریانس کمتر شوند. انتخاب k تا حد زیادی به داده‌های ورودی بستگی دارد زیرا داده‌هایی با مقادیر پرت یا نویز بیشتر احتمالاً با مقادیر بالاتر k عملکرد بهتری خواهند داشت. به طور کلی، توصیه می‌شود یک عدد فرد برای k در نظر بگیرید تا از گره ها (ties) در دسته‌بندی جلوگیری کنید.

متأسفانه، هیچ راه جادویی برای یافتن بهترین مقدار برای k وجود ندارد و ما باید بهترین مقدار را از طریق تست مقادیر مختلف بدست آوریم. تکنیک‌های اعتبارسنجی متقابل می‌تواند به شما در انتخاب k بهینه برای مجموعه داده‌تان کمک کند.

در کد زیر، محدوده‌ای از مقادیر را برای k انتخاب می‌کنیم و یک لیست خالی برای ذخیره نتایج خود ایجاد می‌کنیم. ما از اعتبارسنجی متقابل برای یافتن امتیازات دقت استفاده می‌کنیم، به این معنی که نیازی به ایجاد یک تقسیم آموزشی و آزمایشی نداریم، اما باید داده‌های خود را مقیاس بندی کنیم. سپس روی مقادیر حلقه زده و امتیازها را به لیست خود اضافه می کنیم.

برای اجرای اعتبارسنجی متقابل، از cross_val_score scikit-learn استفاده می‌کنیم و یک نمونه از مدل kNN را به همراه داده‌ها و تعداد تقسیم‌بندی به آن، ارسال می‌کنیم. در کد زیر، ما از پنج تقسیم استفاده کردیم که به این معنی است که مدل داده‌ها را به پنج گروه با اندازه مساوی تقسیم می‌کند و از 4 برای آموزش و 1 برای آزمایش نتیجه استفاده می‌کند. در هر گروه حلقه می‌زند و یک امتیاز دقت را محاسبه می‌کند و برای یافتن بهترین مدل، میانگین آنها را می‌گیرد.

k_values = [i for i in range (1,31)]
scores = []
scaler = StandardScaler()
X = scaler.fit_transform(X)
for k in k_values:
   knn = KNeighborsClassifier(n_neighbors=k)
   score = cross_val_score(knn, X, y, cv=5)
   scores.append(np.mean(score))

می توانیم نتایج را با کد زیر رسم کنیم:

sns.lineplot(x = k_values, y = scores, marker = 'o')
plt.xlabel("K Values")
plt.ylabel("Accuracy Score")

می توانیم از نمودار ببینیم که k = 9، 10، 11، 12، و 13 همگی دارای امتیاز دقت (accuracy score) کمی کمتر از 95٪ هستند. از آنجایی که این مقادیر k، تقریبا دارای امتیازهای برابر هستند، توصیه می شود از مقدار کمتر k استفاده کنید و این به این دلیل است که هنگام استفاده از مقادیر بالاتر k، مدل از نقاط داده بیشتری که دورتر از نقاط اصلی هستند، استفاده می کند. برای پیدا کردن نتیجه بهتر، ما می‌توانیم  از سایر معیارهای ارزیابی نیز استفاده کنیم.

معیارهای ارزیابی بیشتر

اکنون می‌توانیم مدل خود را با استفاده از بهترین مقدار k با استفاده از کد زیر آموزش دهیم:

best_index = np.argmax(scores)
best_k = k_values[best_index]
knn = KNeighborsClassifier(n_neighbors=best_k)
knn.fit(X_train, y_train)

سپس با accuracy، precision و recall ارزیابی کنیم (توجه داشته باشید که نتایج شما ممکن است به دلیل تصادفی سازی متفاوت باشد)

y_pred = knn.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
print("Accuracy:", accuracy)
print("Precision:", precision)
print("Recall:", recall)
Accuracy: 0.875
Precision: 0.75
Recall: 1.0

معیارهای فاصله (distance metrics)

به طور خلاصه، هدف از الگوریتم-k نزدیکترین همسایه، شناسایی نزدیکترین همسایگان یک نقطه داده جدید است، به طوری که بتوانیم یک برچسب کلاس به آن نقطه اختصاص دهیم. برای تعیین اینکه کدام نقاط داده به یک نقطه داده جدید و دیده‌نشده، نزدیکتر هستند، فاصله بین نقطه جدید و سایر نقاط داده باید محاسبه شود. این معیارهای فاصله به شکل گیری مرزهای تصمیم کمک می کنند و نقاط جدید را به مناطق مختلف تقسیم می‌کنند. معمولاً مرزهای تصمیم با نمودارهای Voronoi نمایش داده می‌شوند.
چندین معیار برای محاسبه فاصله وجود دارد که در این مقاله کاربردی‌ترین موارد بیان می‌شوند:

• فاصله اقلیدسی (Euclidean distance): این روش، رایج ترین معیار اندازه‌گیری فاصله است و چیزی نیست جز فاصله دکارتی بین دو نقطه در صفحه / ابرصفحه. همچنین فاصله اقلیدسی را می‌توان به عنوان طول خط مستقیمی که دو نقطه را به هم متصل می‌کند، درنظر گرفت.

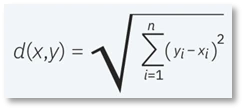
• فاصله منهتن (Manhattan distance): این روش، نیز یکی دیگر از معیارهای محبوب فاصله است که قدر مطلق بین دو نقطه را اندازه گیری می‌کند. این روش، همچنین به عنوان فاصله تاکسی (taxicab) یا فاصله بلوک شهر (city block) شناخته می‌شود زیرا معمولاً با یک grid تجسم می شود و نشان می‌دهد که چگونه می توان از یک آدرس به آدرس دیگر از طریق خیابان های شهر حرکت کرد.

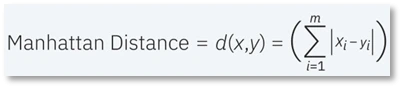
• فاصله مینکوفسکی (Minkowski distance): این معیار اندازه‌گیری فاصله، شکل تعمیم یافته معیارهای فاصله اقلیدسی و منهتن است. در فرمول زیر، می‌توانیم بگوییم که وقتی p = 2 است، همان فرمول فاصله اقلیدسی است و وقتی p = 1 است، فرمول فاصله منهتن است.

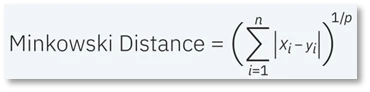
• فاصله همینگ: این تکنیک معمولاً برای بردارهای بولی یا رشته ای استفاده می شود و نقاطی را که در آن، بردارها مطابقت ندارند مشخص می کند. در نتیجه از آن به عنوان متریک همپوشانی نیز یاد می‌شود.

به عنوان مثال، اگر رشته‌های زیر را داشته باشید، فاصله همینگ 2 خواهد بود، زیرا تنها دو عدد از مقادیر متفاوت هستند.

کاربردهای kNN در یادگیری ماشین

الگوریتم kNN در کاربردهای مختلف، که عمدتاً دسته‌بندی هستند، استفاده می‌شود. برخی از این موارد استفاده عبارتند از:

1. پیش پردازش داده‌ها (Data Preprocessing): هنگام برخورد با هر مسئله یادگیری ماشین، ما ابتدا EDA را انجام می دهیم و اگر در آن متوجه شدیم که داده ها حاوی مقادیر گم شده هستند، می‌توانیم از روش‌های انتساب استفاده کنیم. یکی از این روش‌های انتساب، kNN Imputer است که یکی از روش‌های بسیار مؤثر است و عموماً به عنوان یک روش‌ پیچیده انتسابی استفاده می‌شود.
2. موتورهای توصیه (Recommendation Engines): وظیفه اصلی یک الگوریتم kNN ، اختصاص یک نقطه داده جدید به یک دسته از پیش موجود است (این دسته‌ها با استفاده از مجموعه عظیمی از مجموعه داده‌ها ایجاد شده‌اند). این دقیقاً همان چیزی است که در سیستم‌های توصیه‌گر برای اختصاص دادن هر کاربر به یک گروه خاص و سپس ارائه توصیه‌هایی به کاربر بر اساس ترجیحات آن گروه، استفاده می‌شود.
3. مالی (Finance): kNN همچنین در انواع موارد مالی و اقتصادی استفاده شده است. برای مثال، استفاده از kNN بر روی داده‌های اعتباری می‌تواند به بانک‌ها در ارزیابی ریسک وام به یک سازمان یا فرد کمک کند و برای تعیین اعتبار متقاضی وام استفاده شود.
4. مراقبت های بهداشتی (Healthcare): kNN در صنعت مراقبت های بهداشتی نیز کاربرد داشته است و خطر حملات قلبی و سرطان پروستات را پیش بینی کرده است.
5. تشخیص الگو (Pattern Recognition): kNN  همچنین در شناسایی الگوها، مانند دسته‌بندی متن و رقم کمک کرده است. این الگوریتم به ویژه در شناسایی شماره های دست نویسی که در فرم‌ها یا پاکت های پستی وجود دارند، بسیار مفید بوده است. اگر الگوریتم kNN را با استفاده از مجموعه داده MNIST آموزش و سپس فرآیند ارزیابی را انجام دهید، با این واقعیت مواجه می‌شوید که الگوریتم‌های kNN  بسیار خوب و با دقت بسیار بالا عمل می‌کنند.

مزایا و معایب الگوریتم kNN

درست مانند هر الگوریتم یادگیری ماشینی، kNN  نقاط قوت و ضعف خود را دارد و بر اساس پروژه و برنامه شما، ممکن است انتخاب مناسبی باشد یا نباشد. 

مزایا:

1. یادگیری و پیاده سازی آسان: با توجه به سادگی و دقت الگوریتم، یکی از اولین دسته‌بندی کننده هایی است که یک دانشمند داده جدید یاد می گیرد.
2. به راحتی fit می‌شود: با اضافه شدن نمونه های آموزشی جدید، الگوریتم می‌تواند به سادگی برای محاسبه هر داده جدید تنظیم شود زیرا تمام داده های آموزشی در حافظه ذخیره می شود. همانطور که گفته شد، kNN  مدل نمی سازد، داده های آموزشی را ذخیره می کند و از آن برای پیش بینی استفاده می کند.
3. همه کاره است: این الگوریتم می تواند هم برای کارهای رگرسیون و هم برای دسته‌بندی استفاده شود. همچنین، این الگوریتم در مورد توزیع داده ها مفروضاتی ایجاد نمی کند که آن را برای طیف وسیعی از مسائل مناسب می کند
4. نتایج قابل تفسیر: این الگوریتم نتایج قابل تفسیری را ارائه می دهد که می تواند تصویرسازی و درک شود زیرا کلاس پیش‌بینی شده بر اساس برچسب های نزدیکترین همسایگان در داده‌های آموزشی است.
5. بررسی روابط غیرخطی: kNN در مورد مرز تصمیم گیری بین کلاس ها مفروضاتی ایجاد نمی کند و این ویژگی به آن اجازه می دهد تا روابط غیرخطی بین ویژگی ها را بتواند بررسی کند.
6. تعداد کم فراپارامتر: kNN فقط به یک مقدار k و یک متریک فاصله نیاز دارد که در مقایسه با سایر الگوریتم‌های یادگیری ماشین پایین است.

معایب

1. پر هزینه از نظر محاسباتی و حافظه: از آنجایی که kNN یک الگوریتم تنبل است، در مقایسه با سایر دسته‌بندی کننده ها، حافظه بیشتری را برای ذخیره داده‌ها اشغال می کند. این می تواند از نظر زمانی و مالی برای مجموعه داده های بزرگ و پیچیده پرهزینه باشد. همچنین، یافتن تعداد بهینه همسایگان k نیز می تواند زمان بر باشد.
2. عملکرد نامناسب برای داده‌های نویزی و نامتوازن: عملکرد  kNN برای داده های نامتعادل خوب نیست و نسبت به طبقه اکثریت بایاس نشان می‌دهد که این می تواند منجر به عملکرد ضعیف برای دسته‌های اقلیت شود. همچنین، برای داده های نویزی مناسب نیست زیرا نزدیکترین همسایه یک نقطه داده ممکن است نماینده برچسب کلاس واقعی نباشند.
3. مشکل ابعاد بالا(curse of dimensionality): الگوریتم kNN برای داده‌های ورودی با ابعاد بالا عملکرد خوبی ندارد زیرا ابعاد بالا می تواند باعث شود فاصله بین تمام نقاط داده مشابه شوند.گاهی اوقات به این پدیده پیکینگ (peaking) نیز گفته می‌شود، که در آن پس از دستیابی الگوریتم به تعداد بهینه ویژگی‌ها، ویژگی‌های اضافی میزان خطاهای دسته‌بندی را افزایش می‌دهند، به خصوص زمانی که حجم نمونه کوچک‌تر باشد.
4. مستعد بیش از حد برازش: به دلیل مشکل ابعاد بالا، kNN نیز مستعد بیش از حد برازش است. اگرچه تکنیک‌های انتخاب ویژگی و کاهش ابعاد برای جلوگیری از این اتفاق استفاده می‌شوند، اما مقدار k نیز می‌تواند بر رفتار مدل تأثیر بگذارد. مقادیر پایین‌تر k می‌توانند باعث بیش از حد برازش به داده‌ها شوند، در حالی که مقادیر بالاتر k تمایل دارند مقادیر پیش‌بینی را «هموار» کنند، زیرا میانگین‌گیری مقادیر در یک منطقه بزرگ‌تر انجام می‌دهند. با این حال، اگر مقدار k بیش از حد بزرگ باشد، می تواند باعث کم برازش شود.