اگر در حال مطالعه آمار هستید، احتمالا با دو عبارت آزمون پارامتریک و غیرپارامتریک (parametric and non-parametric test) مواجه شده‌اید. آشنایی با این اصطلاحات، برای هر کسی که به دنبال آمار و علم داده است ضروری است.

آزمون‌های پارامتریک و غیرپارامتریک (ناپارامتریک) دو روش اصلی طبقه بندی آزمون‌های آماری هستند. جنبه هیجان انگیز و پیچیده این طبقه‌بندی، به ویژه در مورد آزمون‌های غیرپارامتریک در آمار، این است که هیچ تعریف قطعی از آزمون غیرپارامتریک، وجود ندارد. این باعث می شود که درک تفاوت بین این دو اصطلاح، پیچیده تر شود و به رویکرد ظریف‌تری نیاز شود.

یکی از راه‌های متداول این است که نمونه‌هایی از آزمون‌های پارامتریک را در نظر بگیرید و سپس در مورد همتایان غیر پارامتریک آنها بحث کنید. این یکی از بهترین روش‌ها برای درک تفاوت‌ها است. در این مقاله، ما این رویکرد را برای درک این موضوع در نظر خواهیم گرفت.

مروری بر مفاهیم بنیادی آماری

قبل از ارائه تعاریف آزمون های پارامتریک و غیرپارامتریک، بررسی برخی مفاهیم مهم آماری که مبنای این آزمون‌ها هستند، حائز اهمیت است.

جمعیت

جمعیت به همه افراد یا موضوعاتی که می خواهید در مورد آن مطالعه کنید، اشاره دارد. در آمار معمولا شما هرگز نمی توانید اطلاعات مربوط به جمعیت را به طور کامل جمع آوری کنید، زیرا جمعیت بسیار بزرگ است و نمی‌توان به کل جمعیت دسترسی داشت. به عنوان مثال، فرض کنید می خواهید از درآمد همه‌ی هندی‌های شاغل مطلع شوید. در این صورت پرسش از درآمد میلیون‌ها نفر تقریباً غیرممکن است. همچنین، حجم و سرعت پردازش داده‌های جمعیت بسیار دشوار است (ممکن است باعث مشکلات سخت افزاری (حافظه محدود) شود). به عنوان مثال، اگر می‌خواهید الگوی مخارج مشتریان بانک را تحلیل کنید، تعداد تراکنش‌هایی که در هر لحظه انجام می‌شود، می‌تواند به میلیون‌ها تراکنش برسد و تجزیه و تحلیل داده های یک ماه می تواند از نظر محاسباتی آنقدر گران باشد که تحلیل را غیرممکن ‌کند.

پارامتر

برای پاسخ به هر سوال مرتبط با جمعیت، محاسباتی برای کمی کردن باید انجام شود، مانند میانگین، انحراف معیار، میانه، حداقل، حداکثر، محدوده بین چارکی، و غیره. این مقادیر معنی‌دار که جمعیت را توصیف می کنند به عنوان "پارامتر" شناخته می‌شوند.

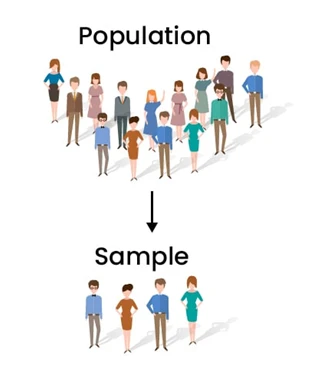
نمونه

همانطور که قبلا ذکر شد، به دلیل مسائل مختلف، داشتن اطلاعات کامل از جمعیت مورد نظر دشوار است. با این حال، برای پاسخ به بسیاری از سوالات، باید جمعیت را درک کنید. اینجاست که استفاده از نمونه ها مفید واقع می شود. نمونه‌ها چیزی نیستند جز زیرمجموعه ای از جامعه که به دلیل مفهومی معروف به قضیه حد مرکزی، جامعه را نشان می‌دهند.

قضیه حد مرکزی

قضیه حد مرکزی (CLT) بیان می کند که اگر تعداد نمونه‌ها به اندازه کافی زیاد باشد، یعنی حجم نمونه بزرگ باشد (از لحاظ نظری، بیش از 30)، میانگین همه این نمونه‌ها با میانگین جامعه یکسان خواهد بود. جنبه دیگر این قضیه این است که توزیع نمونه نرمال (گاوسی) خواهد بود حتی اگر توزیع جامعه نرمال نباشد.

توزیع

توزیع تابعی است که تمام مقادیر ممکن یک مجموعه داده نشان می‌دهد. توزیع اغلب با استفاده از نمودارهایی مانند هیستوگرام یا نمودار خطی نشان داده می شود. توزیع های مختلف دارای اشکال و ویژگی های خاص هستند که به محاسبه احتمالات کمک می کنند. این احتمالات معمولاً مربوط به احتمال وقوع یک مقدار در داده‌ها هستند که می‌توان آن را برای ایجاد فرض بزرگ‌تری در مورد فضای نمونه و جمعیتی که از آن استخراج شده است، برون یابی کرد.

انواع توزیع

توزیع می تواند متقارن یا نامتقارن باشد. توزیع‌های متقارن، توزیعی‌هایی هستند که سطح زیر منحنی سمت چپ نقطه مرکزی با سمت راست یکسان باشد. توزیع های نامتقارن کج هستند که می‌توانند مثبت یا منفی باشند. راه دیگر برای درک توزیع متقارن از نظر شکل این است که هیچ چولگی وجود نداشته باشد زیرا سمت راست توزیع سمت چپ را منعکس می کند.

توزیع گاوسی و قانون سه–انحراف معیار

بر أساس CLT، یک نمونه بزرگ دارای توزیع نرمال (توزیع گاوسی) است. این توزیع، متقارن است و دارای یک منحنی زنگی شکل است که در آن میانگین، میانه و مد منطبق هستند. یکی از ویژگی های توزیع نرمال، قانون سه سیگما در مورد مساحت زیر منحنی (Area Under the Curve: AUC) است که بیان می کند:

AUC بین -1و 1 برابر انحراف استاندارد 68.27٪ است.
AUC بین -2 و 2 برابر انحراف استاندارد 95.54٪ است.
AUC بین -3 و 3 برابر انحراف استاندارد 99.73٪ است.

این مفهوم برای محاسبه احتمال وقوع یک مقدار در این توزیع گسترش می‌یابد که منجر به آزمون‌های فرضی مانند آزمون z می‌شود.

آزمون فرض

آزمون فرض یک جنبه اساسی آمار استنباطی است و همانطور که از نام آن پیداست، برای بررسی اینکه آیا فرضی که در مورد جمعیت مطرح می‌شود درست است یا خیر استفاده می‌شود. این آزمون، اغلب با محاسبه احتمال وقوع یک مقدار در نمونه جامعه و در نظر گرفتن انحراف معیار داده ها انجام می‌شود.

عنوان تبلیغ: تسلط بر آزمون فرض در پایتون برای علم داده

آمار

مقادیر محاسباتی خاصی که به تعریف جمعیت کمک می کنند به عنوان پارامتر شناخته می شوند. با این حال، همانطور که اغلب از نمونه ها استفاده می ‌شود، این مقادیر زمانی که با استفاده از یک نمونه محاسبه می شوند، به عنوان آمار شناخته می شوند. به عنوان مثال، اگر درآمد همه هندی ها را بدانید و میانگین درآمد را از این داده های جمعیت محاسبه کنید، این مقدار یک پارامتر خواهد بود. با این حال، هنگامی که با استفاده از نمونه ی جامعه محاسبه می شود، میانگین به عنوان یک آمار شناخته می شود. برای اطمینان از اینکه میانگین نمونه واقعاً نشان‌دهنده میانگین جامعه است و ناشی از شانس تصادفی نیست، از مفهوم آزمون فرض استفاده می‌شود.

با مفاهیم مهم ارائه شده، اکنون می توانید به این سوال پاسخ دهید: آزمون پارامتریک چیست؟

آزمون‌های پارامتریک

آزمون پارامتریک در آمار به یک نوع فرعی از آزمون فرض اشاره دارد. آزمون فرض پارامتریک رایج ترین نوع آزمونی است که برای درک ویژگی های جامعه از یک نمونه انجام می‌شود. در حالی که آزمون‌های پارامتریک زیادی وجود دارد و تفاوت‌های خاصی با هم دارند، بعضی از ویژگی‌ها در تمام آزمون‌ها مشترک هستند که آنها را به بخشی از "آزمون‌های پارامتریک" تبدیل می‌کند. این ویژگی‌ها عبارتند از:

هنگام استفاده از چنین آزمون هایی، باید درک عمیق و درستی از جمعیت وجود داشته باشد.
بسط نکته فوق این است که برای استفاده از چنین آزمون‌هایی، چندین فرض در مورد جامعه باید برآورده شوند (از این رو درک صحیح جامعه مورد نیاز است). یک فرض رایج این است که جمعیت باید به طور نرمال توزیع شود.
اگر مفروضات مربوط به جمعیت به طور معنی‌داری انحراف داشته باشند، نمی‌توان به خروجی های چنین آزمون هایی اعتماد کرد.
برای اجرای چنین آزمون‌هایی به حجم نمونه بزرگی نیاز است. از نظر تئوری، حجم نمونه باید بیش از 30 باشد تا قضیه حد مرکزی بتواند اعمال شود و نمونه به طور نرمال توزیع شود. البته توجه داشته باشید که آزمون‌های پارامتریک با توزیع اریب و غیرنرمال به خوبی انجام می شوند، مشروط بر اینکه شرایط اندازه نمونه برای آزمون را برآورده کنند. (به عنوان مثال، یک آزمون t تک نمونه ای مستلزم آن است که حجم نمونه بیشتر از 20 باشد).
آزمون های پارامتریک در مقایسه با همتایان غیر پارامتریک خود برای اندازه نمونه مشابه، معمولاً قدرت آماری بیشتری دارند.
این آزمون‌ها فقط برای متغیرهای پیوسته/کمی مفید هستند.
اندازه گیری گرایش مرکزی (یعنی ارزش مرکزی داده ها) معمولاً با استفاده از میانگین انجام می شود.
خروجی چنین آزمون‌هایی به راحتی قابل تفسیر است. با این حال، درک عملکرد آنها می تواند چالش برانگیز باشد.
تست‌های پارامتریک زمانی که گستردگی (spread) هر گروه متفاوت است، عملکرد خوبی دارند. در حالی که آزمون‌های غیرپارامتریک نرمال بودن را در نظر نمی‌گیرند، اما برخی نیاز دارند که همه گروه‌هایی که مقایسه می‌شوند دارای یک گسترش باشند. این برای تست های پارامتریک مورد نیاز نیست.

برای درک نقش آزمون‌های پارامتریک در آمار، اجازه دهید انواع مختلف آزمون های پارامتریک را بررسی کنیم. این آزمون‌ها، می‌توانند یکی مسائل زیر را حل ‌کنند:

محاسبه فاصله اطمینان جمعیت با استفاده از انحراف معیار
مقایسه میانگین نمونه با یک مقدار فرضی
مقایسه دو مقدار کمی که از یک موضوع مشترک به دست آمده‌اند
مقایسه دو مقدار کمی که از دو یا چند موضوع متفاوت به دست آمده‌اند
محاسبه سطح ارتباط بین دو ویژگی عددی

آزمون z

(Z-Test)

هنگامی که شما نیاز به مقایسه میانگین نمونه با مقدار فرضی دارید (که اغلب به میانگین جامعه اشاره دارد)، از یک آزمون z استفاده می شود.

آزمون الزامات عمده ای دارد، برای مثال حجم نمونه باید بیش از 30 باشد و انحراف معیار جامعه باید مشخص باشد.

آزمون t یک نمونه

(One Sample t-Test)

اگر یکی از الزامات ذکر شده در بالا برآورده نشد، می‌توانید از نوع دیگری از آزمون پارامتریک به نام آزمون t تک نمونه ای استفاده کنید.

در اینجا اگر حجم نمونه حداقل بیشتر از 15 باشد و انحراف معیار نمونه مشخص باشد، می توانید از این آزمون استفاده کنید. در اینجا توزیع نمونه باید تقریباً نرمال باشد

آزمون t زوجی (وابسته)

(Paired (dependent) t-Test)

از آزمون t زوجی زمانی استفاده می شود که از یک موضوع، داده‌های متفاوت جمع آوری می‌شود، به طور معمول قبل و بعد از یک رویداد - به عنوان مثال، وزن یک گروه ۱۰ نفری از ورزشکاران، قبل و بعد از یک برنامه رژیم غذایی.

در اینجا برای مقایسه میانگین گروه قبل و بعد می‌توانید از آزمون t زوجی استفاده کنید. مفروضات در اینجا شامل مستقل بودن گروه ها، تعلق مقادیر به موضوع مشابه است، و همچنین تفاوت بین گروه ها باید به طور نرمال توزیع شود.

آزمون t غیر زوجی (مستقل)

(Two Sampled (Independent) t-Test)

در شرایطی که دو نمونه ی جداگانه وجود دارد، به عنوان مثال، قیمت خانه در بمبئی در مقابل قیمت خانه در دهلی و شما باید بررسی کنید که آیا میانگین هر دو نمونه از نظر آماری تفاوت معنی‌داری ندارد، آنگاه می‌توان یک آزمون t دو نمونه استفاده کرد.

فرض بر این است که توزیع داده‌های هر نمونه باید نرمال باشند، مقادیر باید پیوسته باشند، واریانس باید در هر دو نمونه برابر باشد، و آنها باید مستقل از یکدیگر باشند.

تحلیل واریانس یک طرفه (ANOVA)

(One-way Analysis of Variance)

بسط آزمون t ، آزمون ANOVA یک طرفه است که در آن بیش از دو گروه را با هم مقایسه می کنیم. فرض کنید شخصی از شما بپرسد که آیا آنالیز واریانس ، یک آزمون پارامتریک است؟ پاسخ آن یک بله قطعی است.

ANOVA واریانس گروه ها را تجزیه و تحلیل می کند و نیاز دارد که توزیع جمعیت نرمال، واریانس همگن و گروه ها مستقل باشند.

ضریب همبستگی پیرسون

(Pearson’s Coefficient of Correlation)

برای درک ارتباط بین دو متغیر عددی پیوسته، می‌توانید از ضریب همبستگی استفاده کنید.

این آزمون، یک مقدار r تولید می کند که در آن مقدار نزدیک به 1- و 1 به ترتیب نشان دهنده یک همبستگی قوی منفی و مثبت است.

مقدار نزدیک به 0 نشان دهنده عدم همبستگی بین متغیرها است. فرض این آزمون این است که هر دو متغیر باید پیوسته باشند.

آزمون های غیر پارامتریک

موقعیتی را در نظر بگیرید که نمی‌توانید فرض‌های لازم برای استفاده از آزمون فرض پارامتریک را برآروده کنید. این فرض می‌تواند به عنوان مثال در مورد حجم نمونه باشد و در حال حاضر هیچ کاری نمی توانید در مورد آن انجام دهید. حال، آیا این بدان معناست که شما نمی‌توانید با استفاده از داده ها هیچ تحلیل استنباطی انجام دهید؟ پاسخ خیر است.

در آزمون فرض، نوع دیگری از آزمون به نام آزمون غیرپارامتریک وجود دارد. از آنجایی که هر آزمون پارامتریک یک معادل غیرپارامتریک دارد، استفاده از فقط آزمون‌های غیرپارامتریک می تواند وسوسه انگیز باشد. همچنین، آنها فرضیات کمتری در مورد توزیع و پارامترهای جمعیت مورد نظر دارند و در شرایطی که فرض‌های پارامتریک برآورده نشود، به راحتی قابل استفاده هستند. البته توجه کنید که آزمون‌های غیرپارامتریک معایبی نیز دارند.

اولین مورد این است که آزمون های غیرپارامتریک در مقایسه با معادل پارامتریک خود از نظر آماری قدرت کمتری دارند. قدرت آماری احتمال این است که آزمون ها به ما اجازه می دهند که فرض صفر را در صورت نادرست بودن رد کنیم. زمانی که فرض صفر نادرست باشد، تصمیم گیری صحیح است. به بیان ساده، قدرت آماری احتمال عدم ایجاد خطای نوع II است. آزمون های پارامتریک به سادگی از نظر آماری قدرتمندتر هستند. آزمون های غیرپارامتریک به اندازه نمونه کمی بزرگتر نیاز دارند تا قدرت آماری مشابهی با همتای پارامتریک خود داشته باشند.

دومین مورد این است که نتایج آزمون های غیرپارامتریک کمتر قابل تفسیر هستند. بسیاری از آزمون‌های غیرپارامتریک از رتبه بندی مقادیر در داده‌ها به جای داده‌های واقعی استفاده می کنند و این ممکن است به اندازه کار با داده‌های واقعی قابل درک نباشد.

هنگامی که داده‌های شما اجازه می دهد، بهتر است از یک آزمون پارامتریک استفاده کنید. آزمون‌های غیرپارامتریک کاربردهای خود را دارند اما باید آنها را با دقت در نظر بگیرید. می‌توان دلایل زیر را برای استفاده از این آزمون‌های غیرپارامتریک بیان کرد:

آزمون های غیرپارامتریک زمانی معتبر هستند که داده ها با مفروضات مرتبط با آزمون پارامتریک مورد نظر مطابقت نداشته باشند.
آزمون‌های غیرپارامتریک اغلب گزینه خوبی برای نمونه‌های کوچک هستند که در آن نگرانی در مورد مفروضات نرمال بودن آزمون پارامتریک وجود دارد.
زمانی می توان از آزمون های غیرپارامتریک استفاده کرد که حوزه مطالعه به بهترین وجه با میانه نمایش داده شود.
از آزمون‌های غیرپارامتریک می‌توان برای تجزیه و تحلیل داده‌های ترتیبی، داده‌های رتبه‌بندی شده یا زمانی که نمی‌توان مقادیر پرت را از داده‌ها حذف کرد، استفاده کرد.

در بخش قبل، چندین آزمون پارامتریک بیان شد که می توانند انواع مختلف مسائل استنباطی آماری را حل کنند. انواع متداول آزمون های غیرپارامتریک معادل با آن‌ها عبارتند از:

آزمون رتبه‌ای علامت دار ویلکاکسون

(Wilcoxon signed-rank test)

این روش، جایگزین آزمون پارامتریک - آزمون t زوجی است

آزمون یو من ویتنی / آزمون جمع رتبه‌ای ویلکاکسون

(Mann-Whitney U-test / Wilcoxon rank-sum test)

این روش جایگزین آزمون t دو نمونه است

آزمون کروسکال والیس

(Kruskal-Wallis test)

این روش جایگزین آزمون پارامتریک - ANOVA یک طرفه است

همبستگی رتبه اسپیرمن

(Spearman’s rank correlation)

می توانید از این آزمون به عنوان جایگزینی برای ضریب همبستگی پیرسون استفاده کنید.

جایگزین‌هایی برای تمام تست های پارامتریک وجود دارد. بنابراین، اگر نمی‌توانید هیچ فرضی را برآورده کنید، می‌توانید از آزمون‌های غیرپارامتریک مربوطه استفاده کنید.

آزمون پارامتریک در مقابل غیر پارامتریک

پس از کاوش در آزمون‌های پارامتریک و غیر پارامتریک، اکنون زمان آن رسیده که تفاوت های آنها را خلاصه کنیم. جدول زیر می‌تواند به شما در درک زمان و مکان استفاده از آزمون‌های پارامتریک یا همتایان غیرپارامتریک آنها و همچنین مزایا و معایب آنها کمک کند.

معیار	پارامتریک	غیر پارامتریک
جمعیت	درک درستی از جمعیت در دسترس است	اطلاعات زیادی در مورد جمعیت در دسترس نیست
مفروضات	چندین فرض در مورد جمعیت وجود دارد. در صورت عدم تحقق مفروضات، نتایج نادرستی ارائه می‌شود	هیچ فرضی در مورد جمعیت وجود ندارد
توزیع	لازم است توزیع جمعیت نرمال باشد	نیازی به نرمال بودن جمعیت ندارد. می تواند دلخواه باشد.
حجم نمونه	حجم نمونه باید بیش از 30 باشد	می تواند با نمونه‌های کوچک کار کند
تفسیر پذیری	به راحتی قابل تفسیر هستند	تفسیر آنها دشوار است
پیاده سازی	به سختی اجرا می شوند	به راحتی قابل اجرا هستند
قابلیت اطمینان	خروجی قدرتمندتر/قابل اعتمادتر است	قدرت/ قابلیت اعتماد خروجی کمتر است
نوع متغیر	با متغیرهای پیوسته/ کمی کار می‌کنند	با متغیرهای پیوسته/کمی و همچنین طبقه‌ای/گسسته کار می‌کنند
گرایش مرکزی	اندازه گیری گرایش مرکزی معمولاً با استفاده از میانگین انجام می‌شود	اندازه گیری گرایش مرکزی به طور کلی با استفاده از میانه انجام می‌شود
نقاط پرت	تحت تأثیر نقاط پرت است	کمتر تحت تأثیر نقاط پرت قرار می‌گیرد
فرض صفر	دقیق تر	فرض صفر را به اشتباه رد می کند. دقت کمتری دارد
انواع آزمون‌ها	z-test, t-test, ANOVA, f-test, Pearson coefficient of correlation	One sample KS test, Wilcoxon signed rank test, Mann-Whitney U-test, Wilcoxon rank-sum test, Wilcoxon signed-rank test, Kruskal-Wallis test, Spearman's rank correlation, Kuiper's test, Hosmer-Lemeshow test, Chi-Square test for independence

اکنون شما درک بهتری از تفاوت بین آزمون های پارامتریک و غیرپارامتریک دارید و می‌توانید از نوع آزمونی که متناسب با نیاز شماست و می تواند بهترین نتایج را برای شما ارائه دهد استفاده کنید.

آزمون پارامتریک یا غیر پارامتریک: از کدام یک برای آزمون فرض استفاده کنیم؟