در یادگیری ماشین، پایه و اساس مدلسازی موفق بر روی کیفیت دادههایی است که با آنها آموزش دیدهاند و در حالی که کانون توجه، اغلب بر روی الگوریتمها و مدلهای پیچیده و پیچیدهتر است، قهرمان گمنام پیشپردازش دادهها است.
پیش پردازش دادهها مانند بسترسازی برای یک ساختمان محکم است و در این زمینه، یکی از جنبههایی که اغلب نادیده گرفته میشود، مقیاسبندی ویژگیها (Feature Scaling) در مجموعه داده است.
هدف از مقیاسبندی ویژگی این است که اطمینان حاصل شود که همه ویژگیها بدون در نظر گرفتن مقیاس اصلیشان، به طور یکسان در فرآیند یادگیری مشارکت کنند. الگوریتم های یادگیری ماشین اغلب با این فرض آموزش داده میشوند که همه ویژگی ها به طور مساوی در پیش بینی نهایی نقش دارند. با این حال، زمانی که ویژگی ها در محدودهها و واحدهای متفاوت باشند، این فرض شکست می خورد.
تصور کنید مجموعه دادهای با ویژگیهایی دارید که در مقیاس های بسیار متفاوتی هستند، برای مثال سن به سال در مقابل درآمد به ده ها هزار دلار. اگر بخواهید مدلی را بدون مقیاسبندی این ویژگیها بسازید، ممکن است ناخواسته یکی از ویژگیها را صرفاً به دلیل مقیاس آن بر دیگری اولویت دهید که این منجر به انحراف نتایج میشود. به بیان ساده، این طور فکر کنید که وقتی یک آبمیوه مخلوط درست می کنید، نمی خواهید طعم یک میوه خاص بر سایر میوهها غالب شود، به همین ترتیب، در مدل یادگیری ماشین، ما نمیخواهیم ویژگی خاصی تاثیر بیشتری از بقیه داشته باشد و ما باید ویژگی ها را به گونه ای مقیاس کنیم که یک ویژگی با بزرگی زیاد بر سایر ویژگی ها تسلط پیدا نکند.
بیایید به یک مثال عینی بپردازیم تا اهمیت مقیاس بندی ویژگی را بهتر متوجه شویم. مجموعه داده ای حاوی دو ویژگی را در نظر بگیرید که "قد" با سانتی متر و "وزن" با کیلوگرم اندازه گیری می شود.

بدون مقیاسبندی ویژگی، یک الگوریتم یادگیری ماشین ممکن است تغییر یک واحدی در قد را مهمتر از تغییر یک واحدی در وزن تفسیر کند، زیرا قد معمولاً مقادیر بزرگتری از وزن دارد. در نتیجه، مدل ممکن است به اشتباه، اهمیت بیشتری به ویژگی "قد" بدهد. برای حل این مشکل، با اعمال مقیاسبندی ویژگی، هر دو ویژگی را روی یک مقیاس قرار میدهیم، معمولاً بین 0 و 1 یا با میانگین 0 و انحراف معیار 1. این مقیاسبندی تضمین میکند که هر ویژگی به طور متناسبی در فرآیند یادگیری مدل نقش داشته باشد. پس از مقیاس بندی، مجموعه داده ما به شکل زیر در میآید:

اکنون، هر دو ویژگی در موقعیت برابر قرار دارند و الگوریتم یادگیری ماشینی میتواند به طور مؤثرتری از آنها بیاموزد، بدون اینکه تحت تأثیر تفاوتهای مقیاس قرار گیرد.
بنابراین، همانطور که در این مثال دیدیم، مقیاسبندی ویژگی، رفتار منصفانه با ویژگیها را تضمین میکند و مدلها را قادر میسازد تا بر اساس اهمیت واقعی هر ویژگی پیشبینیهای دقیق انجام دهند. در واقع، ما با گنجاندن مقیاسبندی ویژگی در خط لوله یادگیری ماشین خود، راه را برای مدلهای قویتر و قابل اعتمادتر هموار میکنیم تا بتوانند مجموعه دادههای متنوع را با دقت بیشتر، مدیریت و مدل کند.
چه زمانی مقیاس بندی ویژگی را باید انجام دهیم؟
اولین سوالی که می خواهیم به آن بپردازیم این است که چه زمانی باید متغیرهای موجود در مجموعه داده خود را مقیاس بندی کنیم؟ برخی از الگوریتمهای یادگیری ماشین به مقیاسبندی ویژگی حساس هستند، در حالی که برخی دیگر تقریباً با مقیاسبندی ویژگی تغییر نمیکنند. بیایید آن را با جزئیات بیشتر بررسی کنیم.
الگوریتم های مبتنی بر گرادیان کاهشی (Gradient Descent Based Algorithms)
الگوریتمهای یادگیری ماشین مانند رگرسیون خطی، رگرسیون لجستیک، شبکه عصبی و غیره که از گرادیان کاهشی به عنوان یک تکنیک بهینهسازی استفاده میکنند، به مقیاسبندی دادهها نیاز دارند. به فرمول گرادیان کاهشی زیر نگاهی بیندازید: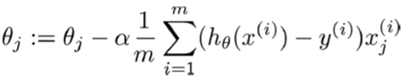
وجود مقدار ویژگی x در این فرمول بر اندازه گام کاهش گرادیان تأثیر می گذارد. تفاوت در دامنه ویژگی ها باعث می شود که اندازه گام های مختلف برای هر ویژگی متفاوت باشد. برای اطمینان از اینکه گرادیان کاهشی به آرامی به سمت حداقل حرکت می کند و مراحل کاهش گرادیان با سرعت یکسان برای همه ویژگی ها به روز می شوند، داده ها را قبل از دادن به مدل باید مقیاس کنیم. در واقع، داشتن ویژگی هایی در مقیاس مشابه می تواند به کاهش گرادیان کمک کند تا سریعتر به سمت حداقل همگرا شود.
در مورد الگوریتمهای شبکههای عصبی، مقیاسبندی ویژگیها مزایای زیر را برای بهینهسازی ایجاد میکند:
- باعث می شود که آموزش سریعتر شود
- از گیر افتادن بهینه سازی در بهینه محلی جلوگیری می کند
- سطح خطای بهتری می دهد
- کاهش وزن و بهینه سازی Bayes را می تواند راحت تر انجام دهد
الگوریتم های مبتنی بر فاصله (Distance-Based Algorithms)
الگوریتم های مبتنی بر فاصله مانند KNN، K-means و SVM بیشتر تحت تاثیر دامنه ویژگی ها هستند و این به این دلیل است که آنها در پشت صحنه از فاصله بین نقاط داده برای تعیین شباهت آنها استفاده می کنند. برای مثال، فرض کنید ما دادههایی داریم که شامل نمرات CGPA دبیرستانی دانشآموزان (از 0 تا 5) و درآمدهای آینده آنها (به هزار روپیه) است:
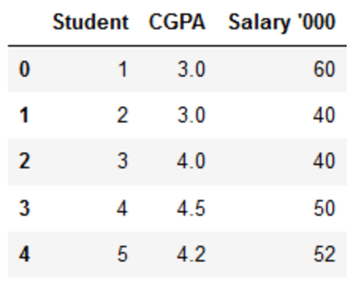
از آنجایی که هر دو ویژگی دارای مقیاسهای متفاوتی هستند، این احتمال وجود دارد که وزن بیشتری به ویژگیهایی با مقدار بالاتر داده شود، که این بر عملکرد الگوریتم یادگیری ماشین تأثیر می گذارد و بدیهی است که ما نمی خواهیم الگوریتم ما نسبت به یک ویژگی تعصب داشته باشد. بنابراین، قبل از استفاده از یک الگوریتم مبتنی بر فاصله، باید دادههای خود را مقیاسبندی کنیم تا همه ویژگیها به طور مساوی در نتیجه مشارکت داشته باشند.
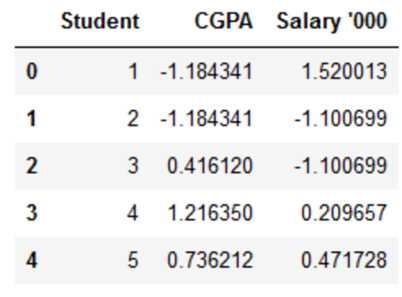
برای مثال، وقتی فاصله اقلیدسی بین نقاط داده برای دانشآموزان A و B و همچنین B و C را قبل و بعد از مقیاسبندی مانند زیر مقایسه میکنیم، تأثیر مقیاسبندی بیشتر آشکار میشود:
• فاصله AB قبل از مقیاس بندی:
• فاصله BC قبل از مقیاس بندی: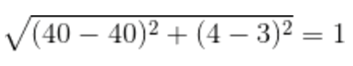
• فاصله AB بعد از مقیاس بندی: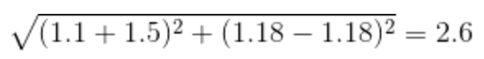
• فاصله BC بعد از مقیاس بندی: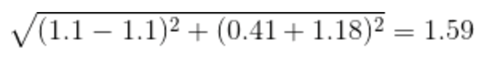
همانطور که میبینید، مقیاسبندی همهی ویژگیها را به طور یکسان به میان آورده است و هم اکنون فواصل نسبت به قبل از مقیاسبندی قابل مقایسهتر هستند.
الگوریتم های مبتنی بر درخت (Tree-Based Algorithms)
از سوی دیگر، الگوریتمهای مبتنی بر درخت نسبتاً نسبت به مقیاس ویژگیها حساس نیستند. یک درخت تصمیم تنها یک گره را بر اساس یک ویژگی واحد تقسیم می کند تا همگنی گره را افزایش دهد. بنابراین، این تقسیم در یک ویژگی تحت تأثیر سایر ویژگی ها قرار نمیگیرد و عملاً ویژگی های باقی مانده بر روی تقسیم هیچ تأثیری ندارند. این ویژگی چیزی است که درختان تصمیم را نسبت به مقیاسبندی ویژگی ها تغییرناپذیر می کند!
روشهای مقیاسبندی ویژگی
نرمالسازی یا مقیاسبندی Min-Max و نرمالسازی z-score یا استانداردسازی دو تکنیک اصلی برای مقیاسبندی دادهها هستند. غیر از این موارد، ما در مورد مقیاسبندی اعشاری (decimal)، مقیاسبندی لگاریتمی (log)، مقیاس بندی MaxAbs و مقیاسبندی منسجم (robust) هم بحث خواهیم کرد که هر کدام به چالشهای منحصربهفردی در پیشپردازش دادهها رسیدگی میکنند.
💎 برای آشنایی با تکنیکهای مقیاسبندی ویژگیها با استفاده از scikit-learn به بخش آموزشی با همین نام در دورهی آموزش یادگیری نظارت شده با کتابخانه sickt-learn مراجعه کنید.
نرمالسازی یا مقیاسبندی Min-Max
نرمالسازی یک تکنیک مقیاسبندی است که در آن مقادیر شیفت داده میشوند و مجدداً مقیاس میشوند تا در نهایت بین ۰ و ۱ قرار بگیرند. به نرمالسازی، مقیاسبندی Min-Max نیز گفته میشود و فرمول آن به شکل زیر است: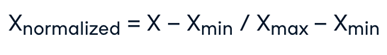
در اینجا، Xmax و Xmin به ترتیب حداکثر و حداقل مقادیر ویژگی هستند.
- وقتی مقدار X حداقل مقدار در ستون باشد، صورت کسر ۰ میشود و بنابراین Xnormalized برابر صفر خواهد شد.
- از طرف دیگر، زمانی که مقدار X حداکثر مقدار در ستون باشد، صورت برابر با مخرج خواهد شد و بنابراین مقدار Xnormalized برابر با یک خواهد شد.
- اگر مقدار X بین حداقل و حداکثر مقدار باشد، مقدار Xnormalized بین 0 و 1 خواهد شد.
پیادهسازی در پایتون:
from sklearn.preprocessing import MinMaxScaler
norm = MinMaxScaler().fit(data)
transformed_data = norm.transform(data)نرمالسازی z-score یا استانداردسازی
استانداردسازی (یا نرمالسازی z-score) یکی دیگر از تکنیک های مقیاسبندی است که در آن مقادیر حول میانگین ۰ با انحراف معیار یک (μ=0 و σ=1) متمرکز می شوند. این بدان معنی است که میانگین ویژگی صفر میشود و توزیع حاصل دارای انحراف معیار واحد است. فرمول استانداردسازی به صورت زیر است:
که در آن، μ میانگین مقادیر ویژگی و σ انحراف معیار مقادیر ویژگی است. توجه داشته باشید که در این مورد، همه مقادیر به یک محدوده خاص محدود نمی شوند (در واقع، حدود 68 درصد از مقادیر بین ۱- و ۱ قرار خواهند گرفت).
پیادهسازی در پایتون:
from sklearn.preprocessing import StandardScalerscale
StandardScaler().fit(data)
scaled_data = scale.transform(data)حال، قبل از اینکه به سایر تکنیکهای مقیاسبندی دادهها بپردازیم، بیاید به سوال مهمی که در ذهن شما احتمالا به وجود آمده است، پاسخ دهیم: این که چه زمانی باید از نرمال سازی و چه زمانی از استانداردسازی استفاده کنیم؟ برای پاسخ به این سوال، اجازه دهید مقایسه نرمالسازی و استانداردسازی را انجام دهیم.
سوال مهم – نرمالسازی یا استاندارد سازی؟
نرمال سازی در مقابل استانداردسازی یک سوال همیشگی در میان تازه واردان یادگیری ماشین است. در حالی که هیچ پاسخ واضحی برای این سوال وجود ندارد و پاسخ آن واقعاً به کاربرد بستگی دارد، هنوز چند اصل کلی وجود دارد که می توان آنها را در نظر گرفت . بیایید آنها را بررسی کنیم.
- وقتی می دانید که توزیع داده های شما از توزیع گاوسی پیروی نمی کند، از نرمال سازی استفاده میشود. این روش می تواند در الگوریتم هایی که هیچ توزیعی را برای دادهها فرض نمی کنند مفید باشد مانند K-Nearest Neighbors و Neural Networks. الگوریتمهای شبکه عصبی که به داده ها در مقیاس ۰-۱ نیاز دارند، نرمالسازی یک مرحله پیش پردازش ضروری است. یکی دیگر از نمونههای محبوب نرمالسازی دادهها، پردازش تصویر است، که در آن شدت پیکسلها باید نرمال شوند تا در محدوده خاصی قرار بگیرند (یعنی ۰ تا ۲۵۵ برای محدوده رنگ RGB).
- از سوی دیگر، استانداردسازی در مواردی که داده ها از توزیع گاوسی پیروی می کنند میتواند مفید باشد. با این حال، این لزوماً همیشه ممکن است درست نباشد. همچنین، بر خلاف روش نرمالسازی، استانداردسازی محدوده مرزی ندارد. بنابراین، حتی اگر در دادههای خود پرت داشته باشید، تحت تأثیر استانداردسازی قرار نخواهند گرفت.
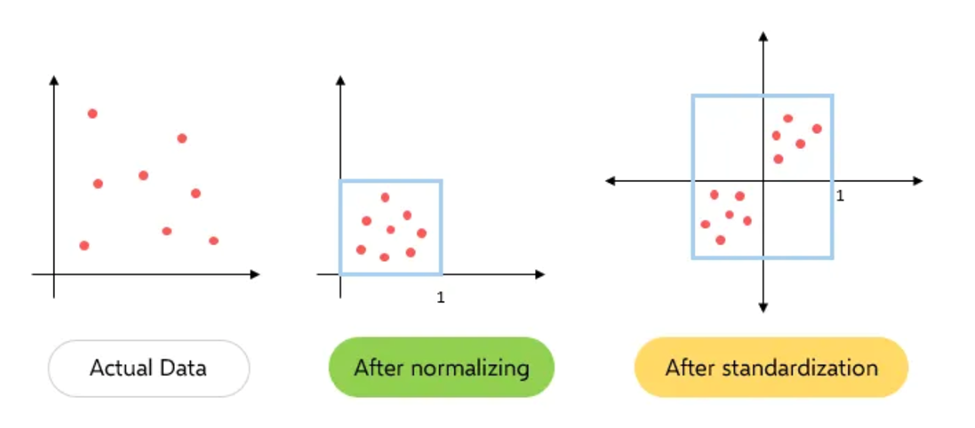
در کل، انتخاب استفاده از نرمال سازی یا استانداردسازی به مسئله شما و الگوریتم یادگیری ماشینی که استفاده می کنید بستگی دارد و هیچ قانون سخت و سریعی وجود ندارد که به شما بگوید چه زمانی باید داده های خود را نرمال یا استاندارد کنید. شما همیشه می توانید با فیت کردن مدل خود با داده های خام، نرمالسازی و استاندارد سازی را شروع کنید و عملکرد را برای رسیدن به بهترین نتایج مقایسه کنید.
بهتر است که همیشه مقیاسبندی را روی دادههای آموزشی انجام دهید و سپس از آن روش، برای تبدیل دادههای آزمایشی استفاده کنید. این امر از هرگونه نشت داده در طول فرآیند آزمایش مدل جلوگیری می کند. همچنین، مقیاس بندی مقادیر هدف معمولاً مورد نیاز نیست.
نرمالسازی | استانداردسازی |
هدف این است که مقادیر یک ویژگی را در یک محدوده خاص، اغلب بین ۰ و ۱ قرار دهیم | هدف این است که مقادیر یک ویژگی را تبدیل کنیم تا میانگین ۰ و انحراف معیار ۱ داشته باشند |
حساس به نقاط پرت و محدوده داده ها | به دلیل استفاده از میانگین و انحراف معیار، حساسیت کمتری نسبت به نقاط پرت دارد |
زمانی مفید است که محدوده اصلی دادهها باید حفظ شود | زمانی موثر است که الگوریتمها توزیع نرمال استاندارد را در نظر میگیرند |
هیچ فرضی در مورد توزیع داده ها وجود ندارد | توزیع نرمال یا تقریب نزدیک به آن را فرض می کند |
برای الگوریتم هایی که مقادیر مطلق و روابط آنها مهم است، برای مثال، -kنزدیک ترین همسایه، شبکه های عصبی مناسب است | برای الگوریتمهایی که توزیع دادهها را نرمال فرض میکنند، مانند رگرسیون خطی و ماشینهای بردار پشتیبان مفید است |
قابلیت تفسیر مقادیر اصلی را در محدوده مشخص شده حفظ می کند | مقادیر اصلی را تغییر می دهد و به دلیل تغییر در مقیاس و واحدها، تفسیر را چالش برانگیز می کند |
می تواند منجر به همگرایی سریعتر شود، به خصوص در الگوریتم هایی که بر کاهش گرادیان متکی هستند | به همگرایی سریعتر کمک می کند، به ویژه در الگوریتم های حساس به مقیاس ویژگی های ورودی |
موارد استفاده: پردازش تصویر، شبکه های عصبی، الگوریتم های حساس به مقیاس های ویژگی | موارد استفاده: رگرسیون خطی، ماشین های بردار پشتیبان، الگوریتم هایی با فرض توزیع نرمال |
مقیاسبندی اعشاری (Decimal)
هدف مقیاسبندی Decimal این است که مقادیر ویژگیها را با توان ۱۰ مقیاس کنیم و اطمینان حاصل کنیم که بزرگترین قدر مطلق در هر ویژگی کمتر از ۱ میشود. به عبارتی، مقیاسبندی اعشاری با جابجایی نقطه اعشار در مقدار، مقدار ویژگی A را نرمال می کند و این جابهجایی نقطه اعشار به حداکثر مقدار مطلق ویژگی بستگی دارد. این روش، زمانی مفید است که محدوده مقادیر در یک مجموعه داده مشخص باشد، اما محدوده های متفاوت وجود داشته باشند. فرمول مقیاسبندی اعشاری به صورت زیر است: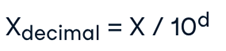
که در آن، X مقدار ویژگی اصلی است و d کوچکترین عدد صحیحی است که بر اساس آن، بزرگترین قدر مطلق در ویژگی کمتر از ۱ شود. به عنوان مثال، فرض کنید مقادیر مشاهده شده برای ویژگی A در محدوده ۹۸۶- تا ۹۱۷ قرار دارند. بنابراین، حداکثر مقدار مطلق برای ویژگی A برابر ۹۸۶ است. در اینجا، برای مقیاسبندی هر مقدار از ویژگی A با استفاده از مقیاس بندی اعشاری ، ما باید هر مقدار مشخص A را بر 1000 یعنی ۳=d تقسیم کنیم. بنابراین، مقدار ۹۸۶- به ۰.۹۸۶- و ۹۱۷ به ۰.۹۱۷ نرمال می شود.
توجه کنید که مقیاس بندی اعشاری زمانی سودمند است که ما با مجموعه داده هایی سروکار داریم که در آن قدرمطلق مقادیر بیشتر از مقیاس آنها اهمیت دارد.
مقیاسبندی لگاریتمی
مقیاسبندی لگاریتمی، با گرفتن لگاریتم هر نقطه داده، دادهها را به مقیاس لگاریتمی تبدیل میکند. این روش وقتی ویژگیهایی با واریانس بالا داریم میتواند مفید باشد. فرمول مقیاسبندی لگاریتمی به صورت زیر است: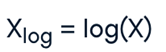
روش مقیاسبندی لگاریتمی برای داده هایی که رشد یا نزول تصاعدی دارند، مفید است زیرا مقیاس مجموعه داده را فشرده می کند و تشخیص الگوها و روابط در داده ها را برای مدل ها آسان تر می کند. تغییر اندازه جمعیت در طی سالها نمونه خوبی از مجموعه دادهای است که در آن برخی از ویژگیها رشد تصاعدی را نشان میدهند. مقیاسبندی لگاریتمی میتواند این ویژگیها را برای مدلسازی سازگارتر کند.
مقیاسبندی MaxAbs
در MaxAbs Scaler هر ویژگی با استفاده از حداکثر مقدار خود مقیاس بندی می شود. در ابتدا مقدار حداکثر مطلق ویژگی پیدا می شود و سپس مقادیر ویژگی با آن تقسیم می شوند. درست مانند MinMaxScaler MaxAbs Scaler نیز به نقاط پرت حساس هستند.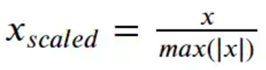
پیادهسازی در پایتون:
from sklearn.preprocessing import MaxAbsScaler()
maxabs = MaxAbsScaler ().fit(data)
data_norm = maxabs.transform(data(مقیاسبندی منسجم (Robust)
مقیاس بندی منسجم هنگام کار با مجموعه داده هایی که دارای مقادیر پرت هستند مفید است. این روش، به جای میانگین و انحراف معیار برای رسیدگی به نقاط پرت، از میانه و محدوده و بین چارکی (IQR) استفاده می کند. فرمول مقیاس بندی منسجم به صورت زیر است:

از آنجایی که مقیاس بندی منسجم در برابر نقاط پرت انعطاف پذیر است، برای مجموعه داده هایی با مقادیر کج (skewed) یا غیرعادی مناسب است.
پیادهسازی در پایتون:
from sklearn.preprocessing import RobustScaler
rob = RobustScaler().fit(data)
data_norm = rob.transform(data(چالشهای مقیاسبندی
ما در مورد مقیاسبندی و اینکه چرا در یادگیری ماشین مفید است بحث کردیم. مقیاسبندی اگرچه قدرتمند است، اما بدون چالش نیست. از رسیدگی به نقاط پرت گرفته تا انتخاب مناسبترین تکنیک بر اساس مجموعه دادههای شما، پرداختن به این مسائل برای آزادسازی پتانسیل کامل مدل یادگیری ماشین ضروری است.
رسیدگی به نقاط پرت
نقاط پرت، نقاط دادهای در مجموعه داده هستند که به طور قابل توجهی از مقدار نرمال دادهها دور هستند و اثربخشی تکنیک های مقیاسبندی را مخدوش می کنند. عدم مدیریت نقاط پرت در دادهها میتواند منجر به ایجاد تبدیلهای skewed شود. برای حل این مشکل میتوانید با تکنیک مقیاسپذیری منسجم (robust) که قبلاً در مورد آن صحبت کردیم، رسیدگی به نقاط پرت را کنترل کنید.
استراتژی دیگر استفاده از trimming یا winsorizing است، که در آن همه مقادیر ویژگی که بالا (یا پایین) مقدار مشخصی هستند، را به یک مقدار ثابت محدود میکنیم.
انتخاب تکنیک مقیاسبندی
ما مفیدترین تکنیک های مقیاسبندی را مورد بحث قرار دادیم، اما روش های بسیار بیشتری برای انتخاب وجود دارد. انتخاب تکنیک مناسب، نیاز به درک دقیق مجموعه داده دارد. هنگام پیش پردازش داده ها، باید چندین تکنیک مقیاسبندی را امتحان کنید و تأثیر آنها را بر عملکرد مدل ارزیابی کنید. آزمایش به شما امکان می دهد مشاهده کنید که چگونه هر روش بر فرآیند یادگیری تأثیر می گذارد.
شما باید درک عمیقی از ویژگی های داده به دست آورید. در نظر بگیرید که آیا مفروضات یک تکنیک مقیاسبندی خاص با توزیع و الگوهای موجود در مجموعه داده مطابقت دارد یا خیر.
مقیاسبندی داده های پراکنده
زمانی که با داده های پراکنده سروکار داریم که در آنها بسیاری از مقادیر ویژگی صفر هستند، مقیاسبندی میتواند چالش برانگیز باشد. استفاده مستقیم از تکنیک های نرمالسازی یا استانداردسازی ممکن است منجر به عواقب ناخواسته شود. نسخههایی از تکنیکهای مقیاسبندی وجود دارد که در بالا مورد بحث قرار دادیم که بهطور خاص برای دادههای پراکنده طراحی شدهاند، مانند ‘sparse min-max scaling’.
قبل از مقیاسبندی، مقادیر گمشده را در مجموعه دادههای خود impute یا مدیریت کنید. این کار اغلب یکی از اولین گامهایی است که در هنگام بررسی مجموعه دادههای خود و تمیز کردن آن برای استفاده در مدلهای یادگیری ماشین باید انجام دهید.
مقیاسبندی و خطر بیش برازشی
در یادگیری ماشین، بیش برازشی زمانی اتفاق میافتد که یک مدل نه تنها الگوهای اصلی در دادههای آموزشی را یاد میگیرد، بلکه نویز و نوسانات تصادفی را نیز ثبت میکند. این کار میتواند منجر به مدلی شود که عملکرد فوقالعادهای روی دادههای آموزشی دارد، اما نمیتواند به دادههای جدید و نادیده تعمیم یابد.
مقیاسبندی به تنهایی ممکن است باعث بیش برازشی نشود. با این حال، هنگامی که مقیاسبندی با عوامل دیگر، مانند پیچیدگی مدل یا تنظیم (regularization) ناکافی ترکیب شود، می تواند باعث بیش برازشی شود. هنگامی که پارامترهای مقیاسبندی با استفاده از کل مجموعه داده (شامل اعتبارسنجی یا مجموعه های آزمایشی) محاسبه می شوند، می تواند منجر به نشت داده (data leakage) شود. این مدل ممکن است به طور ناخواسته اطلاعاتی را از اعتبارسنجی یا مجموعه های آزمایشی بیاموزد و توانایی آن را برای تعمیم به خطر بیندازد.
بنابراین، برای کاهش خطر بیش برازشی، بهتر است ابتدا مجموعه آموزشی را مقیاسبندی کنید و سپس پارامترهای مقیاسبندی بدست آمده را در مجموعه های اعتبارسنجی و آزمایشی اعمال کنید. این کار تضمین میکند که مدل یاد میگیرد که فراتر از دادههای آموزشی تعمیم یابد، بدون اینکه تحت تأثیر اطلاعات موجود در مجموعههای آزمایشی یا اعتبارسنجی قرار گیرد.
برای جریمه کردن مدل های بیش از حد پیچیده باید تکنیک های تنظیم (regularization) مناسب را پیاده سازی کنید. تنظیم از فیت شدن مدل به نویز در دادههای آموزشی جلوگیری میکند. برای ارزیابی عملکرد مدل بر روی دادههای دیده نشده، از تکنیکهای اعتبارسنجی مناسب مانند اعتبارسنجی متقابل استفاده کنید. اگر در طول اعتبارسنجی بیش برازشی تشخیص داده شود، می توان تنظیماتی مانند کاهش پیچیدگی مدل یا افزایش تنظیم را انجام داد.
استفاده از مقیاسبندی در الگوریتمهای یادگیری ماشین
اکنون زمان آن رسیده است که برخی از الگوریتمهای یادگیری ماشین را روی دادههای خود آموزش دهیم تا اثرات تکنیکهای مختلف مقیاسبندی را بر روی عملکرد الگوریتمها، مقایسه کنیم. بیایید اثر مقیاسبندی را روی سه الگوریتم ویژه ببینیم: K- نزدیکترین همسایهها، رگرسیون پشتیبان بردار (SVR)، و درخت تصمیم.
k-نزدیکترین همسایه
همانطور که قبلا دیدیم، KNN یک الگوریتم مبتنی بر فاصله است که تحت تأثیر دامنه ویژگی ها قرار می گیرد. بیایید ببینیم که چگونه بر روی دادههای ما، قبل و بعد از مقیاسبندی عمل میکند:
# training a KNN model
from sklearn.neighbors import KNeighborsRegressor
# measuring RMSE score
from sklearn.metrics import mean_squared_error
# knn
knn = KNeighborsRegressor(n_neighbors=7)
rmse = []
# raw, normalized and standardized training and testing data
trainX = [X_train, X_train_norm, X_train_stand]
testX = [X_test, X_test_norm, X_test_stand]
# model fitting and measuring RMSE
for i in range(len(trainX)):
# fit
knn.fit(trainX[i],y_train)
# predict
pred = knn.predict(testX[i])
# RMSE
rmse.append(np.sqrt(mean_squared_error(y_test,pred)))
# visualizing the result
df_knn = pd.DataFrame({'RMSE':rmse},index=['Original','Normalized','Standardized'])
df_knn
می توانید ببینید که مقیاس بندی ویژگی ها، امتیاز RMSE مدل KNN را پایین آورده است. به طور خاص، دادههای نرمال شده کمی بهتر از داده های استاندارد شده عمل می کنند.
رگرسیون بردار پشتیبان
SVR یکی دیگر از الگوریتم های مبتنی بر فاصله است. بنابراین بیایید بررسی کنیم که با نرمالسازی بهتر کار می کند یا استانداردسازی.
# training an SVR model
from sklearn.svm import SVR
# measuring RMSE score
from sklearn.metrics import mean_squared_error
# SVR
svr = SVR(kernel='rbf',C=5)
rmse = []
# raw, normalized and standardized training and testing data
trainX = [X_train, X_train_norm, X_train_stand]
testX = [X_test, X_test_norm, X_test_stand]
# model fitting and measuring RMSE
for i in range(len(trainX)):
# fit
svr.fit(trainX[i],y_train)
# predict
pred = svr.predict(testX[i])
# RMSE
rmse.append(np.sqrt(mean_squared_error(y_test,pred)))
# visualizing the result
df_svr = pd.DataFrame({'RMSE':rmse},index=['Original','Normalized','Standardized'])
df_svr
میتوانیم ببینیم که مقیاسبندی ویژگیها، امتیاز RMSE را پایین میآورد و داده های استاندارد شده بهتر از داده های نرمال شده عمل کرده اند. به نظر شما چرا اینطور است؟
مستندات sklearn بیان می کند که SVM، با هسته RBF، فرض می کند که تمام ویژگی ها حول صفر هستند و واریانس از همان order است. این به این دلیل است که یک ویژگی با واریانس بیشتر از ویژگی های دیگر، برآوردگر را از یادگیری از همه ویژگی ها باز می دارد.
درخت تصمیم
همانطور که قبلا گفته شد، درخت تصمیم نسبت به مقیاس بندی ویژگی تغییرناپذیر است. حال بیایید با یک مثال عملی ،نحوه عملکرد آن را روی داده ها بررسی کنیم:
# training a Decision Tree model
from sklearn.tree import DecisionTreeRegressor
# measuring RMSE score
from sklearn.metrics import mean_squared_error
# Decision tree
dt = DecisionTreeRegressor(max_depth=10,random_state=27)
rmse = []
# raw, normalized and standardized training and testing data
trainX = [X_train,X_train_norm,X_train_stand]
testX = [X_test,X_test_norm,X_test_stand]
# model fitting and measuring RMSE
for i in range(len(trainX)):
# fit
dt.fit(trainX[i],y_train)
# predict
pred = dt.predict(testX[i])
# RMSE
rmse.append(np.sqrt(mean_squared_error(y_test,pred)))
# visualizing the result
df_dt = pd.DataFrame({'RMSE':rmse},index=['Original','Normalized','Standardized'])
df_dt
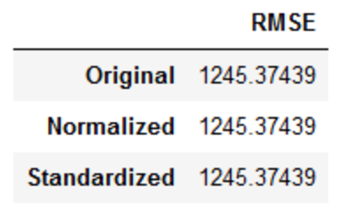
می بینید که امتیاز RMSE در مقیاسبندی ویژگیها یک اینچ هم جابجا نشده است. بنابراین وقتی از الگوریتمهای درختی بر روی داده های خود استفاده می کنید، میتواند خیالتان راحت باشد!