انواع رایج توزیع آماری داده‌ها

در مقاله‌ی راهنمایی جامع برای تسلط بر تکنیک‌های توزیع آماری داده‌ها، اصول اولیه توزیع داده‌ها و پارامترهای آنها پوشش داده شد. اکنون در این مقاله برخی از رایج‌ترین این توزیع ها را به همراه ویژگی‌ها و کاربردهای هر توزیع، روان و ساده مطرح و بررسی می‌کنیم.

توزیع نرمال (توزیع گاوسی)

توزیع نرمال که با نام توزیع گاوسی یا منحنی زنگی نیز شناخته می‌شود، یک توزیع پیوسته است که با منحنی زنگوله‌ای متقارن آن مشخص می‌شود. منحنی حول میانگین (µ) متمرکز است و با انحراف معیار آن (σ) تعریف می‌شود. در یک توزیع نرمال، میانگین، مد و میانه همه برابر هستند.

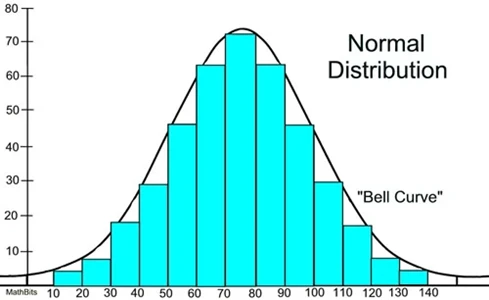
تقریباً 68٪ از مقادیر در ناحیه یک برابری انحراف معیار از میانگین، 95٪ در دو برابر انحراف معیار، و 99.7٪ در ناحیه سه  برابری انحراف معیار قرار می‌گیرند.

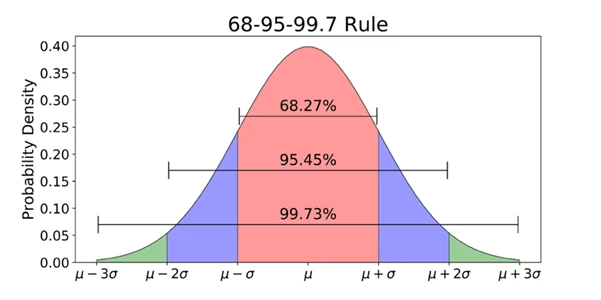
کاربردهای توزیع نرمال:

توزیع نرمال در بسیاری از پدیده‌های طبیعی و اجتماعی رواج دارد که آن را به ابزاری حیاتی در زمینه‌های مختلف تبدیل کرده است. برخی از کاربردهای آن عبارتند از:

• کمی‌سازی خطاهای اندازه‌گیری در آزمایش‌های علمی
• تجزیه و تحلیل نمرات آزمون یا سایر معیارهای کارایی
• مدل‌سازی بازده سهام در امور مالی
• ارزیابی کنترل فرآیند و تضمین کیفیت در تولید

پیاده سازی در پایتون:

from scipy.stats import norm
import matplotlib.pyplot as plt
import numpy as np
x1 = np.arange(-20, 20, 0.1)
y1 = norm.pdf(x1, 0, 5)
y2 = norm.pdf(x1, 0, 3)
y3 = norm.pdf(x1, 5, 3)
plt.plot(x1, y2) 
plt.plot(x1, y1)
plt.plot(x1, y3) 
plt.legend(["Standard deviation 3", "Standard deviation 5", "mean value of 5"], loc="upper left

تصویر خروجی:

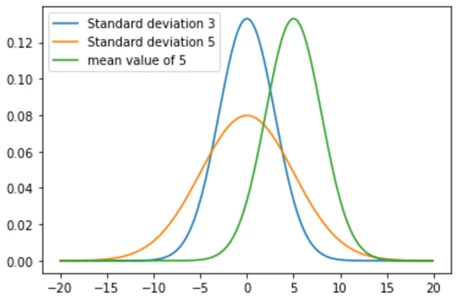
توزیع لاگ - نرمال (log-normal)

توزیع لاگ نرمال یک توزیع احتمال پیوسته از یک متغیر تصادفی است که لگاریتم آن به طور نرمال توزیع شده است. بنابراین، اگر متغیر تصادفی X به صورت log-normal توزیع شده باشد، Y = ln(X) دارای توزیع نرمال است. یک متغیر تصادفی که به طور لاگ نرمالی توزیع شده است فقط مقادیر مثبت را می‌گیرد. در نتیجه، توزیع‌های لاگ نرمال منحنی‌هایی را ایجاد می‌کنند که دارای انحراف راست هستند.

کاربردهای توزیع لاگ نرمال:

• توزیع Log-normal در سناریوهای واقعی بسیار رایج است.
• اکثر متغیرهایی که حاوی مقادیر پولی هستند، معمولاً دارای توزیع لاگ نرمال هستند - برای مثال خرید مشتریان در یک فروشگاه.
• توزیع درآمد؛
• وزن بزرگسالان
• اغلب، پدیده هایی که شانسی برای داشتن مقادیر منفی ندارند و ممکن است مقادیر مثبت شدید داشته باشند می توانند با این توزیع مدل شوند.

پیاده‌سازی در پایتون:

from scipy.stats import lognorm
X = np.linspace(0, 6, 500)
std = 1
mean = 0
lognorm_distribution = lognorm([std], loc=mean)
lognorm_distribution_pdf = lognorm_distribution.pdf(X)
fig, ax = plt.subplots(figsize=(8, 5))
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=1")
ax.set_xticks(np.arange(min(X), max(X)))
std = 0.5
mean = 0
lognorm_distribution = lognorm([std], loc=mean)
lognorm_distribution_pdf = lognorm_distribution.pdf(X)
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=0.5")
std = 1.5
mean = 1
lognorm_distribution = lognorm([std], loc=mean)
lognorm_distribution_pdf = lognorm_distribution.pdf(X)
plt.plot(X, lognorm_distribution_pdf, label="μ=1, σ=1.5")

تصویر خروجی:

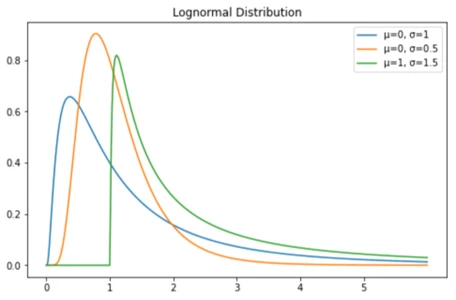
به عنوان مثال دیگر، از numpy برای تولید این توزیع log-normal استفاده می کنیم:

import seaborn as sns
np.random.seed(42)
sns.kdeplot(np.random.lognormal(mean = 3, sigma = 1, size = 1000)).set(title='Density Plot of Log Normal Distribution')
plt.xlim([0,500])

با تصویر خروجی:

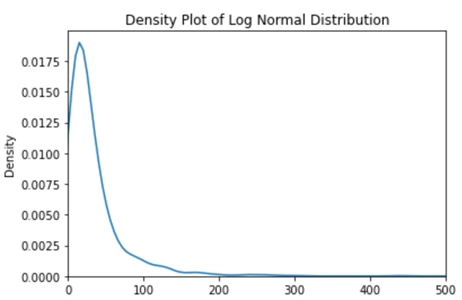
حال، اگر با استفاده از np.log یک لگاریتم روی داده‌های تولید شده اعمال کنیم، اتفاق جالبی رخ می دهد:

np.random.seed(42)
sns.kdeplot(np.log(np.random.lognormal(mean = 3, sigma = 1, size = 1000))).set(title='Density Plot of Transformed Log Normal Distribution')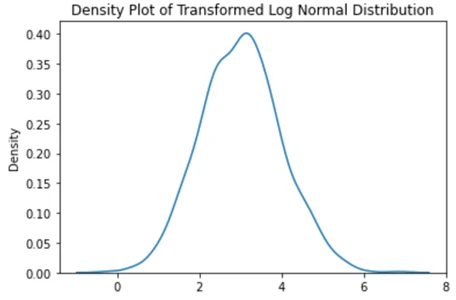

این نمودار را تشخیص می‌دهید؟ بله، در واقع یک توزیع نرمال است! 

توزیع یکنواخت

در آمار، توزیع یکنواخت به توزیع آماری اطلاق می شود که در آن همه نتایج به یک اندازه محتمل هستند. پرتاب یک تاس شش وجهی را در نظر بگیرید. احتمال یکسانی برای به دست آوردن هر شش عدد در پرتاب بعدی خود دارید، یعنی احتمال اینکه دقیقاً یکی از 1، 2، 3، 4، 5 یا 6 را به دست آورید، برابر با احتمال ۶/۱ است. از این رو نمونه‌ای از توزیع یکنواخت گسسته است. نمودار توزیع یکنواخت حاوی میله‌هایی با ارتفاع مساوی است که هر نتیجه را نشان می‌دهد که در این مثال ۶/۱ (0.166667) است.

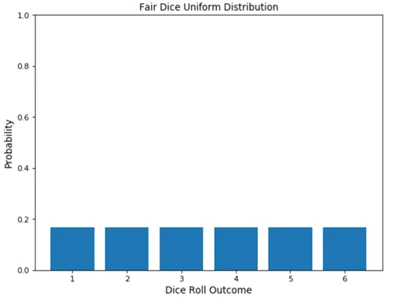
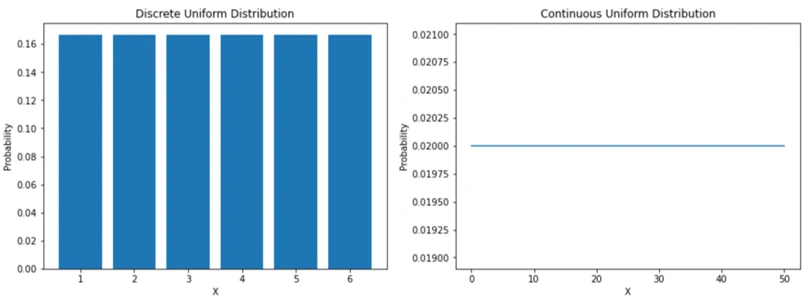
مشابه توزیع یکنواخت گسسته، توزیع یکنواخت پیوسته برای متغیرهای پیوسته وجود دارد. در توزیع یکنواخت پیوسته، همه مقادیر در یک محدوده مشخص، احتمال وقوع یکسانی دارند. این توزیع با مقادیر حداقل (a) و حداکثر (b) که محدوده را مشخص می کنند، بیان می‌شود. تابع چگالی احتمال ثابت است و برابر است با

 /(b-a)۱.

مشکل این توزیع این است که اغلب اطلاعات مرتبطی را در اختیار ما قرار نمی‌دهد. برای مثال پرتاب تاس، امید ریاضی 3.5 است، که شهود دقیقی به ما نمی‌دهد زیرا از آنجایی که همه مقادیر به یک اندازه محتمل هستند، هیچ قدرت پیش بینی واقعی به ما نمی‌دهد.

کاربردهای توزیع یکنواخت:

توزیع یکنواخت اغلب در سناریوها بدون دانش قبلی یا هنگامی که دلیلی برای برتری یک نتیجه بر نتیجه دیگر وجود ندارد، استفاده می‌شود. برخی از کاربردهای آن عبارتند از:

• شبیه‌سازی رویدادهای تصادفی در برنامه‌ها یا بازی‌های کامپیوتری
• تخصیص منابع به طور مساوی بین گزینه‌های مختلف
• مدل‌سازی احتمال مساوی کشیدن یک کارت خاص از یک دسته کارت به خوبی در هم ریخته شده

پیاده‌سازی در پایتون:

import numpy as np 
import matplotlib.pyplot as plt
from scipy import stats
# for continuous 
a = 0
b = 50
size = 5000
X_continuous = np.linspace(a, b, size)
continuous_uniform = stats.uniform(loc=a, scale=b)
continuous_uniform_pdf = continuous_uniform.pdf(X_continuous)
# for discrete
X_discrete = np.arange(1, 7)
discrete_uniform = stats.randint(1, 7)
discrete_uniform_pmf = discrete_uniform.pmf(X_discrete) 
# plot both tables
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(15,5))
# discrete plot
ax[0].bar(X_discrete, discrete_uniform_pmf)
ax[0].set_xlabel("X")
ax[0].set_ylabel("Probability")
ax[0].set_title("Discrete Uniform Distribution")
# continuous plot
ax[1].plot(X_continuous, continuous_uniform_pdf)
ax[1].set_xlabel("X")
ax[1].set_ylabel("Probability")
ax[1].set_title("Continuous Uniform Distribution")

تصویر خروجی:

توزیع برنولی

توزیع برنولی یکی از ساده‌ترین توزیع‌ها است که می‌توان از آن به عنوان نقطه شروع برای استخراج توزیع‌های پیچیده‌تر استفاده کرد. هر رویدادی با یک آزمایش و تنها دو نتیجه، از توزیع برنولی پیروی می‌کند. پرتاب سکه یا انتخاب بین درست و نادرست در آزمون، نمونه‌هایی از توزیع برنولی هستند. بنابراین، توزیع برنولی یک توزیع احتمال گسسته است که  دارای مقدار 1 با احتمال p و 0 با احتمال 1-p است. امید ریاضی توزیع برنولی به صورت E(x) = p و واریانس به صورت Var(x) = p(1-p)محاسبه می‌شود. 

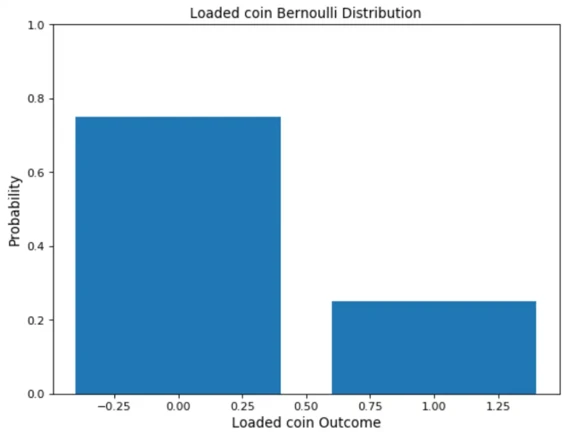
درک نمودار توزیع برنولی ساده است زیرا فقط از دو میله تشکیل شده است که یکی به احتمال p و دیگری به 1-pاست.

پیاده‌سازی در پایتون:

from scipy.stats import bernoulli
import matplotlib.pyplot as plt
# Specified probability parameter
p = 0.5
x = [i for i in range(0,10)]
# Sample according to Bernoulli distribution
y = bernoulli.rvs(p, size=10)
plt.hist(y)

اگر چه توزیع برنولی یکی از ساده‌ترین توزیع‌ها است اما سادگی را نباید با اهمیت اشتباه گرفت. در واقع، مدل‌سازی مقدار p توزیع برنولی ممکن است کار بسیار سختی باشد. بیایید تصور کنیم که یک کارآزمایی تصادفی با 100 بیمار انجام شده است و یک داروی خاص به آنها داده شده است. نتیجه آن می تواند درمان (1) یا عدم درمان (0) باشد. هر یک از نتایج فقط یک بار اتفاق می‌افتد و هیچ‌کس نمی تواند دو بار درمان شود. متأسفانه 70 نفر از بیماران درمان نشدند و فقط 30 نفر درمان شدند. اکنون می‌توان احتمال موفقیت را استخراج کرد: (30+70)30/یعنی p=30. شبیه‌سازی آن در پایتون به صورت زیر است:

import seaborn as sns
import numpy as np
bernoulli = np.array([0]*70+[1]*30)
sns.histplot(bernoulli, stat='probability').set_title('Bernoulli Trials')

توزیع برنولی از یک p منحصربفرد (30٪) تشکیل شده است و تخمین این مقدار p در سناریوهای زندگی واقعی واقعاً سخت است . به عنوان مثال، در بالا فرض شد که 30٪ احتمال درمان با دارو است، اما این عدد ممکن است به طور تصادفی اتفاق افتاده باشد. در شرایط زندگی واقعی، معمولاً چنین است که تخمینی از مقدار واقعی p  برای کل جمعیت فرض می‌شود. درک آزمایش برنولی برای پرتاب سکه آسانتر است زیرا این مقادیر قطعی هستند (50٪ شانس برای شیر در مقابل خط)

کاربردهای توزیع برنولی:

• احتمال موفقیت یک جراحی؛
• احتمال عدم پرداخت بدهی مشتری در 90 روز اول وام.
• احتمال اینکه مشتری روی یک تبلیغ خاص کلیک کند.

توزیع دو جمله‌ای

توزیع دو جمله‌ای تعمیم توزیع برنولی است. در واقع، توزیع دوجمله‌ای یک توزیع گسسته است که تعداد موفقیت‌ها را در تعداد ثابتی از آزمایش‌های برنولی (آزمایش‌های مستقل با دو نتیجه ممکن: موفقیت یا شکست) مدل می‌کند. در توزیع برنولی، سکه را یک بار پرتاب می‌کنیم، اما توزیع دوجمله‌ای را می‌توان به‌ عنوانn  بار آزمایش‌ پرتاب با احتمال p شیر بودن و 1-p  خط بودن در هر بار در نظر گرفت. توزیع با تعداد آزمایشات (n) و احتمال موفقیت (p) در هر آزمایش مشخص می‌شود.

به عنوان مثال، فرض کنید که یک شرکت شیرینی‌سازی هم شکلات شیری و هم شکلات تیره تولید می‌کند. کل محصولات شامل نیمی از تکه‌های شکلات شیری و نیمی شکلات تیره است. فرض کنید ده شکلات را به صورت تصادفی انتخاب کرده‌اید و انتخاب شکلات شیری به عنوان یک موفقیت تعریف شده است. توزیع احتمال تعداد موفقیت‌ها در طول این ده آزمایش با p = 0.5 در نمودار توزیع دو جمله‌ای نشان داده شده است:

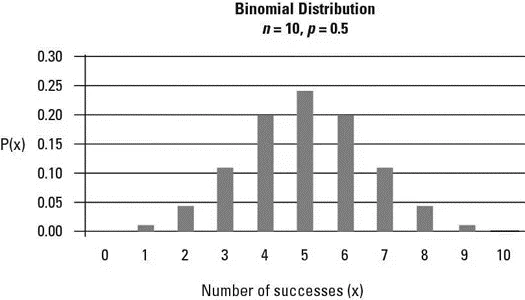
کاربردهای توزیع دو جمله‌ای:

توزیع دو جمله‌ای معمولاً زمانی استفاده می‌شود که احتمال موفقیت در طول آزمایش‌ها ثابت بماند. برخی از کاربردها عبارتند از:

• تجزیه و تحلیل تعداد شیرها در یک سری از پرتاب سکه
• تخمین تعداد اقلام معیوب در یک دسته تولید
• مدل‌سازی تعداد پاسخ‌های صحیح در آزمون چند گزینه‌ای

پیاده‌سازی در پایتون:

from scipy.stats import binom
import matplotlib.pyplot as plt
# Specified probability parameter
p = 0.5
n = 10
x = [i for i in range(0,n)]
# Sample according to Binomail distribution
y = binom.rvs(n, p, size=10)
plt.plot(x,y, "ob")

تصویر خروجی:

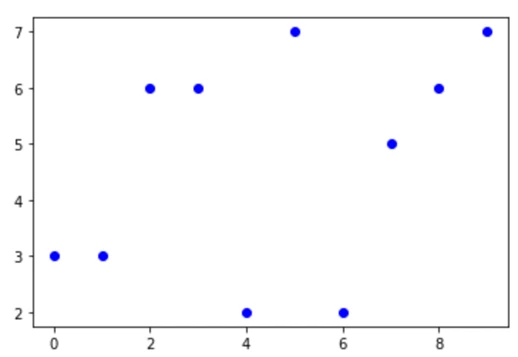
توزیع پواسون

توزیع پواسون بر اساس نام یک ریاضیدان فرانسوی به نام سیمئون دنیس پواسون نامگذاری شده است. توزیع پواسون یک توزیع گسسته است که تعداد رویدادهای رخ داده در یک بازه زمانی یا مکانی ثابت را با توجه به میانگین نرخ وقوع ثابت (λ) مدل می‌کند. این توزیع با تک پارامتر آن، λ  مشخص می‌شود که نشان‌دهنده میانگین تعداد رویدادها در بازه زمانی است. در فرآیندهای پواسون، رویدادها مستقل از یکدیگرند و یک رویداد می‌تواند هر تعداد بار (در مدت زمان تعیین شده) رخ دهد و همچنین دو رویداد نمی‌توانند به طور همزمان اتفاق بیفتند.

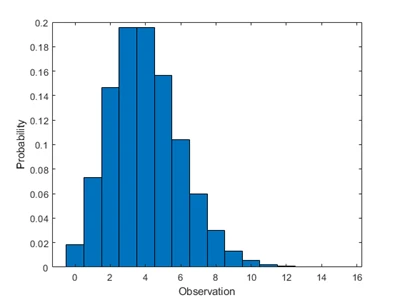
نمودار توزیع پواسون تعداد نمونه‌هایی را که یک رویداد در بازه زمانی استاندارد رخ می دهد و احتمال هر یک را ترسیم می‌کند.

کاربردهای توزیع پواسون:

توزیع پواسون به طور گسترده برای مدل‌سازی رویدادها یا رخدادهای نادر در زمینه‌های مختلف استفاده می‌شود. برخی از کاربردهای آن عبارتند از:

• تخمین تعداد تماس‌های تلفنی دریافت شده در یک مرکز تماس در ساعت
• مدل‌سازی تعداد محصولات معیوب در یک محصول تولیدی
• تجزیه و تحلیل تعداد تصادفات در یک تقاطع در یک دوره معین

پیاده‌سازی در پایتون:

from scipy.stats import binom
import matplotlib.pyplot as plt
# Specified probability parameter
p = 0.5
n = 10
x = [i for i in range(0,n)]
# Sample according to Binomail distribution
y = binom.rvs(n, p, size=10)
plt.plot(x,y, "ob")

با خروجی زیر:

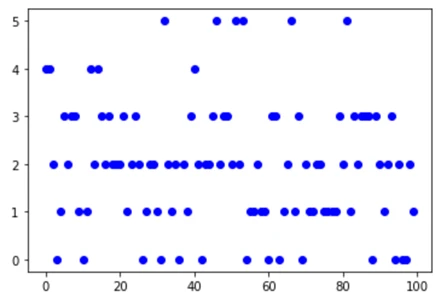
کد بالا شبیه‌سازی می‌کند که اگر میانگین، 2 رویداد در واحد زمان باشد، چند رویداد خواهید داشت. نتیجه به شرح زیر است: می توانید ببینید که شدت در مقادیر پایین‌تر متمرکز شده است، اما گاهی اوقات، مقادیر بالاتری دریافت می‌کنید. می‌توان این را در زندگی روزمره نیز اعمال کرد! اگرچه به طور متوسط، ما اتفاقات خوب زیادی را در یک روز نخواهیم دید، اما زمان‌هایی در زندگی خود خواهیم داشت که اتفاقات خوب زیادی در یک روز رخ می دهد. 

به عنوان مثال دیگر، بیایید یک تیم فوتبال به نام "A-Team" را در نظر بگیریم.  این تیم در 10 بازی گذشته ۲۵ گل به ثمر رسانده است. می‌توان از یک میانگین ساده برای تخمین میانگین تعداد گل‌های زده شده توسط این تیم استفاده کرد که 2.5 گل بدست می‌آید. بنابراین، با فرض اینکه به طور میانگین 2.5 گل به ثمر رسیده است، توزیع مورد انتظار گل‌های "A-Team"  در 100 بازی بعدی چگونه خواهد بود؟

sns.histplot(np.random.poisson(lam = 2.5, size = 100)).set(title='Histogram of Poisson Distribution of 100 games with lambda=2.5')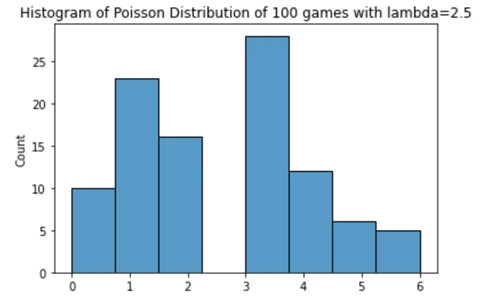

با این داده‌ها، اکنون می‌توانیم احتمال اینکه این تیم می‌تواند چه تعداد گل برای بازی‌های بعدی به ثمر برساند، را تجسم کنیم. تقریباً می توانیم ببینیم که این تیم:

• 33٪  شانس به ثمر رساندن 0 یا 1 گل در بازی بعدی دارد.
• 27٪شانس دارد که دقیقاً 2 گل در بازی بعدی به ثمر برساند.
• 40%  شانس به ثمر رساندن بیش از 2 گل در بازی دارد.

یک نکته کوچک در این مثال وجود دارد. برای اینکه فرآیندی با استفاده از توزیع پواسون مدل شود، رویدادها باید مستقل باشند. این چیزی است که برای یک تیم فوتبال صدق نمی‌کند زیرا یک بازی می‌تواند بر روحیه بازیکن‌ها در بازی بعدی و روی اهداف مورد انتظار تأثیر بگذارد. با این وجود، چندین بار آزمایش شده است که گل‌هایی که تیم‌های فوتبال به ثمر می‌رسانند، در طول یک فصل از توزیع پواسون پیروی می‌کنند.

توزیع نمایی

توزیع نمایی یکی از توزیع‌های پیوسته پرکاربرد است. برای مدل‌سازی زمان بین رویدادهای مختلف در فرآیند پواسون استفاده می‌شود (جایی که رویدادها به طور مستقل و با نرخ میانگین ثابت رخ می‌دهند). به عنوان مثال، در فیزیک، اغلب برای اندازه‌گیری واپاشی رادیواکتیو، در مهندسی، برای اندازه‌گیری زمان مربوط به دریافت یک قطعه معیوب در خط مونتاژ و در امور مالی، برای اندازه گیری احتمال عدم موفقیت بعدی برای پرتفوی دارایی‌های مالی استفاده می‌شود. یکی دیگر از کاربردهای رایج توزیع‌های نمایی در تجزیه و تحلیل بقا است برای مثال، عمر مورد انتظار یک دستگاه/ماشین. این توزیع با پارامتر واحد آن، λ، مشخص می‌شود که میانگین نرخ وقوع را نشان می‌دهد.

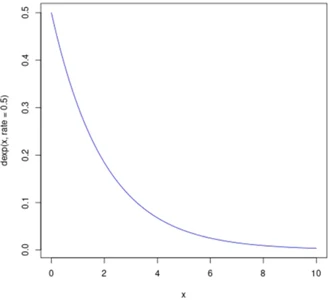
نمودار نمایی یک خط منحنی است که نشان دهنده چگونگی تغییر احتمال به صورت نمایی است. 

کاربردهای توزیع نمایی:

توزیع‌های نمایی معمولاً در محاسبات قابلیت اطمینان محصول یا مدت زمان ماندگاری محصول یا برای مدل‌سازی زمان‌های انتظار یا سناریوهای زمان موردنیاز تا شکست استفاده می‌شوند. برخی از کاربردهای آن عبارتند از:

• تجزیه و تحلیل زمان بین ورود مشتری به فروشگاه یا مرکز خدمات
• تخمین زمان تا خرابی یک قطعه یا ماشین الکترونیکی
• مدل سازی زمان بین بلایای طبیعی یا سایر رویدادهای نادر

پیاده‌سازی در پایتون:

from scipy.stats import expon
import matplotlib.pyplot as plt
# Specified probability parameter
mu = 2
n = 100
x = [i for i in range(0,n)]
# Sample according to exponential distribution
y = expon.rvs(scale=2, size=n)
plt.plot(x,y, "ob")

با خروجی زیر:

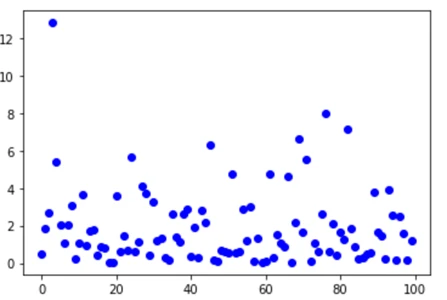
توزیع هندسی

توزیع هندسی یک توزیع گسسته است که تعداد آزمایش‌های برنولی مورد نیاز برای دستیابی به اولین موفقیت را مدل می‌کند. توزیع با تنها پارامتر آن، p، مشخص می شود که احتمال موفقیت در هر آزمایش را نشان می‌دهد. تابع جرم احتمال توزیع هندسی با P(X=k) = p(1-p)^(k-1) به دست می‌آید که در آن k تعداد آزمایشات است.

کاربردهای توزیع هندسی:

توزیع هندسی در سناریوهایی مفید است که ما به تعداد آزمایش‌ها تا رسیدن به اولین موفقیت علاقه مندیم. برخی از کاربردهای آن عبارتند از:

• تعیین تعداد پرتاب سکه تا زمانی که اولین شیر ظاهر شود
• تخمین تعداد تماس‌هایی که یک فروشنده باید قبل از فروش انجام دهد
• تجزیه و تحلیل تعداد تلاش‌های لازم برای قبولی در آزمون رانندگی

پیاده‌سازی در پایتون:

from scipy.stats import geom 
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 5, 100)
# Varying positional arguments
a, b = 0.2, 0.8
y = geom.ppf(x, a, b)
plt.plot(x, y)

با خروجی زیر:

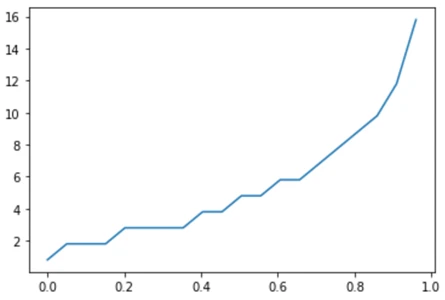
توزیع بتا

توزیع بتا یک توزیع پیوسته است که در بازه [0،1]  تعریف شده است، که آن را به ویژه برای مدل‌سازی احتمالات یا نسبت‌ها مفید می‌کند.توزیع با دو پارامتر ، α  و β مشخص می‌شود که درست مانند میانگین و انحراف معیار در توزیع گاوسی، شکل توزیع را کنترل می‌کنند که با حجم نمونه و میانگین مرتبط هستند. توزیع بتا اغلب در استنتاج بیزی به عنوان توزیع prior استفاده می‌شود که در این جا نمی‌توان جزئیات آن را در چند جمله توضیح داد. توزیع بتا بسیار انعطاف‌پذیر است و بسته به مقادیر α و β شکل های مختلفی می‌تواند به خود بگیرد.

کاربردهای توزیع بتا:

توزیع بتا به طور گسترده در آمار بیزی استفاده می‌شود، زیرا می‌تواند به عنوان توزیع قبلی برای توابع احتمال مختلف عمل کند. برخی از کاربردهای آن عبارتند از:

• مدل‌سازی احتمال موفقیت در یک آزمایش دو جمله‌ای زمانی که اطلاعات قبلی در دسترس باشد
• تخمین نسبت اقلام معیوب در یک فرآیند تولید
• تجزیه و تحلیل نرخ تبدیل کمپین های بازاریابی آنلاین

پیاده‌سازی در پایتون:

from scipy.stats import beta
import matplotlib.pyplot as plt
# Specified probability parameter
a = 2
b = 3
n = 100
x = [i for i in range(0,n)]
# Sample according to Beta distribution
y = beta.rvs(a, b, size=n)
plt.plot(x,y, "ob")

یک نمونه قرعه کشی تصادفی بر اساس توزیع بتا به شکل زیر خواهد بود:

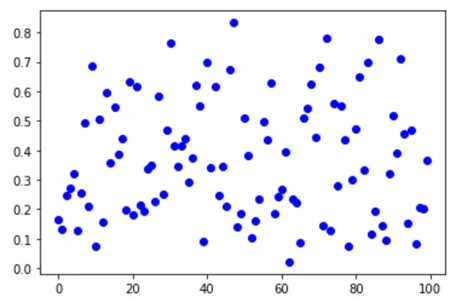
به عنوان مثال دیگر، بیایید فرض کنیم یک سکه biased را 50 بار پرتاب کنیم که  30 بار روی شیر و 20 بار روی خط می‌افتد. در این حالت 30 موفقیت و 20 شکست داریم و نمودار توزیع بتا به شرح زیر است:

# Import packages
from scipy.stats import beta 
import matplotlib.pyplot as plt
import numpy as np
# Plot the distribution
alpha = 31
beta1 = 21
x = np.arange (0, 1, 0.01)
y = beta.pdf(x, alpha, beta1)
plt.figure(figsize=(11,6))
plt.plot(x, y, linewidth=3)
plt.xlabel('x', fontsize=20)
plt.ylabel('PDF', fontsize=20)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.axvline(0.6, linestyle = 'dashed', color='black')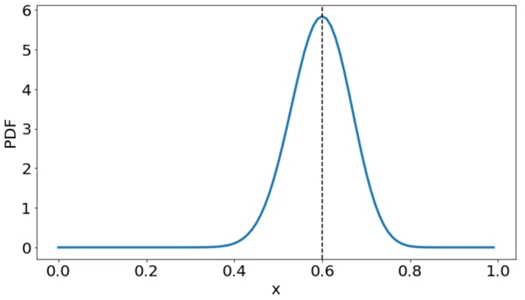

می بینیم که محتمل‌ترین احتمال فرود این سکه روی شیرها 0.6 است (30/50 = 0.6). علاوه بر این، توجه داشته باشید که قبل از 0.4 و بعد از 0.8، احتمال اینکه سکه این مقادیر را به دست آورد تقریباً 0 است.

توزیع گاما

مانند توزیع بتا، توزیع گاما نیز توزیع احتمال پیوسته دو پارامتری است که زمان انتظار را تا زمانی که تعداد دلخواه رویداد در فرآیند پواسون رخ دهد، مدل می‌کند. برخی از شکل‌های خاص توزیع گاما شامل توزیع نمایی ذکر شده در بالا و توزیع Chi-square است که بعداً مورد بحث قرار خواهد گرفت. این توزیع با پارامتر شکل (k) و پارامتر مقیاس (θ) مشخص می‌شود. هنگامی که پارامتر شکل برابر با 1 باشد، توزیع گاما به توزیع نمایی کاهش می‌یابد.

کاربردهای توزیع گاما:

توزیع گاما در زمینه‌های مختلف برای مدل‌سازی زمان انتظار، طول عمر یا سایر متغیرهای پیوسته و غیر منفی استفاده می‌شود. برخی از کاربردهای آن عبارتند از:

• تخمین زمان تا خرابی یک سیستم پیچیده با اجزای متعدد
• مدل‌سازی زمان انتظار تا رسیدن تعداد مشخصی از مشتریان به مرکز خدمات
• تجزیه و تحلیل طول عمر یک جمعیت بیولوژیکی یا طول مدت بیماری‌های خاص

پیاده‌سازی در پایتون:

from scipy.stats import gamma
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import gamma
a = 100 #scale parameter (alpha)
x = np.linspace(gamma.ppf(0.01, a),
                gamma.ppf(0.99, a), 100)
plt.plot(x, gamma.pdf(x, a),lw=5, alpha=0.6, label='gamma pdf')

با خروجی زیر:

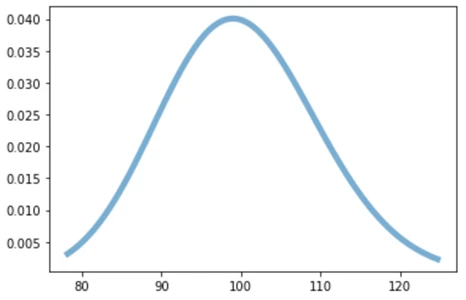
می بینید که توزیع گاما الگوی متفاوتی با توزیع بتا دارد.

توزیع توان دوم کای 

توزیع Chi-squared یکی از مهمترین و شناخته‌شده‌ترین توزیع‌ها برای دانشمندان داده و آماردانان است. این یک توزیع احتمال پیوسته در )بی نهایت[0, است و همچنین یک نمونه خاص از توزیع گاما است. پارامتری که می‌گیرد درجه آزادی نامیده می‌شود و طبق معمول این پارامتر، شکل توزیع را تعیین می‌کند. این توزیع احتمال محبوب معمولاً در آزمون فرض و در ساخت فواصل اطمینان استفاده می‌شود.

پیاده‌سازی در پایتون:

from scipy.stats import chi2
import matplotlib.pyplot as plt
# Specified probability parameter
df1 = 10
df2 = 20
df3 = 30
df4 = 40
df4 = 40
df5 = 50
# calculate range we want to display
x = np.linspace(0,30, 500)
# Sample according to chi2 distribution
rv1 = chi2(df1)
rv2 = chi2(df2)
rv3 = chi2(df3)
rv4 = chi2(df4)
rv5 = chi2(df5)
plt.plot(x, rv1.pdf(x), 'r', label='df = 10')
plt.plot(x, rv2.pdf(x), 'g',label='df = 20')
plt.plot(x, rv3.pdf(x), 'b', label='df = 30')
plt.plot(x, rv4.pdf(x), 'black',label='df = 40')
plt.plot(x, rv5.pdf(x), 'yellow',label='df = 50')
plt.legend(loc="upper left")

با خروجی زیر:

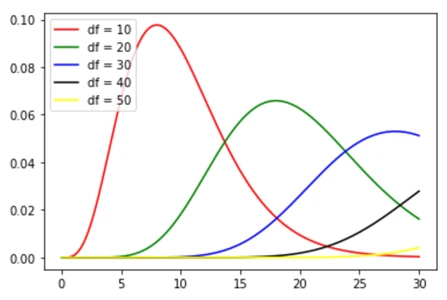
یکی دیگر از مواردی که اغلب توسط دانشمندان داده استفاده می‌شود، آزمون Chi-square است که به طور ویژه برای محاسبه برازش داده‌های نمونه با توجه به توزیع پیشنهادی یا آزمون استقلال استفاده می‌شود. در scipy.stats، به راحتی می‌توان آمار آزمون Chi-squared را توسط scipy.stats.chisquare (your_sample, expected_distribution)  محاسبه کرد. استفاده از آن فوق العاده آسان است!

توزیع تی (دانشجویی)

توزیع t-student، که همچنین به عنوان توزیع t شناخته می‌شود، یک نوع توزیع آماری شبیه به توزیع نرمال با شکل زنگی است، اما دنباله‌های سنگین‌تری دارد. تفاوت مهم دیگر بین توزیع t و توزیع نرمال این است که غیر از میانگین و واریانس، باید درجات آزادی (Degree of freedom) برای توزیع تعریف شود (مانند توزیع  Chi-square). DoF  شکل توزیع را کنترل می‌کند. در آمار، تعداد درجات آزادی، تعداد مقادیری است که در محاسبه نهایی یک آماره وجود دارند. 

زمانی که حجم نمونه کوچک است، از توزیع t به جای توزیع نرمال استفاده می‌شود. برای مثال، فرض کنید با کل سیب فروخته شده توسط یک مغازه‌دار در یک ماه سروکار داریم. در این صورت از توزیع نرمال استفاده خواهیم کرد. حال اگر با مقدار کل سیب فروخته شده در یک روز سروکار داشته باشیم، یعنی نمونه کوچکتر، می توانیم از توزیع t استفاده کنیم.

توزیع t به صورت t(k) نشان داده می شود، که در آن k نشان دهنده تعداد درجات آزادی است. برای k=2، یعنی 2 درجه آزادی و امید ریاضی برابر با میانگین است. توزیع t-student نقش مهمی در انجام آزمون فرض با داده های محدود دارد.

پیاده‌سازی در پایتون:

from scipy.stats import t
from scipy.stats import norm
import matplotlib.pyplot as plt
# Specified probability parameter
df1 = 1
df2 = 2
df3 = 3
df4 = 4
# calculate range we want to display
x = np.linspace(-10,
10, 200)
# Sample according to t distribution
rv1 = t(df1)
rv2 = t(df2)
rv3 = t(df3)
rv4 = t(df4)
plt.plot(x, rv1.pdf(x), 'r', label='df = 10')
plt.plot(x, rv2.pdf(x), 'g',label='df = 20')
plt.plot(x, rv3.pdf(x), 'b', label='df = 30')
plt.plot(x, rv4.pdf(x), 'black',label='df = 40')
plt.plot(x, norm.pdf(x), 'yellow', label='Gaussian')
plt.legend(loc="upper left")

با خروجی زیر:

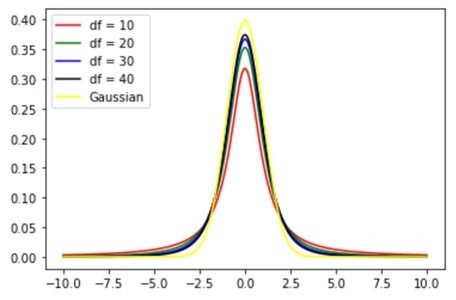
عمداً توزیع گاوسی را در تصویر قرار داده شده است تا بتوانید دید واضحی از تفاوت آنها داشته باشید. می‌توان دید که توزیع گاوسی دارای دنباله‌های کوچکتر از توزیع t و همچنین قله‌های بزرگتر است.

مانند آنچه در توزیع Chi-square گفته شد، می توان آزمون t را با استفاده از پایتون نیز انجام داد. در قطعه کد زیر، یک آزمون t  انجام شده است تا آزمایش شود که آیا نمونه از دو توزیع متفاوت است یا خیر.

from scipy import stats
seed = np.random.default_rng()
# Ground truth: sampling from same distribution
rvs1 = stats.norm.rvs(loc=5, scale=10, size=500, random_state=seed)
rvs2 = stats.norm.rvs(loc=5, scale=10, size=500, random_state=seed)
print(stats.ttest_ind(rvs1, rvs2))
# Sample response, it varies a lot
# Cannot say any thing definite from result given p value
# Ttest_indResult(statistic=-0.7362272777889193, pvalue=0.46176540317360304)
rvs3 = stats.norm.rvs(loc=0, scale=10, size=500, random_state=seed)
print(stats.ttest_ind(rvs1, rvs3))
# Sample response, it varies a lot
# We can say with a lot of confidence two data are not from same distribution
# Ttest_indResult(statistic=8.065543453125999, pvalue=2.078369795336982e-15)

با توجه به کامنت‌ها می‌توانید متوجه شوید که آزمون  tبسیار دقیق است. (در اینجا، p-value می‌تواند اطمینان آزمون را تعیین کند یعنی آزمون t مشخص می‌کند که rvs1 و rvs2 از یک مکان نیستند که این با حقیقت مطابقت دارد.)

با درک این توزیع‌های رایج داده‌ها و ویژگی‌های آن‌ها، برای شناسایی توزیع مناسب برای داده‌های خود و استفاده از تکنیک‌های آماری صحیح برای تجزیه و تحلیل و تفسیر داده‌ها، مجهزتر خواهید بود.