آموزش طراحی الگورتیمی با استفاده از Dot Product و Cosine Similarity جهت یافتن مقالات مرتبط در وب‌سایت

همواره یکی از دغدغه‌های وب‌مسترها و صاحبین کسب‌وکارهای آنلاین این است که با ارائهٔ محتواهای مرتبط با یک مقاله، محصول و غیره، از یکسو تجربه‌ٔ کاربری بهتری برای کاربران خود رقم بزنند و از سوی دیگر درآمدزایی خود را با ماندگاری بیشتر کاربران در سایت ارتقاء بخشند که در همین راستا در این مقاله قصد داریم طراحی الگوریتمی را مورد بررسی قرار دهیم که چنانچه درست پیاده‌سازی گردد، می‌تواند به‌ سادگی محتواهای مرتبط را یافته و در معرض دید کاربران قرار دهد.

در سیستم‌های مدیریت محتوایی همچون وردپرس و غیره، محتوای یک سایت در چندین Category (دسته‌بندی) مختلف قرار می‌گیرد و بدین شکل محتوای سایت طبقه‌بندی می‌گردد اما استفاده از این نوع دسته‌بندی چندین نقطه ضعف عمد دارد؛ اول اینکه در طول زمان ممکن است به این نتیجه برسیم که یک دسته‌بندی بایستی حذف گردد و یا پس از مدتی بخواهیم یک دسته‌ را با دستهٔ دیگری ادغام کنیم و مشکلاتی از این دست.

آنچه امروزه بیشتر دیده می‌شود، استفاده از Tag (تگ یا برچسب) برای دسته‌بندی محتوای مختلف است. به‌ عبارت دیگر، با استفاده از تگ‌ها می‌توانیم با یک تیر دو نشان بزنیم به طوری که هم دسته‌بندی محتواها را مشخص ساخته و هم ارتباط یک محتوا را با دیگر محتواها یافته و به‌ عنوان محتوای مرتبط در معرض دید کاربران قرار دهیم.

یکی از راه‌کارهایی که در عمل ساده‌ترین کار اما در عین‌ حال نامؤثرترین راه می‌باشد این است که اولین تگ در نظر گرفته شده برای محتوایی خاص را گرفته و دیگر محتواهایی که دارای آن تگ هستند را از دیتابیس فراخوانی کنیم و به‌ عنوان محتوای مرتبط به کاربر نشان دهیم اما این در حالی است که این روش اصلاً اثربخش نبوده و ضریب خطای بالایی دارد که برای روشن‌تر شدن این مسأله، مثالی از وبلاگ سکان آکادمی می‌زنیم.

یکی از مقالات وبلاگ تحت‌ عنوان MicroPython: نسخهٔ کاستومایز شده‌ای از زبان برنامه‌نویسی پایتون برای دیوایس‌های اِمبدد که دارای تگ‌های برنامه‌نویسی، اپن‌سورس، میکروپایتون و پایتون است را مد نظر قرار می‌دهیم. همان‌طور که مشخص است، اولین تگ این مقاله برنامه‌نویسی است و در صورتی‌ که بخواهیم دیگر محتواهای مرتبط با این مقاله را از دیتابیس فراخوانی کنیم، یک کوئری می‌زنیم به دیتابیس با این مضمون که هر آنچه محتوا با تگ برنامه‌نویسی است را بیابد و در معرض دید کاربران قرار دهد که در چنین شرایطی، مقاله زیر به‌ طور حتم جزو پیشنهادات چنین الگوریتمی غیربهینه‌ای خواهد بود:

- Toilet Testing: راه‌کارهای آموزشی گوگل جهت تست نرم‌افزار در سرویس‌ بهداشتی!

گرچه هر سه مقاله به‌ نوعی مرتبط با برچسب برنامه‌نویسی‌ هستند، اما اگر بخواهیم ریزبینانه نگاه کنیم، در مقالات پیشنهادی هیچ رنگ‌ و بویی از تگ‌های دیگر مقاله همچون اپن‌سورس یا پایتون دیده نمی‌شود و کاربری که این مقاله را می‌خواند به احتمال زیاد انتظار دارد تا دیگر مقالات پیشنهادی به‌ نوعی مرتبط با پایتون باشند.

استفادهٔ عملی از ریاضیات جهت یافتن محتواهای مرتبط
در الگوریتمی که قرار است طراحی کنیم، پیش از هر چیز می‌بایست با مفهومی تحت‌ عنوان K-nearest Neighbors Algorithm (الگوریتم نزدیک‌ترین همسایه) آشنا شویم. به‌ عبارت دیگر، برای هر پست می‌بایست نزدیک‌ترین تگ‌هایی که با محتوا سازگاری دارند را برگزید و این در حالی است که تگ‌ها نیز از شبیه‌ترین تگ به کم‌شباهت‌ترین تگ دارای رَنک (درجه‌بندی) می‌شوند که برای استفاده از این رویکرد، می‌بایست راهی بیابیم تا پست‌ها را بر اساس تگ‌هایشان با یکدیگر مقایسه کنیم که یکی از این‌ راه‌ها، نمایش بُرداری پست‌ها است که با استفاده از مفهومی تحت‌ عنوان Cosine Similarity (مشابهت کسینوسی) امکان‌پذیر است (مشابهت کسینوسی عبارت است از کسینوس زاویهٔ بین دو بردار.)

به‌ خاطر داشته باشیم دو پُستی که دقیقاً بُردارهایی به یک جهت داشته باشند (یعنی زاویهٔ هر دو بُردار برابر با صفر درجه باشد) دارای مشابهت کسینوسی یک هستند و این در حالی است که اگر بُردارهای دو پُست مختلف دارای جهات کاملاً متضاد با یکدیگر باشند (یعنی زاویهٔ هر دو بُردار ۹۰ درجه باشد)، دارای مشابهت کسینوسی صفر هستند (لازم به ذکر است پُست‌هایی که ۱۰۰٪ مشابه یکدیگر نباشند بین این دو عدد قرار می‌گیرند.) با این تفاسیر، می‌توانیم فرمولی برای یافتن میزان مشابهت هر دو پُست به صورت زیر در نظر بگیریم:

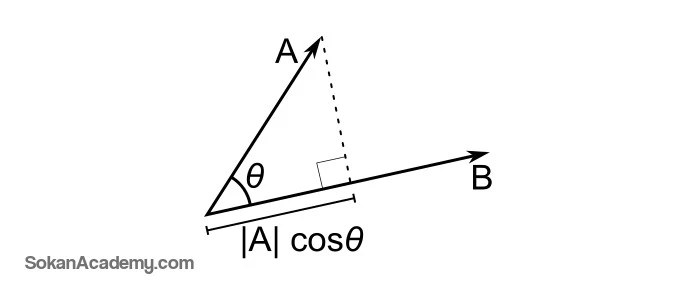
حال می‌بایست با استفاده از مفهومی تحت‌ عنوان Dot Product (ضرب داخلی)، به میزان مشابهت این دو بُردار پی‌ ببریم (ضرب داخلی یک عمل ریاضیاتی دوتایی مابین دو بُردار در فضایی با n بُعد است که نتیجهٔ آن یک عدد حقیقی است.) به‌ عبارت دیگر، با نمایش کلیهٔ پست‌ها به‌ عنوان ماتریسی با n ردیف که هر ردیف هم نشانگر بُردار یک پست است، می‌توان به‌ سادگی ضرب داخلی با پست مذکور انجام داده و برداری اِن‌بُعدی از میزان مشابهت پست مد نظر با سایر پست‌ها به‌ دست آورد (باز هم اگر بخواهیم ساده‌تر توضیح دهیم، می‌توان گفت که ضرب داخلی دو بُردار A و B در تصویر فوق برابر است با اندازهٔ تصویر بُردار A بر روی بُردار B که در تصویر فوق با نقطه‌چین مشخص شده است. در یک کلام، یعنی تعداد تگ‌های مشترک مابین دو پُست.)

برای روشن‌تر شدن این مسئله، مجدد به مثال مقالات فوق باز می‌گردیم. مقالهٔ «MicroPython: نسخهٔ کاستومایز شده‌ای از زبان برنامه‌نویسی پایتون برای دیوایس‌های اِمبدد» که از این پس آن‌ را تحت‌ عنوان بُردار A در نظر می‌گیریم دارای تگ‌های زیر است:

- برنامه‌نویسی
- اپن‌سورس
- میکروپایتون  
- پایتون

و مقاله‌ای همچون «EditorConfig: ابزاری به منظور مدیریت استایل سورس‌کد در ادیتورهای مختلف» که از این پس آن‌ را تحت‌ عنوان بُردار B در نظر می‌گیریم، دارای تگ‌های زیر است:

- برنامه‌نویسی
- ویرایشگر کد

با این تفاسیر، ضرب داخلی دو بُردار A و B می‌شود عدد ۱ زیرا فقط و فقط یک تگ (برنامه‌نویسی) مابین این دو بُردار مشترک است.

حال نیاز به فرمولی داریم تا درصد مشابهت این دو بُردار را در بیاوریم که فرمول زیر این‌ کار را برایمان انجام خواهد داد:

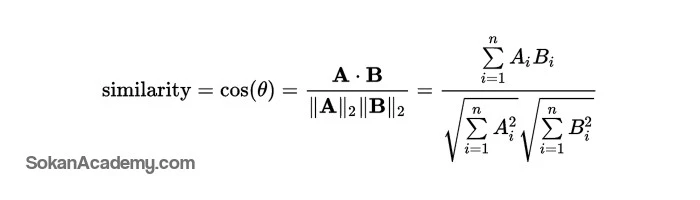
در تفسیر فرمول فوق، به‌ طور خلاصه بایستی بگوییم که میزان Similarity (مشابهت) برابر است با میزان ضرب داخلی بُردارهای A و B تقسیم بر اندازهٔ بُردار A ضرب در اندازهٔ بُردار B به طوری که در مثال فوق، اندازهٔ بُردار A برابر است با تعداد تگ‌های این مقاله که برابر با ۴ است و اندازهٔ بُردار B برابر است با تعداد تگ‌های مقالهٔ B که مساوی است با ۲ و در حقیقت اگر بخواهیم میزان مشابهت این دو مقاله را به‌ دست آوریم، عمل (2√ × 4√) ÷ 1 که تفسیر می‌شود به ضرب داخلی هر دو بُردار (یعنی عدد ۱) تقسیم‌ بر 4√ ضرب در 2√ که برابر است با 0.35355339059 به طوری که هرچه بُرداری دارای مقدار بزرگ‌تری باشد (مثلاً 0.99)، این بدان معنا است که میزان مشابهتش با پست مد نظرمان بیش از سایر پُست‌ها بوده و اگر برداری دارای مقدار 0 باشد هم حاکی از آن است که هر دو بُردار عمود بر یکدیگرند (زاویهٔ ۹۰ درجه که مقدار کسینوس در این زاویه برابر با ۰ است) و هیچ سِنخیتی با یکدیگر ندارند. در این مثال، میزان مشابهت هر دو مقاله چیزی در حدود ۳۵٪ است که به نوعی می‌توان گفت خیلی به هم ربطی ندارند.

تا اینجای بحث همه‌چیز تئوریک بود و ممکن است درک آن برای دولوپرهای تازه‌کار کمی مشکل باشد و در همین راستا در ادامه قصد داریم تا الگورتیم فوق را کدنویسی کرده تا ببینیم که در عمل خروجی چنین الگوریتمی چه خواهد بود.

پیاده‌سازی الگوریتم یافتن مقالات مرتبط در زبان PHP
پس از اینکه توانستیم الگوریتم مد نظر را روی کاغذ پیاده‌سازی کنیم، حال نوبت به کدنویسی آن می‌رسد که قصد داریم با زبان PHP این‌ کار را انجام دهیم (جهت شروع یادگیری این زبان، می‌توانید به دورهٔ آموزش PHP در سکان آکادمی مراجعه نمایید.) در ابتدا، تابعی تحت‌ عنوان ()calSimilarity به‌صورت زیر می‌نویسیم:

function calSimilarity($firstContent, $secondContent) { 
    $dotProduct = count(array_intersect($firstContent['tags'], $secondContent['tags'])); 
    $cosineSimilarity = $dotProduct / (sqrt(count($firstContent['tags'])) * sqrt(count($secondContent['tags']))); 
    return $cosineSimilarity; 
}

تابع فوق دو پارامتر ورودی تحت‌ عناوین firstContent$ و secondContent$ می‌گیرد که می‌توان به‌ ترتیب آن‌ها را به همان مقالات A و B تعبیر کرد. در خط دوم،‌ متغیری ساخته‌ایم تحت‌ عنوان dotProduct$ که قرار است حاصل‌ضرب داخلی این دو پارامتر (بُردار) را در خود ذخیره سازد.

در زبان برنامه‌نویسی PHP تابعی از پیش تعریف شده داریم تحت‌عنوان ()array_intersect که دو پارامتر ورودی می‌گیرد و کلید‌های مشابه را مشخص می‌سازد. در این مثال، کلید tags در پارامترهای ورودی شامل آرایه‌ای از تگ‌های مرتبط با هر مقاله است که به جای هر دو پارامتر ورودی این فانکشن (تابع) در نظر گرفته شده سپس خروجی این تابع را داخل تابع دیگری از PHP تحت‌عنوان ()count قرار داده‌ایم که اندازهٔ یک آرایه را مشخص می‌سازد و در نهایت خروجی در متغیر dotProduct$ ذخیره می‌شود.

سپس متغیر دیگری در خط سوم تحت‌ عنوان cosineSimilarity$ ایجاد کرده و مقدار آن را برابر با حاصل تقسیم متغیر dotProduct$ بر جذر تعداد تگ‌های مقاله‌ٔ A ضرب در جذر تعداد تگ‌های مقالهٔ B قرار داده و در نهایت در خط چهارم مقدار متغیر cosineSimilarity$ را به اصطلاح return کرده‌‌ایم. اکنون جهت تست علمکرد این تابع، آرایه‌های زیر را در نظر می‌گیریم:

$firstContent = [ 
 'tags' => ['programming', 'open source', 'python', 'micropython'] 
]; 

$secondContent = [ 
 'tags' => ['programming', 'editor'] 
]; 

echo calSimilarity($firstContent, $secondContent);

و به‌ عنوان خروجی کد فوق داریم:

0.35355339059327

می‌بینیم که بر اساس فرمول فوق، این تابع به‌ درستی کار کرده و تقریباً همان خروجی که روی کاغذ به دست آورده بودیم را در اختیارمان قرار داده است.

از این پس به سادگی می‌توان یک کِران‌جاب تعریف کرد تا پشت پرده دائم در حال مقایسهٔ مقالات مختلف بوده و نتایج را در جدولی مثلاً تحت عنوان content_similarity_index ذخیره سازد و به راحتی می‌توان در کوئری خود گفت که مثلاً پست‌هایی که میزان مشابهت‌ آن‌ها بالای 0.70 است را در معرض دید کاربران قرار دهد (همان‌طور که در مقاله MicroPython: نسخهٔ کاستومایز شده‌ای از زبان پایتون برای دیوایس‌های اِمبدد مشاهده می‌کنید، مقالاتی که به عنوان پست‌های مرتبط از دیتابیس فراخوانی شده‌اند تا حد امکان به نوعی با پایتون مرتبط هستند.)