Graph چیست و این دیتا استراکچر چه کاربردهایی دارا است؟

به طور کلی، دیتا استراکچرها یکسری فرمت خاص به منظور سازمان‌دهی و ذخیره‌سازی داده‌ها هستند که هر یک در راستای نگهداری داده‌ها به منظور انجام پردازش‌های مد نظر روی دیتای مربوطه طراحی شده‌اند تا بتوان با روش‌های مناسب و از آن مهم‌تر بهینه به دیتای مورد نظر دسترسی پیدا کرده و عملیات مربوطه را با به‌کارگیری الگوریتم‌های مختلف روی آن‌ها انجام داد. دیتا استراکچرها انواع مختلفی دارند که از آن جمله می‌توان به آرایه‌، گراف‌، پُشته و مواردی از این دست اشاره کرد که در ادامۀ این مقاله قصد داریم تا با دیتا استراکچر گراف آشنا شده و کاربردهای آن به منظور نگهداری دیتا را مورد بررسی قرار دهیم.

آشنایی با دیتا استراکچر گراف

Graph دیتا استراکچری است که به منظور مدل‌سازی مجموعه‌ای از اشیاء و ارتباطات مابین آن‌ها مورد استفاده قرار می‌گیرد و بر اساس نماد ریاضیاتیِ (G(V, E نمایش داده می‌شود که در آن V اشاره بر اصطلاحاً Vertices یا مجموعۀ رئوس گراف دارد و E سرواژۀ عبارت Edges بوده و مجموعه یال‌های گراف مد نظر را شامل می‌شود. به عنوان یک مثال کاربردی از گراف‌ها می‌توان مدل‌سازی روابط مابین افراد در #شبکه‌های اجتماعی را نام برد که در آن تک‌تک افراد به منزلۀ رئوس گراف در نظر گرفته شده و ارتباطات مابین ایشان نیز توسط خطوطی نمایش داده می‌شوند که دو یا چند رأس از گراف مد نظر را به هم وصل کرده و تحت عنوان یال شناخته می‌شوند.

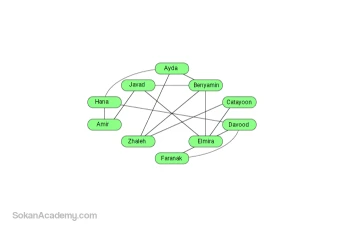
در واقع، وجود ارتباط مابین برخی از رئوس گرافِ شبکۀ اجتماعی بدین معنی است که افراد متناظر این رئوس یکدیگر را می‌شناسند و بالعکس؛ به عبارت دیگر، اگر یالی مابین رئوس گراف وجود نداشته باشد بدین معنی است که افراد مذکور با یکدیگر آشنایی ندارند که برای درک بهتر این موضوع، تصویر فوق را مد نظر قرار می‌دهیم.

این تصویر مثالی بسیار کوچک از گراف یک شبکۀ اجتماعی است که در آن هر یک از افراد با رئوس گراف و ارتباطات مابین ایشان نیز توسط یال‌هایی مدل‌سازی شده‌ است که این یال‌ها برخی از رئوس گراف را به هم متصل می‌کنند به طوری که ارتباط مابین دو رأس فرضی از گراف مد نظر تحت عناوین u و v را با نماد (u, v) نشان می‌دهیم که به منزلۀ وجود یالی از رأس u به v می‌باشد. به طور مثال، در گراف فوق یالی بین امیر و جواد وجود دارد که آن را به صورت (Amir, Javad) نشان می‌دهیم. به علاوه اینکه ارتباطات مابین رئوس شبکۀ فوق دوسویه بوده و بدین معنی است که چنانچه فردی همچون امیر با فرد دیگری مانند جواد ارتباط داشته باشد، امیر او را می‌شناسد و بدین ترتیب جواد نیز با امیر آشنایی دارد و به تعبیری می‌توان گفت که این گراف بی‌جهت است.

به طور کلی، گراف‌ها را می‌توان در دو دستۀ به اصطلاح Directed (جهت‌دار) و Undirected (بی‌جهت) تقسیم‌بندی کرد که در گراف‌های بی‌جهت ارتباطات مابین رئوس گراف دوسویه می‌باشد و در مورد مثال فوق نیز همان‌طور که پیش‌تر اشاره کردیم، ارتباطات از نوع بی‌جهت بوده و می‌توان گفت که گراف مد نظر یک گراف بی‌جهت می‌باشد؛ بنابراین یال (u, v) مابین دو رأس u و v از گراف بی‌جهت را می‌توان با رابطۀ (v, u) نیز نمایش داد به علاوه اینکه در گراف‌های بی‌جهت دو رأسی که با یکدیگر ارتباط دارند و توسط یالی به هم متصل شده‌اند، اصطلاحاً Adjacent یا رئوس مجاور و همسایۀ یکدیگر به شمار می‌روند. همچنین تعداد یال‌های متصل به یک رأس در گراف بی‌جهت اصطلاحاً Degree یا درجۀ آن رأس نامیده می‌شود (در ادامۀ این مقاله با گراف‌های جهت‌دار نیز آشنا خواهیم شد که در آن‌ها ارتباطات مابین رئوس گراف لزوماً دوسویه نمی‌باشند.)

اکنون مجدداً مثال شبکۀ اجتماعی فوق را در نظر می‌گیریم. همان‌طور که می‌بینید، هیچ یال مستقیمی مابین رئوسی به نام‌های آیدا و فرانک وجود ندارد بدین معنی که این دو فرد یکدیگر را نمی‌شناسند. حال فرض کنید آیدا قصد دارد تا با فرانک آشنا شود که چنین مواردی در دنیای واقعی نیز بسیار اتفاق می‌افتد به طوری که بسیاری از ما با برخی افراد از طریق دوستان مشترک خود آشنا می‌شویم؛ به عبارت دیگر، در شبکۀ اجتماعی فوق آیدا و فرانک می‌توانند از طریق دوستان مشترک خود و آشنایی فرانک با المیرا و المیرا با بنیامین با یکدیگر آشنا شوند.

در واقع، مسیری متشکل از سه یال مابین رئوسی با نام‌های فرانک و آیدا وجود دارد که مستقیم‌ترین و همچنین کوتاه‌ترین به اصطلاح Path (مسیر) برای برقراری ارتباط مابین این دو فرد است به طوری که هیچ مسیر دیگری مابین دو رأس مذکور با طول کمتر از سه یال وجود ندارد که چنین مسیرهایی در گراف تحت عنوان Shortest Path (کوتاه‌ترین مسیر) شناخته می‌شوند که مسیری مابین دو رأس با کمترین تعداد یال را مشخص می‌کنند به طوری که کوتاه‌ترین مسیر مذکور مابین دو رأس آیدا و فرانک را در تصویر زیر مشخص کرده‌ایم:

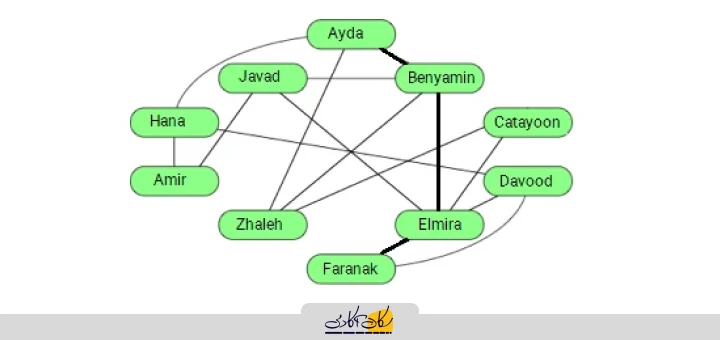
همچنین مسیری که از یک رأس خاص در گراف شروع شده و با گذر از سایر رأس‌های گراف به خود آن بازمی‌گردد تحت عنوان Cycle (حلقه) شناخته می‌شود و همان‌طور که در تصویر زیر مشاهده می‌کنید، مسیری از رأس آیدا شروع شده و با گذر از رئوس بنیامین، المیرا، جواد، امیر و حنا مجدداً به رأس آیدا بازمی‌گردد که این مسیر یکی از چند حلقه‌ای است که در گراف شبکۀ اجتماعی فوق وجود دارد اما این در حالی است که کوتاه‌ترین حلقه برای رأس آیدا از این رأس شروع شده و با گذر از رئوس بنیامین و ژاله مجدداً به رأس مذکور بازمی‌گردد که در ادامه این حلقه را روی گراف مذکور مشخص کرده‌ایم:

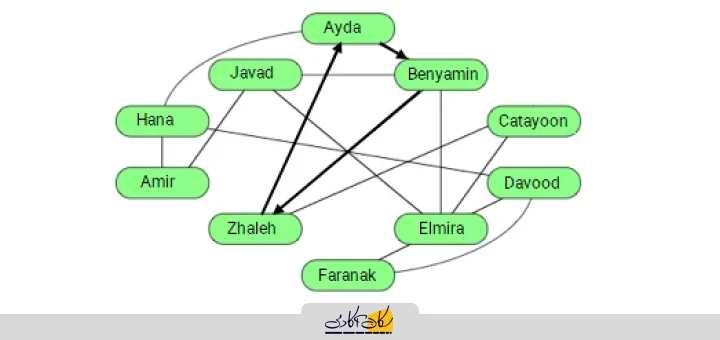
در برخی موارد نیز گرافی داریم که روی هر یک از یال‌های آن مقادیر عددی نوشته می‌شوند به طوری که این اعداد بیانگر ارزش ارتباط مابین دو رأس متناظر می‌باشند. برای مثال، در یک گراف شبکۀ اجتماعی اعداد روی یال‌ها را می‌توان به منظور نشان دادن میزان شناخت هر فرد از فردی دیگر به کار برد یا به عنوان مثالی دیگر نقشۀ راه‌های بین‌شهری را در نظر می‌گیریم و فرض می‌کنیم که جادۀ یک‌طرفه مابین هیچ شهری نداریم و از همین روی گراف مد نظر به منظور مدل‌سازی نقشۀ مذکور یک گراف بی‌جهت است که در آن هر یک از شهرها با رئوس گراف و جاده‌های مابین آن‌ها نیز به عنوان یال‌های گراف مدل‌سازی می‌شوند به طوری که مقادیر روی هر یک از یال‌ها بیانگر فاصلۀ مابین شهرها می‌باشند.

برای نمونه، در ادامه نقشه‌ای در مقیاس کوچک از جاده‌های مابین برخی شهرهای ایران داریم که فاصلۀ مابین هر دو شهر به طور تقریبی و بر حسب کیلومتر روی یال‌های متصل‌کنندۀ دو رأس متناظر نوشته شده است که در اصطلاح ریاضیاتی هر یک از مقادیر عددی روی یال‌ها Weight یا وزن آن یال نامیده شده و بدین ترتیب گرافی که یال‌های آن مقادیر عددی دارند، گراف وزن‌دار نامیده می‌شود:

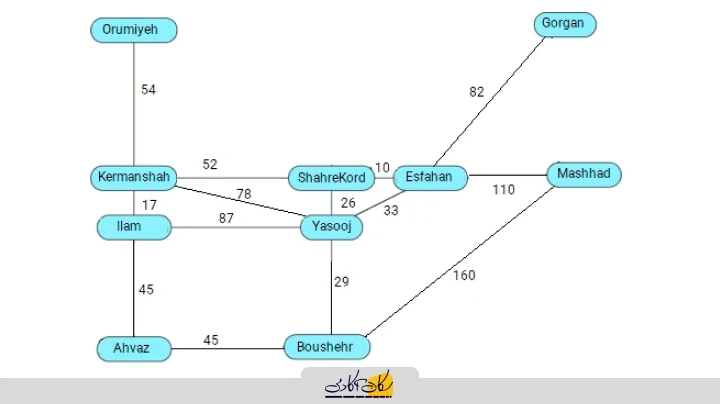
در نقشۀ فوق، اگر بخواهیم کوتاه‌ترین مسیر مابین دو شهر خاص را بیابیم می‌باید مسیری پیدا کنیم مجموع وزن یال‌ها در آن کمترین مقدار را در میان تمامی مسیرهای مابین دو شهر مذکور داشته باشد (در همین راستا، می‌توانید به آموزش پیاده‌سازی الگوریتم Dijkstra جهت یافتن مسیر بهینه مابین رئوس گراف در پایتون مراجعه نمایید.)

آشنایی با گراف جهت‌دار

ارتباط مابین رئوس یک گراف همواره دوسویه نمی‌باشد که برای نمونه می‌توان نقشۀ بین‌شهری مربوط به مثال قبل را نام برد با این تفاوت که جاده‌های بین‌شهری را در آن یک‌طرفه در نظر می‌گیریم. به عنوان مثالی دیگر، تصویر زیر را مد نظر قرار می‌دهیم که در آن ترتیب مراحل مورد نیاز به منظور ساخت یک بنای ساختمانی را با به‌کارگیری دیتا استراکچر گراف مدل‌سازی کرده‌ایم:

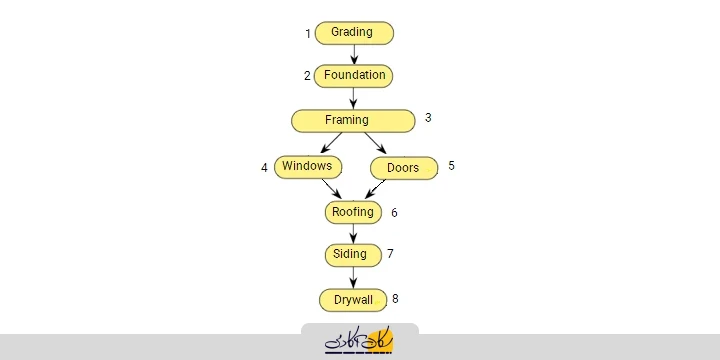
همان‌طور که در تصویر فوق مشاهده می‌کنید، یال‌های مابین رئوس با پیکان مشخص شده‌اند بدین معنی که ارتباط مابین آن‌ها جهت‌دار بوده و بدین ترتیب گراف فوق یک گراف جهت‌دار می‌باشد.

در واقع، دلیل استفاده از گراف جهت‌دار برای مدل‌سازی مثال فوق‌الذکر این بوده که چنین گرافی قابلیت مشخص‌سازی ترتیب ساخت یک ساختمان را دارا است. برای مثال، یالی که رأس مربوط به Foundation (پی‌ریزی) را به رأس Framing (چارچوب) وصل می‌کند به منظور نشان دادن اولویت پی‌ریزی یک بنای ساختمانی قبل از ساخت اسکلت آن مورد استفاده قرار گرفته است و اعداد کنار هر رأس نیز مشخص‌کنندۀ ترتیب اولویت رئوس در هر سطح می‌باشند؛ بدین صورت که در مثال فوق Grading (مسطح‌سازی محل ساخت‌وساز) سپس پی‌ریزی ساختمان و در ادامه ساخت اسکلت آن و به همین ترتیب رئوس بعدی از اولویت بالاتری برخوردار هستند.

همان‌طور که می‌بینید، گراف جهت‌دار فوق هیچ حلقه‌ای ندارد که چنین گراف‌هایی را تحت عنوان Directed Acyclic Graph یا به اختصار DAG به معنای «گراف جهت‌دار بدون حلقه» می‌نامند به علاوه اینکه امکان ساخت گراف‌های وزن‌دار جهت‌دار نیز وجود دارد و برای نمونه می‌توان نقشۀ جادۀ مثال پیشین را نام برد که اگر جاده‌های بین‌شهری در آن را یک‌طرفه فرض شود، وزن گراف نیز فاصلۀ مابین شهرها را مشخص می‌کند.

نکتۀ قابل‌توجه در مورد یال‌های گراف جهت‌دار این است که اصطلاح متفاوتی برای یال‌ها در گراف‌های جهت‌دار به کار گرفته می‌شود به طوری که یال‌های جهت‌دار از یک رأس در گراف خارج شده و به رأس دیگری وارد می‌شوند. برای نمونه، در مثال فوق‌ یک یال جهت‌دار از رأس Foundation (پی‌ریزی) خارج و وارد رأس مربوط به Framing (چارچوب) ساختمان می‌شود و از همین روی یال جهت‌دار از رأس u به v را با جفت (u, v) نمایش می‌دهیم که در آن بر خلاف گراف‌های بی‌جهت، ترتیب رئوس بسیار مهم می‌باشد. همچنین تعداد یال‌هایی که از یک رأس خاص خارج می‌شوند را اصطلاحاً Out-degree یا درجۀ خروجی آن رأس و تعداد یال‌های ورودی به رأس مد نظر را In-degree یا درجۀ ورودی آن می‌نامند.

اندازۀ گراف

به منظور اِعمال یک الگوریتم روی دیتا استراکچر گراف نیاز است تا از اندازۀ رئوس و یال‌های گراف مد نظر مطلع باشیم تا بتوانیم زمان مورد نیاز برای اجرای الگوریتم و همچنین فضای مورد نیاز برای نگهداری دیتا استراکچر مربوطه را مشخص سازیم. همان‌طور که در ابتدای این مقاله اشاره کردیم، مجموعۀ رئوس گراف را با نماد V و مجموعۀ یال‌ها را با E نمایش می‌دهیم و اگر فرض کنیم که پیچیدگی زمانی الگوریتمی خاص روی گراف مد نظر از مرتبۀ |V| باشد بدین معنی که اجرای هر خط از الگوریتم مذکور روی گراف مربوطه حدود |V| زمان به خود اختصاص می‌دهد، نماد | | به منظور نمایش اندازۀ مجموعۀ رئوس گراف مربوطه مورد استفاده قرار گرفته است.

نحوۀ ذخیره‌سازی و نگهداری دیتا استراکچر گراف

روش‌های مختلفی برای نمایش و ذخیره‌سازی دیتا استراکچر گراف وجود دارد که هر کدام مزایا و معایب خاص خود را داشته و متناسب با الگوریتم‌های متفاوتی مورد استفاده قرار می‌گیرند که بسته به شرایط مختلف روی دیتای ورودی اجرا می‌شوند و از همین روی در ادامه قصد داریم تا سه روش پرکاربرد به منظور نگهداری و نمایش دیتا استراکچر گراف را معرفی کرده و هر یک را از جنبه‌هایی مورد بررسی قرار دهیم که عبارتند از:

- حافظۀ مورد نیاز سیستم برای اجرای هر الگوریتم به منظور نگهداری یا نمایش گراف
- زمان مورد نیاز برای پیدا کردن یال مد نظر در گراف مربوطه
- زمان مورد نیاز برای پیدا کردن همسایه‌های یک رأس خاص از آن گراف

به طور کلی، نام‌گذاری رأس‌های گراف با به‌کارگیری اعداد کاربردی‌تر بوده و در آن به جای نام‌هایی همچون آیدا، اصفهان یا چارچوب از اعداد برای نام‌گذاری رئوس استفاده می‌شود که در چنین شرایطی می‌توان گفت که گرافی به تعداد |V| رأس شامل رئوسی می‌باشد که با اعدادی در بازۀ 0 تا V| - 1| نام‌گذاری شده‌اند:

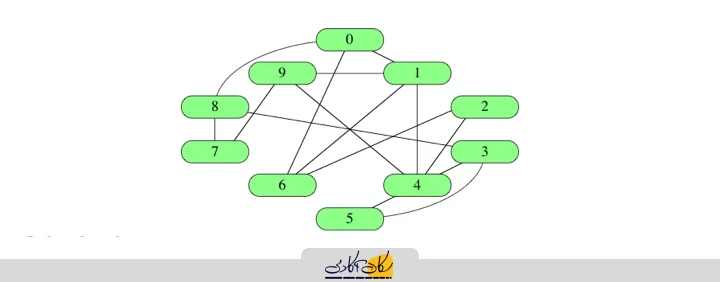
و همان‌طور که در تصویر فوق می‌بینید، یک گراف شبکۀ اجتماعی متشکل از 10 رأس داریم که رئوس آن را با اعدادی متعلق به بازۀ 0 تا 9 نام‌گذاری کرده‌ایم.

نگهداری دیتا استراکچر گراف با به‌کارگیری Edge List

روشی ساده برای نمایش و ذخیره‌سازی دیتا استراکچر گراف به‌کارگیری آبجکتی از جنس لیست یا آرایه‌ای متشکل از مجموعه یال‌های گراف به تعداد |E| است که برای ذخیرۀ هر یال از گراف مربوطه آرایه‌ای متشکل از دو عدد تعریف کرده و نام رئوس متناظر از یال مد نظر را در آن نگهداری می‌کنیم؛ به عبارت دیگر، آرایه‌ای داریم که شامل نام رئوسی از گراف می‌باشد که توسط یال مربوطه به یکدیگر متصل شده‌اند مضاف بر اینکه اگر یال‌های گراف وزن داشته باشند، اِلِمان سومی به منظور ذخیرۀ وزن یال را به آرایۀ مذکور اضافه می‌کنیم.

بنابراین هر یال حاوی تنها دو یا سه عدد می‌باشد و از همین روی می‌توان گفت که فضای لازم برای ذخیره‌سازی و نگهداری دیتا استراکچر گراف با به‌کارگیری لیست یال‌های آن معادل تعداد یال‌های گراف یا |E| می‌باشد که در ادامه یک نمونه از نحوۀ ذخیره‌سازی دیتا استراکچر گراف شبکۀ اجتماعی فوق را با به‌کارگیری لیست یال‌های آن آورده‌ایم:

[
 [0, 1], [0, 6], [0, 8], [1, 4], [1, 6], 
 [1, 9], [2, 4], [2, 6], [3,4], [3, 5],
 [3, 8], [4, 5], [4, 9], [7, 8], [7, 9]
]

ذخیره‌سازی و نگهداری گراف با به‌کارگیری لیست یال‌های آن بسیار ساده است اما فرض کنید که بخواهیم بررسی کنیم که آیا یک یال خاص در گراف مربوطه وجود دارد یا خیر که برای این منظور باید تمامی لیست را جستجو کنیم و چنانچه یال‌های ذخیره‌شده در این لیست از ترتیب خاصی برخوردار نباشند، مجبور به انجام جستجویی معادل با تعداد یال‌های گراف یا به عبارت دیگر تعداد |E| جستجو در لیست هستیم که کاری زمان‌بر است!

نگهداری دیتا استراکچر گراف با به‌کارگیری Adjacency Matrix

ماتریس مجاورت یا همسایگی برای گرافی با |V| رأس، ماتریسی معادل |V| سطر و |V| ستون است؛ به عبارت دیگر، ماتریسی به اندازۀ |V|x|V| داریم که تعداد سطرها و ستون‌های آن برابر با تعداد رئوس گراف مربوطه می‌باشد و تمامی اِلِمان‌های آن 0 یا 1 هستند به طوری که اگر اِلِمان مربوط به سطر i و ستون j برابر با 1 باشد بدین معنی است که در گراف متناظر یالی به صورت (i, j) از رأس i به رأس j داریم و بالعکس.

همچنین در صورتی که گراف مد نظر یک گراف وزن‌دار باشد، اِلِمان مربوط به سطر i و ستون j معادل عدد مربوط به وزن یال مربوطه قرار داده می‌شود که در چنین شرایطی برای نمایش عدم اتصال دو رأس خاص یک مقداری قراردادی همچون null یا خالی در نظر گرفته می‌شود. در ادامه Adjacency Matrix (ماتریس مجاورت) برای گراف شبکۀ اجتماعی فوق‌ را آورده‌ایم:

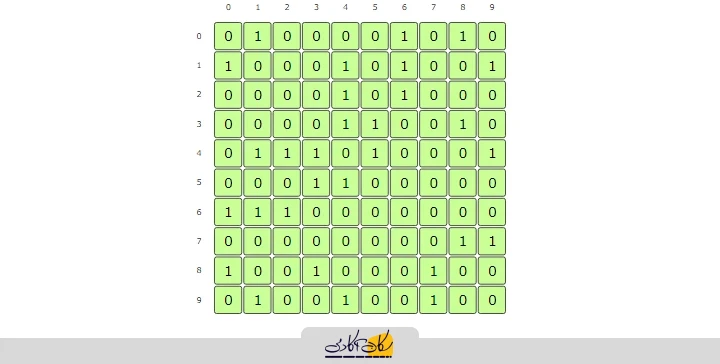
جستجوی یک اِلِمان خاص در ماتریس مجاورت بسیار ساده می‌باشد چرا که کافی است تا آن را از سطر مربوطه و در ستون مد نظر جستجو کرد. به عنوان مثال، در ماتریس مجاورت فوق می‌توانیم با بررسی اِلِمان سطر i و ستون j از ماتریس مربوطه ببینیم که آیا یال (i, j) در گراف وجود دارد یا خیر.

در عین حال، می‌توان گفت که ذخیره‌سازی دیتا استراکچر گراف با به‌کارگیری ماتریس مجاورت نقاط ضعفی نیز دارا است که از آن جمله می‌توان به فضای مورد نیاز برای نگهداری گراف اشاره که معادل آرایه‌ای دوبُعدی به ابعاد |V|x|V| می‌باشد به طوری که حتی برای ذخیره‌سازی گراف‌های بسیار کوچک نیاز به فضایی در ابعاد |V|x|V| داریم. به عنوان مثال، می‌توان گراف‌هایی را نام برد که تعداد کمی از رئوس آن به یکدیگر متصل می‌باشند و از همین روی در ماتریس مجاورت متناظر تعداد اِلِمان‌های بسیار کمی مقدار عددی معادل 1 دارند (چنین گراف‌هایی اصطلاحاً Sparse نام داشته و در آن‌ها تعداد بسیار کمی از رئوس گراف توسط یالی به یکدیگر متصل می‌شوند.) اما به هر حال برای نگهداری گراف‌های اِسپارس نیز به فضایی با ابعاد |V|x|V| نیاز داریم؛ به عبارت دیگر، برای یک گراف به اصطلاح اِسپارس، اِلِمان‌های ماتریس مجاورت عمدتاً 0 هستند و این در حالی است که برای ذخیره‌سازی تنها چند یال غیر 0 مجبور به اِشغال فضای بسیار زیادی هستیم که اساساً می‌توان گفت این روش بهینه نیست!

به علاوه اینکه اگر بخواهیم رئوس همسایۀ یک رأس فرضی همچون i از گراف مد نظر را مشخص کنیم، باید تمام |V| اِلِمان مربوط به سطر i از ماتریس مجاورت را جستجو و بررسی کنیم تا ببینیم چه اِلِمانی مقدار معادل 1 دارد و حتی در شرایطی که گراف مد نظر یک گراف اسپارس است که احتمالاً تعداد کمی از رئوس آن با رأس فرضی i مجاور هستند نیز باید تمامی اِلِمان‌های سطر i را به منظور پیدا کردن اِلِمانی از ستون j با مقدار عددی 1 جستجو کنیم.

در مورد گراف‌های بی‌جهت، ماتریس مجاورت یک ماتریس متقارن است بدین معنی که چنانچه اِلِمان مربوط به سطر i و ستون j برابر با 1 باشد، اِلِمان سطر j و ستون i از این ماتریس نیز برابر با 1 است چرا که یالی بی‌جهت مابین رئوس برقرار بوده و اتصال رأس i به j معادل برقراری ارتباط رأس j به i می‌باشد اما برای گراف‌های جهت‌دار ماتریس همسایگی لزوماً متقارن نمی‌باشد.

نگهداری دیتا استراکچر گراف با به‌کارگیری Adjacency List

نمایش و ذخیره‌سازی دیتا استراکچر گراف با استفاده از Adjacency List (لیست مجاورت) ترکیبی از ذخیره‌سازی گراف مربوطه با به‌کارگیری ماتریس مجاورت و لیستی از یال‌های آن می‌باشد به طوری که برای هر رأس i از گراف مد نظر آرایه‌ای متشکل از رئوس همسایۀ آن را ذخیره می‌کنیم. در واقع، به ازای هر یک از رئوس گراف آرایه‌ای به اندازۀ |V| داریم که لیست مجاورت رأس مد نظر بوده و نام رئوس مجاور در این لیست نگهداری می‌شوند که در ادامه لیست مجاورت مربوط به گراف شبکۀ اجتماعی فوق‌الذکر را آورده‌ایم:

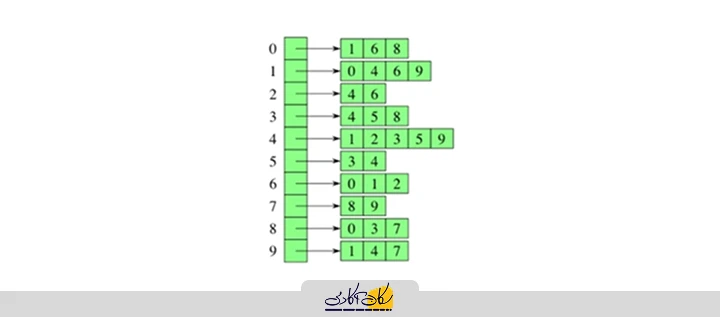
در این روش، دست‌یابی به لیست مجاورت هر یک از رئوس گراف یا به عبارتی رئوس همسایۀ آن‌ها بسیار ساده می‌باشد چرا که کافی است تا در آرایۀ مد نظر به دنبال اِلِمانی با اندیس رأس مربوطه بگردیم. همچنین برای بررسی اینکه آیا یالی همچون (i, j) در گراف وجود دارد یا خیر، به لیست مجاورت رأس i از آرایۀ مد نظر رجوع کرده و در داخل لیست مربوطه به دنبال اِلِمان j می‌گردیم (لازم به یادآوری است که برای ذخیره‌سازی رئوس گراف در لیست مجاورت نیازی به رعایت ترتیب خاصی به ازای شمارۀ هر یک از رئوس گراف نداریم اما به هر حال بهتر است که آن‌ها را به ترتیب صعودی ذخیره کنیم.)

الگوریتم مربوطه برای بررسی وجود یالی مابین دو رأس فرضی i و j از گراف مد نظر نیاز به زمانی معادل d دارد که در آن d برابر با درجۀ رأس i می‌باشد بدین معنی که تمامی یال‌های خروجی از رأس i می‌باید جستجو شده و اتصال آن‌ها به رأس فرضی j مورد بررسی قرار گیرد. به عبارت دیگر، برای بررسی وجود یالی همچون (i, j) به زمانی معادل d برای پیمایش لیست مجاورت رأس i داریم چرا که باید بررسی کنیم ببینیم که در این لیست اِلِمان j مقدار عددی معادل 1 دارد یا خیر. همچنین درجۀ رأس فرضی i از گراف مد نظر حداکثر برابر با V| - 1| است بدین معنی که یک رأس از گراف می‌تواند با تمامی رئوس ارتباط داشته و توسط یالی به هر یک از آن‌ها متصل باشد که در چنین شرایطی رأس i با تمامی V| - 1| رأس گراف همسایه می‌باشد مضاف بر اینکه یک رأس گراف می‌تواند درجه‌ای معادل 0 داشته و با هیچ یک از رئوس دیگر گراف ارتباط نداشته باشد که در این صورت اصطلاحاً رأس Isolated (ایزوله) نامیده می‌شود.

در گراف‌های بی‌جهت در صورتی که رأسی همچون j در لیست مجاورت رأس i قرار گیرد بدین معنی است که مابین رئوس j و i ارتباطی برقرار است و از همین روی رأس i با j با یکدیگر نیز ارتباط داشته و بدین ترتیب می‌توان گفت که رأس i نیز در لیست مجاورت رأس j قرار دارد به علاوه اینکه چنانچه گراف مد نظر یک گراف وزن‌دار باشد، هر یک از آیتم‌های ذخیره‌شده در لیست مجاورت را به صورت یک آرایه دوتایی متشکل از شمارۀ رأس و وزن یال مربوطه را ذخیره می‌کنیم.

بنابراین برای ذخیره‌سازی لیست مجاورت، به تعداد رئوس گراف یا |V| لیست داریم که هر لیست می‌تواند حداکثر تعداد V| - 1| رأس داشته باشد و از همین روی می‌توان گفت که یک لیست مجاورت برای ذخیره‌سازی گراف بی‌جهت دارای تعداد اِلِمان‌های زیر است:

2|E| 

در واقع، هر یال فرضی به صورت (i, j) دقیقاً دو مرتبه در لیست‌های مجاورت تکرار می‌شود به طوری که یک بار در لیست مربوط به اِلِمان i و بار دیگر در لیست مجاورت اِلِمان j ذکر می‌شود و هر یک از این لیست‌ها نیز به تعداد |E| یال دارند اما برای گراف‌های جهت‌دار، لیست‌های مجاورت شامل |E| اِلِمان هستند که هر اِلِمان مربوط به یک یال جهت‌دار از گراف مربوطه می‌باشد.

جمع‌بندی
در این مقاله به بررسی ديتا استراكچر گراف پرداخته و برخی از روش‌‌های پرکاربرد به منظور نگهداری و ذخیره‌سازی آن را تشریح کردیم و همچنین چند مثال از کاربردهای این دیتا استراکچر در دنیای واقعی را بیان کردیم که از آن جمله می‌توان به مسئلۀ یافتن کوتاه‌ترین مسیر مابین دو رأس گراف اشاره کرد.