درختان، یکی از مهمترین ساختارهای داده غیرخطی هستند که گرههایی را تعریف میکنند که از طریق یالها به یکدیگر متصل میشوند. هر درخت دودویی (Binary Tree) از یک گره ریشه به عنوان گره والد، گره چپ و گره راست، به عنوان گره فرزند (Child) تشکیل شده است. لازم به توضیح است که درخت جستوجوی باینری، درختی است که امکان جستوجوی سریع، درج و حذف دادههای مرتب شده را امکان پذیر میکند. همچنین، زمان یافتن یک گره را به میزان قابل توجهی کوتاه میکند.
درخت، ساختار دادهای است که در آن عناصر دادهای بر مبنای رویکرد سلسله مراتبی به یکدیگر متصل شده و نشان داده میشوند. هر درخت یک گره ریشه دارد که از طریق آن میتوانیم به هر عنصر درخت دسترسی داشته باشیم. (برای آشنایی بیشتر با ساختار دادهی درخت به مقالهی ساختار داده درخت (Tree) چیست و چگونه آن را در پایتون پیادهسازی کنیم؟ مراجعه کنید.) هنگامی که درختی را از گره ریشه به سمت پایین پیمایش میکنیم، هر گره شامل صفر یا چند گره میشود که گرههای فرزند (child) نام دارند. یک درخت دودویی ساده را میتوان همانند شکل زیر نشان داد.
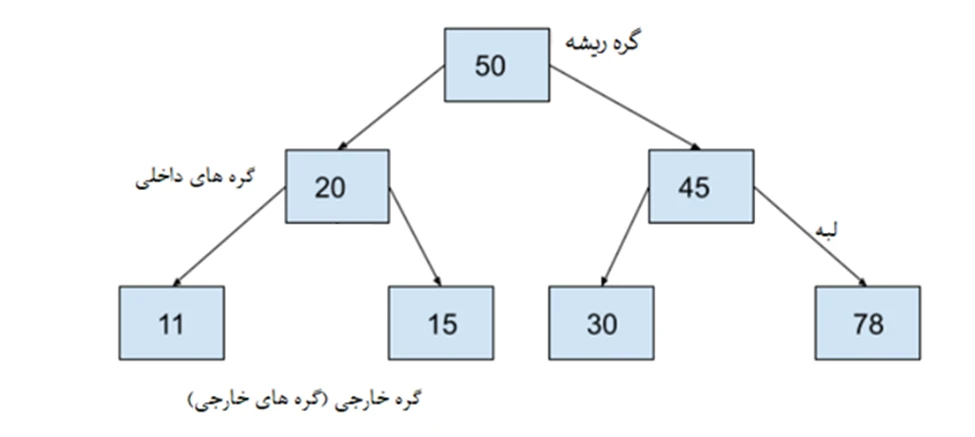
اجزا تشکیل دهنده یک درخت دودویی
همانگونه که در شکل بالا مشاهده میکنید، درختان در پایتون در حالت پایه از گره ریشه، گرههای برگ و گرههای داخلی تشکیل شدهاند. هر گره از طریق یک مرجع (reference) که به آن یال (Edge) میگویند به گره لبه متصل میشود.
- گره ریشه (Root Node): گره ریشه بالاترین گره یک درخت است. همیشه، اولین گرهای است که هنگام ایجاد درخت ساخته میشود و قادر هستیم از طریق آن به هر عنصر درخت یا بالعکس دسترسی داشته باشیم، گره ریشه است. در شکل بالا، گرهای که مقدار مقدار 50 دارد، گره ریشه است.
- گره والد (Parent Node): گره والد، گرهی است که به گره بعد از خود اشاره دارد. در مثال بالا، 50 والد برای دو گره 20 و 45 است، در حالی که 20 خود والد گرههای 11، 46 و 15 است. به همین ترتیب، 45 والد گرههای 30 و 78 است. به همین دلیل است که همواره گفته میشود، درختها ماهیت سلسله مراتبی دارند.
- گره فرزند (Child Node): گرههای فرزند یک گره والد، گرههایی هستند که گره والد با استفاده از مراجع به آنها اشاره میکند. در شکل بالا، 20 و 45 فرزندان گره 50 هستند. به همین ترتیب، گرههای 11، 46 و 15 فرزندان گره 20 هستند، در حالی که 30 و 78 فرزندان گره 45 هستند.
- یال (Edge): به مکانیزم ارتباطی یک گره والد به یک گره فرزند یال گفته میشود. به زبان ساده، ارتباط میان دو گره را برقرار میکند. در شکل بالا، هر فلشی که هر دو گره را به یکدیگر متصل میکند، یک یال است.
- گره برگ (Leaf Node): گاهی اوقات، گرههایی در درختان وجود دارد که فاقد فرزند هستند. در مثال بالا، 11، 46، 15، 30 و 78 گرههای برگ هستند.
- گرههای داخلی (Internal Nodes): گرههای داخلی، گرههایی هستند که حداقل یک فرزند دارند. در مثال بالا، 50، 20 و 45 گرههای داخلی هستند.
درخت دودویی (Binary Tree) چیست؟
درخت دودویی، یک ساختار داده درختی است که در آن هر گره میتواند حداکثر 2 فرزند داشته باشد. هر گره در یک درخت باینری شامل دادهها و ارجاعهایی به فرزندان خود است. هر دو فرزند با توجه به موقعیتشان به عنوان فرزند چپ (left child) و فرزند راست (right child) نامگذاری می شوند. ساختار یک گره در یک درخت باینری همانند شکل زیر است.
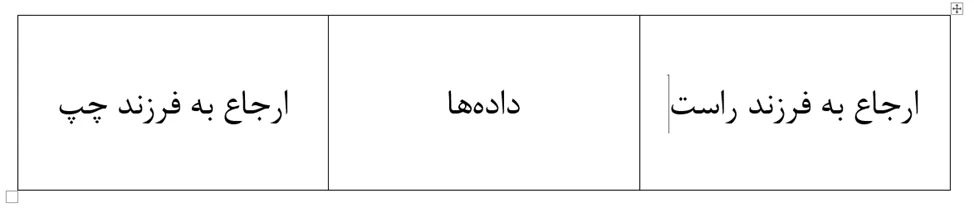
ما میتوانیم یک گره از ساختار نشان داده شده در شکل بالا را در پایتون با استفاده از کلاس زیر تعریف کنیم.
class BinaryTreeNode:
def __init__(self, data):
self.data = data
self.leftChild = None
self.rightChild=Noneدر اینجا تابع سازنده، مقدار داده گره را به عنوان ورودی دریافت میکند، یک شی از نوع BinaryTreeNode ایجاد میکند و فیلد داده را برابر با ورودی دادهها، مقداردهی اولیه میکند و ارجاعها به فرزندان را به None مقداردهی اولیه میکند. این امکان وجود دارد تا در ادامه فرزندان را به گرهها اختصاص داد. نمونهای از یک درخت دودویی در شکل زیر نشان داده شده است.
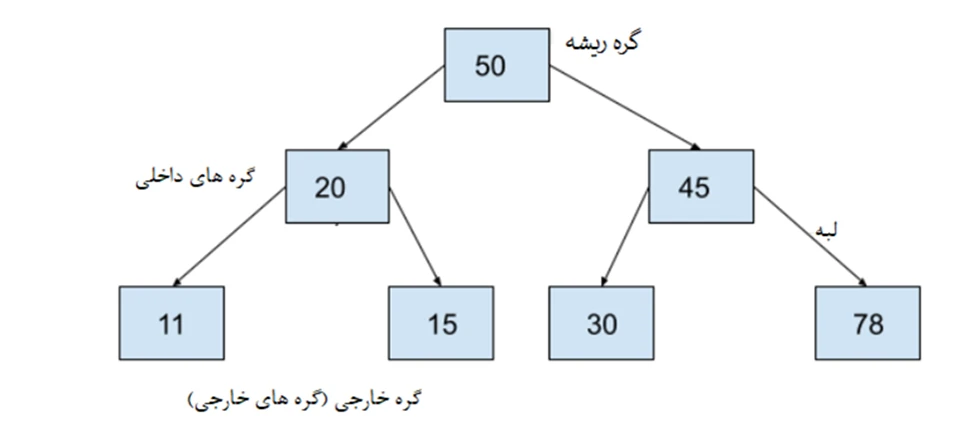
درخت دودویی فوق را میتوانیم به صورت زیر در پایتون پیادهسازی کنیم (برای اجرای کدهای زیر کافی است، محیط توسعه یکپارچه پایتون (IDE) را باز کنید، فایل جدیدی باز کنید، کدها را درون آن تایپ کنید، فایل را ذخیره کنید و روی دکمه Run Module کلیک کنید تا کدها اجرا شوند).
class BinaryTreeNode:
def __init__(self, data):
self.data = data
self.leftChild = None
self.rightChild = None
node1 = BinaryTreeNode(50)
node2 = BinaryTreeNode(20)
node3 = BinaryTreeNode(45)
node4 = BinaryTreeNode(11)
node5 = BinaryTreeNode(15)
node6 = BinaryTreeNode(30)
node7 = BinaryTreeNode(78)
node1.leftChild = node2
node1.rightChild = node3
node2.leftChild = node4
node2.rightChild = node5
node3.leftChild = node6
node3.rightChild = node7
print("Root Node is:")
print(node1.data)
print("left child of the node is:") print(node1.leftChild.data)
print("right child of the node is:") print(node1.rightChild.data)
print("Node is:")
print(node2.data)
print("left child of the node is:") print(node2.leftChild.data)
print("right child of the node is:") print(node2.rightChild.data)
print("Node is:")
print(node3.data)
print("left child of the node is:") print(node3.leftChild.data)
print("right child of the node is:") print(node3.rightChild.data)
print("Node is:")
print(node4.data)
print("left child of the node is:") print(node4.leftChild)
print("right child of the node is:") print(node4.rightChild)
print("Node is:")
print(node5.data)
print("left child of the node is:") print(node5.leftChild)
print("right child of the node is:") print(node5.rightChild)
print("Node is:")
print(node6.data)
print("left child of the node is:") print(node6.leftChild)
print("right child of the node is:") print(node6.rightChild)
print("Node is:")
print(node7.data)
print("left child of the node is:") print(node7.leftChild)
print("right child of the node is:") print(node7.rightChild)خروجی قطعه کد بالا در شکل زیر نشان داده شده است:
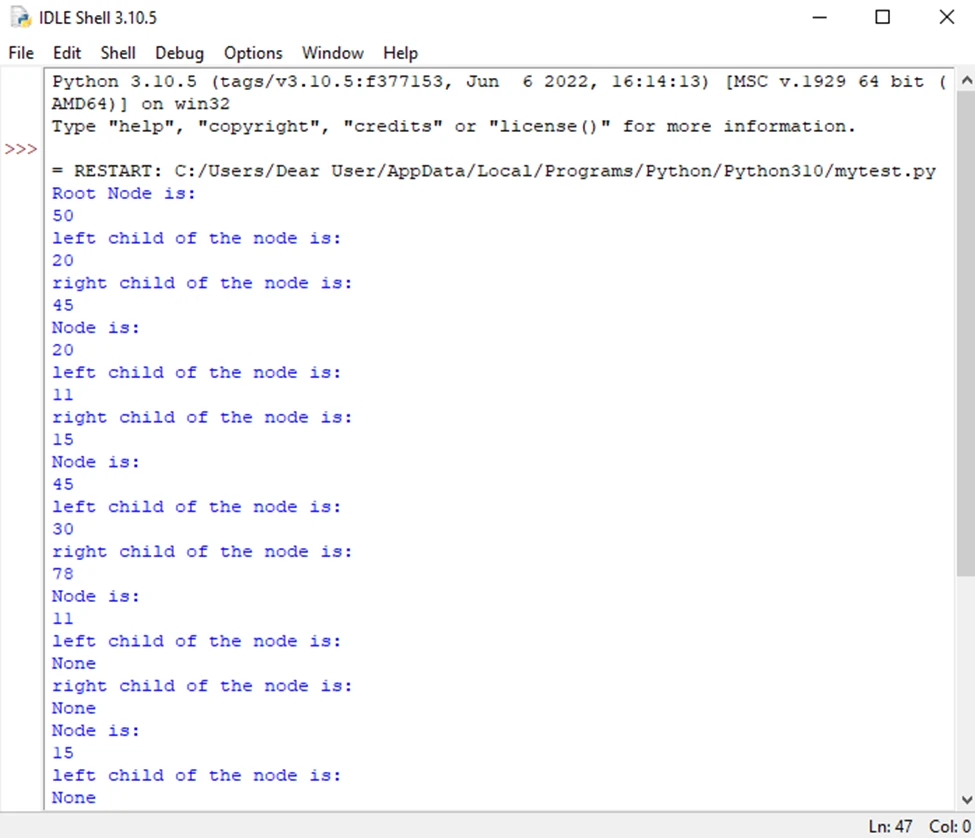
فرآیند درج مقادیر در درخت
یکی از عملیات مهمی که روی درختها انجام میشود، اضافه کردن گرهای به درخت است. متد insert زیر، مقدار گره با گره والد را مقایسه میکند و تصمیم میگیرد که آن را به عنوان گره چپ یا راست اضافه کند. نکته مهمی که باید به آن دقت کنید این است که اگر گره بزرگتر از گره والد باشد، به عنوان یک گره سمت راست درج میشود. در غیر این صورت، در سمت چپ درج میشود. پس از درج گره، در ادامه از متد PrintTree برای چاپ درخت استفاده میکنیم.
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
def insert(self, data):
# Compare the new value with the parent node
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# Print the tree
def PrintTree(self):
if self.left:
self.left.PrintTree()
print( self.data),
if self.right:
self.right.PrintTree()
# Use the insert method to add nodes
root = Node(27)
root.insert(14)
root.insert(35)
root.insert(31)
root.insert(10)
root.insert(19)
root.PrintTree()قطعه کد بالا، گره ریشهای که 27 است را ایجاد میکند. در این درخت، فرزند چپ گره 14 و فرزند راست گره 35 است. خروجی قطعه کد زیر به شرح زیر است:
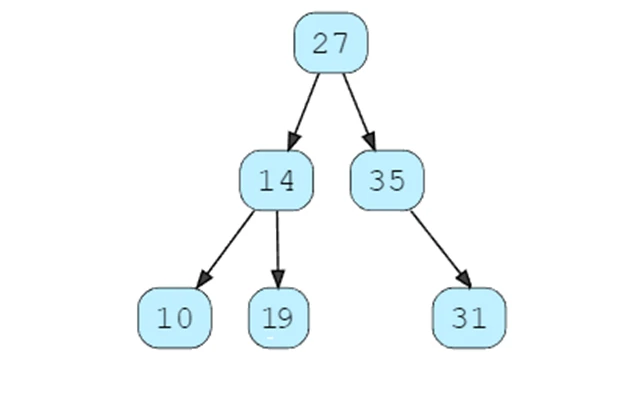
جستوجوی دودویی
همانگونه که پیشتر، اشاره کردیم، ما روشهای مختلفی برای پیمایش و جستوجوی یک مقدار در درخت در اختیار داریم. در قطعه کد زیر، گره را از چپ به راست و با یک والد پیمایش میکنیم.
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert method to create nodes
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# findval method to compare the value with nodes
def findval(self, lkpval):
if lkpval < self.data:
if self.left is None:
return str(lkpval)+" is not Found"
return self.left.findval(lkpval)
elif lkpval > self.data:
if self.right is None:
return str(lkpval)+" is not Found"
return self.right.findval(lkpval)
else:
return str(self.data) + " is found"
# Print the tree
def PrintTree(self):
if self.left:
self.left.PrintTree()
print(self.data),
if self.right:
self.right.PrintTree()
root = Node(27)
root.insert(14)
root.insert(35)
root.insert(31)
root.insert(10)
root.insert(19)
print(root.findval(7))
print(root.findval(14))قطعه کد بالا، درختی که گرههای 10 19 14 27 31 35 دارد را ایجاد میکند. در این درخت گره ۷ وجود ندارد، بنابراین، خروجی قطعه کد فوق به این صورت چاپ میشود که مقدار 7 پیدا نشد. همچنین، به این نکته دقت کنید که 14 گره ریشه فرزند سمت چپ است. خروجی قطعه کد فوق به شرح زیر است:
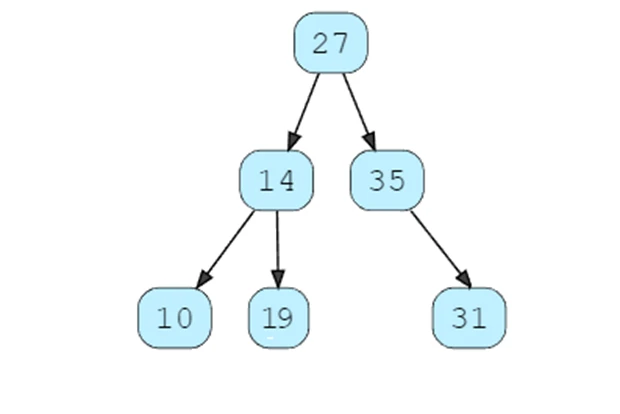
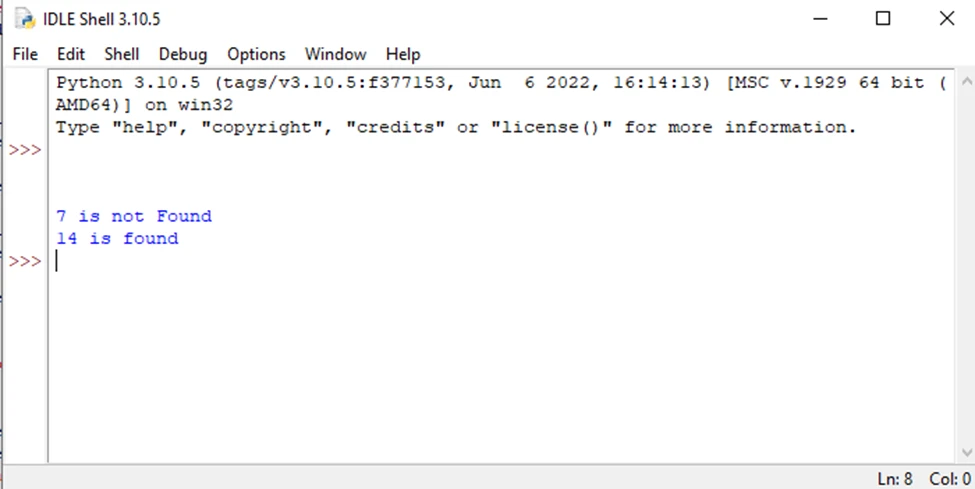
کلام آخر
همانگونه که مشاهده کردید، درختی که عناصر آن حداکثر دو فرزند داشته باشد، درخت دودویی نامیده میشود. هر عنصر در یک درخت دودویی میتواند تنها دو فرزند داشته باشد. گره فرزند چپ باید مقداری کمتر از مقدار والد خود داشته باشد و گره فرزند سمت راست باید مقداری بیشتر از مقدار والد خود داشته باشد. اگر به همین نکته ساده دقت کنید، در زمان پاسخگویی به پرسشهای درختان در کنکور یا درس ساختمان دادهها موفق خواهید شد.