ساختار داده درخت (Tree) چیست و چگونه در پایتون پیاده‌سازی کنیم؟

پایتون از نظر ویژگی‌های کاربردی و ساختارهای داده‌ای که در اختیار برنامه‌نویسان قرار می‌دهد، بسیار غنی است. این زبان برنامه‌نویسی همه ‌منظوره، طیف گسترده‌ای از ساختارهای داده از پیش ساخته شده، مثل لغت‌نامه (dictionary)، فهرست (list)، تاپل (tuple)، مجموعه (set)، frozenset، پشته (stack)، صف (queue)، لیست پیوندی (queue) و غیره را ارائه می‌دهد. 

ساختار داده درخت چیست؟

درخت در پایتون ، یک ساختار داده سلسله مراتبی غیر خطی (non-linear) است که از رئوس (گره‌ها) و یال‌ها (Edge) تشکیل شده است. در ساختارهای داده خطی مثل درخت، پشته، صف و لیست پیوندی عناصر به ترتیب به ساختار داده‌ای افزوده می‌شوند. در ساختارهای داده خطی، هر نوع عملیاتی که روی ساختار داده انجام شود، اندازه داده‌ها را افزایش داده و بر پیچیدگی زمانی (time complexity) می‌افزاید. 

این موضوع باعث می‌شود امکان استفاده از آن‌ها در ارتباط با مسائل دنیای واقعی کمتر شود. به همین دلیل است که برنامه‌نویسان، به سراغ ساختار‌های داده غیرخطی می‌روند تا مانع افزایش پیچیدگی زمانی شوند. لازم به توضیح است که پیچیدگی زمانی به مدت زمانی که طول می‌کشد تا یک الگوریتم اجرا شود، اشاره دارد.

اصطلاحات درختی

شکل زیر مفاهیم مرتبط با درخت‌ها را نشان می‌دهد. 

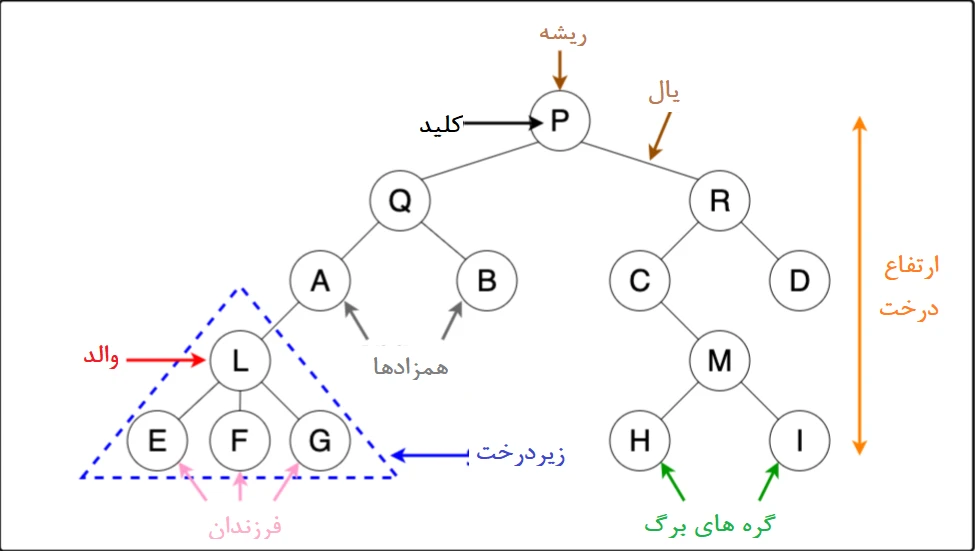
• راس/گره (Vertex/Node): شامل کلید، مقدار یا اشاره‌گرهایی به راس فرزند است. به طور کلی، گره‌هایی که در عمق قرار دارند، گره برگ (leaf node) یا گره خارجی (external node) نامیده می‌شوند. گره‌ای که دارای یک فرزند است و خود زیرریشه است، گره داخلی (internal node) نامیده می‌شود.
• یال‌ها (Edges): ارتباط میان دو گره را برقرار می‌کند. 
• ارتفاع یک درخت (Height of a Tree): به فاصله میان عمیق‌ترین گره تا ریشه اشاره دارد. 
• ارتفاع یک گره (Height of a Node):  به تعداد یال‌های گره تا آخرین برگ (عمیق‌ترین گره) درخت اشاره دارد. 
• ریشه (Root): بالاترین گره است.
• عمق گره (Depth of a Node): تعداد لبه‌ها از ریشه تا گره است.
• درجه (Degree): به تعداد کل شاخه‌های یک گره اشاره دارد. 
• جنگل (Forest): مجموعه‌ای از درختان ناهمگون است.

انواع ساختار‌های داده درختی

ساختار‌های داده درختی انواع مختلفی دارند، اما برخی از آن‌ها شناخته شده‌تر و پرکاربردتر هستند. این درختان به شرح زیر هستند:

1. درخت دودویی (Binary Tree)
2. درخت جست‌وجوی دودویی (Binary Search Tree)
3. درخت AVL
4. درخت بی (B-Tree)

پیمایش درخت

برای انجام هر عملیاتی روی یک گره، باید مسیری در درخت را انتخاب کنیم تا به گره مورد نیاز برسیم. در ساختار داده خطی، به دلیل خطی بودن توالی‌ها، پیمایش از جلو یا عقب ساده است. در ساختار داده‌های غیر خطی راه‌های مختلفی برای رسیدن به یک گره داریم. برای یافتن کوچک‌ترین گره در درخت، باید از تمام گره‌های درخت عبور کنیم، اما تکنیک‌های جست‌وجوی پیشرفته‌ای برای کوتا‌ه‌تر کردن زمان رسیدن به یک گره در اختیار ما قرار دارد. 

به طور کلی درخت از ریشه و سپس به سمت چپ و سپس به فرزند راست عبور می‌کند. نکته مهمی که باید به آن دقت کنید، این است که برای پیمایش درخت مجبور به استفاده از یک روش مشخص نیستید و در صورت نیاز، می‌توانید از پایین به بالا یا از بالا به پایین یا انتخاب گره‌ای به شکل تصادفی پیمایش را آغاز کنید تا به گره مقصد برسید. با این حال، پیمایش تصادفی هیچ‌گاه بهترین عملکرد را ارائه نمی‌کند و بهتر است به سراغ این روش نروید. مجموعه تکنیک‌هایی که برای پیمایش درختان در دسترس ما قرار دارند، به شرح زیر هستند:

هنگامی که قصد پیمایش یک درخت را دارید، پیشنهاد می‌کنیم به نکات زیر دقت کنید: 

1. هر گره باید داده‌ای داشته باشد.
2. هر گره ممکن است فرزند چپ و راست داشته باشد.

ما هر گره با فرزند را به عنوان درخت فرعی در نظر می‌گیریم، زیرا این گره‌های فرزند می‌توانند گره‌های فرعی بیشتری داشته باشند. شکل زیر این مسئله را نشان می‌دهد.

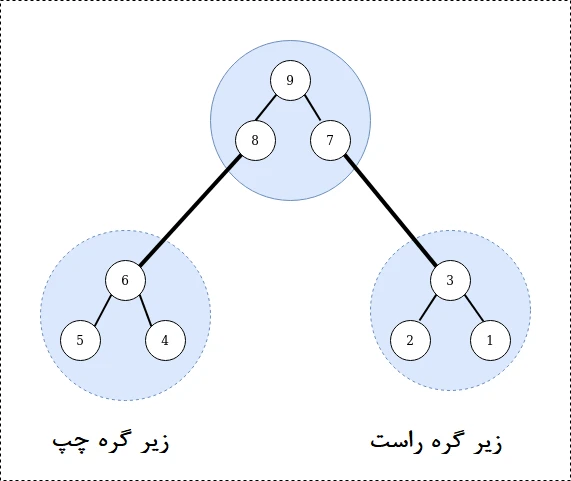
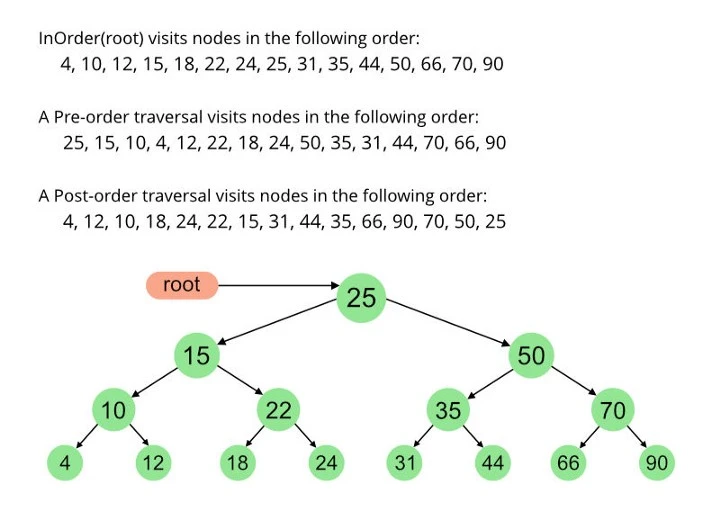
اگر هدف تنها پیمایش کل درخت است، بهتر است، از زیر درخت چپ، گره ریشه و زیر درخت سمت راست کار را آغاز کنیم. بسته به ترتیب پیمایش ما سه تکنیک پیمایش Inorder، Pre-Order و Post-order را در اختیار داریم.

پیمایش Inorder :

روش پیمایش درخت بر مبنای تکنیک فوق به این صورت است که ابتدا تمام گره‌های زیر درخت سمت چپ بازدید می‌شوند، در ادامه به سراغ  گره ریشه می‌رویم و در نهایت تمام گره‌های زیر درخت سمت راست را پیمایش می‌کنیم. 

پیمایش Pre-Order :

در روش فوق، پیمایش از گره ریشه آغاز می‌شود، در ادامه تمام گره‌های زیر درخت سمت چپ پیمایش می‌شوند و در نهایت، تمام گره‌های زیر درخت سمت راست پیمایش می‌شوند. 

پیمایش Post-Order

در روش فوق، ابتدا تمام گره‌های زیر درخت سمت چپ پیمایش می‌شوند، در ادامه به سراغ تمام گره‌های زیر درخت سمت راست می‌رویم و در نهایت به سراغ گره ریشه می‌رویم. 

پیاده‌سازی روش‌های پیمایش درخت 

اکنون که اطلاعات کلی در ارتباط با درخت‌ها و نحوه پیمایش آن‌ها به دست آوردیم، وقت آن رسیده تا به سراغ کدنویسی عملی سه تکنیک فوق برویم. در قطعه کد زیر، ما سه تابع تعریف کرده‌ایم که هر یک نحوه پیمایش یک درخت به شیوه Inorder، Post-Order و Pre-Order را نشان می‌دهند. برای آزمایش کدهای نشان داده شده، کافی است محیط توسعه یکپارچه (IDE) پایتون را باز کنید، فایل جدیدی ایجاد کنید، کدهای زیر را درون آن درج کنید، فایل را ذخیره کرده و گزینه Run Module از منوی اصلی محیط توسعه را انتخاب کنید تا کدها اجرا شوند. 

class Node:

    def __init__(self, data):

        self.left = None
        self.right = None
        self.data = data

# Insert method to create nodes
    def insert(self, data):

        if self.data:
            if data < self.data:
                if self.left is None:
                   self.left = Node(data)
               else:
                   self.left.insert(data)
            elif data > self.data:
                if self.right is None:
                    self.right = Node(data)
               else:
                   self.right.insert(data)
        else:
           self.data = data
# findval method to compare the value with nodes

    def findval(self, lkpval):
        if lkpval < self.data:
            if self.left is None:
               return str(lkpval)+" is not Found"
            return self.left.findval(lkpval)
        elif lkpval > self.data:
            if self.right is None:
               return str(lkpval)+" is not Found"
            return self.right.findval(lkpval)
        else:
            return str(self.data) + " is found"
# Print the tree

    def PrintTree(self):
        if self.left:
           self.left.PrintTree()
       print(self.data),
        if self.right:
           self.right.PrintTree()

root = Node(27)
root.insert(14)
root.insert(35)
root.insert(31)
root.insert(10)
root.insert(19)
print()
print(root.findval(7))
print(root.findval(14))

خروجی قطعه کد فوق، در شکل زیر نشان داده شده است. 

در برنامه بالا از تکنیک پر کاربرد بازگشتی استفاده کردیم. نکته‌ای که باید به آن دقت کنید این است که هنگام فراخوانی توابع به شیوه بازگشتی، تابع و زمینه اجرایی (Execution Context) آن در پشته ذخیره می‌شود و پس از کامل شدن فرآیند از پشته حذف می شود. 

لازم به توضیح است که زمینه اجرایی شامل کد در حال اجرا و هرگونه وابستگی (Dependency) مرتبط با کد است. در مدت زمان اجرا، کد توسط یک تجزیه‌کننده (Parser)، تجزیه می‌شود، متغیرها و توابع در حافظه ذخیره می‌شوند، کد بایت اجرایی تولید می‌شود و کد اجرا می‌شود. 

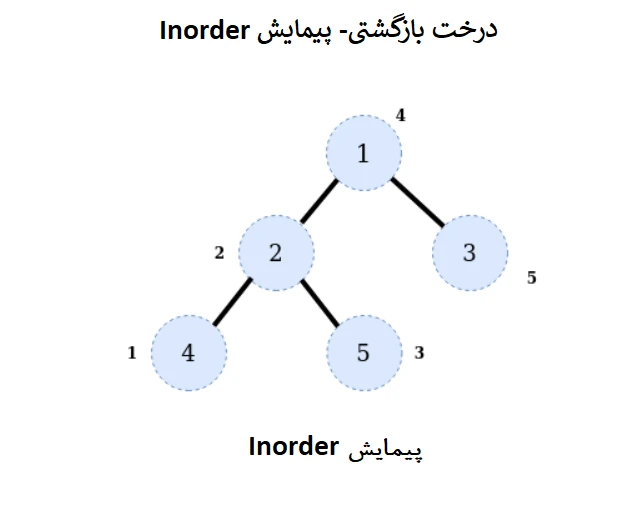
1. برای پیمایش به ترتیب، ابتدا درخت کامل را به تابع in-order منتقل می‌کنیم.
2. در ادامه، بررسی می‌کنیم که آیا شرط درست است یا خیر؟ از آن‌جایی که درخت خالی نیست، در صورت وجود بلوک‌ها فرآیند پیمایش به داخل درخت را آغاز می‌کنیم.
3. در مرحله بعد، ما با فرزند چپ ریشه به شیوه بازگشتی ارتباط برقرار می‌کنیم (گره 2، اینجا)، دوباره یک فرخوانی بازگشتی روی فرزند چپ گره 2 که گره 4 است، انجام می‌دهیم
4. در ادامه، شرایط را با فرزند چپ گره 4 بررسی می‌کنیم و فراخوانی بازگشتی را انجام می‌دهیم. 
5. اکنون، مقدار 4 چاپ می‌شود و سپس فرزند سمت راست گره 4 را برای برقرار بودن شرایط بررسی می‌کنیم. با توجه به این که هیچ فرزند سمت راستی برای گره 4 وجود ندارد، کار را خاتمه می‌دهیم.
6. در ادامه، مقدار 2 چاپ می‌شود، سپس فرزند سمت راست گره 2 برای احراز شرط بررسی می‌شود. در این جا فرزندی که گره 5 است، وجود دارد دوباره فراخوانی بازگشتی را انجام می‌دهیم. 
7. به همین ترتیب از چپ به راست پیمایش را انجام می‌دهیم تا به آخرین گره سمت راست 3 برسیم.
8. شرط پایه بازگشتی محقق نمی‌شود تا زمانی که همه گره‌ها پیمایش شوند، اگر شرط root: False باشد، به این معنی است که همه گره‌ها پیمایش شده‌اند و دیگر چیزی باقی نمانده است.

چرا از درخت‌ها استفاده می‌کنیم؟

درخت‌ها، به دلایل مختلفی مورد استفاده قرار می‌گیرند و برخی از برنامه‌های کاربردی را تنها با استفاده از درخت‌ها می‌توان پیاده‌سازی کرد. به طور مثال، بازی شطرنج از جمله، کاربردهای واقعی درخت‌ها است که امکان پیاده‌سازی آن بدون وجود درخت‌ها وجود ندارد، زیرا در زمان کوتاهی با مشکل کمبود حافظه اصلی روبرو می‌شویم. از کاربردهای مهم درخت‌ها به موارد زیر باید اشاره کرد:

• اگر کلیدها را به شکل درختی سازمان‌دهی کنیم (به ترتیب و مرتب شده)، می‌توانیم یک کلید معین را در بازه زمانی کوتاهی ​​(سریع‌تر از لیست‌های پیوندی کار می‌کند) جست‌وجو کرده و پیدا کنیم. درختان جست‌وجوی خودتعادلی (self-balancing) مانند AVL مخفف Adelson-Velsky Landis و درختان قرمز-مشکی پیچیدگی زمان کمتری دارند و تضمین می‌کنند، جست‌وجو با بالاترین سرعت انجام می‌شود. 
• می‌توانیم کلیدها را در زمان متوسطی (سریع‌تر از آرایه‌ها) درج یا حذف کنیم. درخت‌های جست‌وجوی خودتعادلی مانند AVL و درخت‌های قرمز-مشکی در هنگام انجام عملیات درج یا حذف پیچیدگی زمان کمتری دارند. 
• مانند لیست‌های پیوندی و برخلاف آرایه‌ها، محدودیتی در ارتباط با تعریف اشاره‌گرها و گره‌ها در درخت‌ها وجود ندارد، زیرا گره‌ها با استفاده از اشاره‌گر به هم متصل می‌شوند.
• درخت‌ها، اجازه می‌دهند، داده‌های دارای ساختار سلسله مراتبی مثل پوشه، ساختارهای سازمانی، داده‌های XML/HTML را به بهترین شکل ذخیره کنیم.
• هیپ (Heap)، یک ساختار داده درختی است که با استفاده از آرایه‌ها پیاده‌سازی شده و برای پیاده‌سازی صف‌های دارای اولویت استفاده می‌شود.
• B-Tree و B+ Tree، درخت‌هایی هستند که برای تعریف شاخص‌گذاری (indexing) در پایگاه های داده استفاده می‌شوند.
• درخت نحو (Syntax Tree): درختی است که فرآیند اسکن، تجزیه، ساخت کد و ارزیابی عبارات حسابی مورد استفاده در طراحی کامپایلرها را ساده می‌کند.
• درخت K-D: درخت تقسیم‌بندی (partitioning) فضا است که برای سازماندهی نقاط در فضای K بعدی استفاده می شود.
• Trie : گزینه مناسبی برای ساخت برنامه‌های فرهنگ لغت با جست‌وجوی پیشوندی (prefix lookup) است. 
• درخت Suffix Tree: درختی است که با هدف جست‌وجوی سریع الگو‌ها در یک متن ثابت مورد استفاده قرار می‌گیرد.
• درخت‌های پوشا و درخت‌های کوتاه‌ترین مسیر (Spanning Trees and shortest path): به ترتیب در روترها و بریج‌ها در شبکه‌های کامپیوتری استفاده می‌شوند.
• به عنوان راهکاری موثر در زمینه ترکیب تصاویر دیجیتال در ارتباط با جلوه‌های بصری مورد استفاده قرار می‌گیرند.
• از دیگر کاربردهای درخت‌ها باید به تعریف چارت‌های سازمانی بزرگ، تجزیه کننده XML، الگوریتم‌های یادگیری ماشین، نمایه‌سازی پایگاه داده‌های سرور IN شبیه به سرور سامانه نام دامنه (DNS)، گرافیک کامپیوتری، ارزیابی یک عبارت، در بازی شطرنج برای ذخیره‌سازی حرکات بازیکن و ماشین مجازی جاوا اشاره کرد.