مقایسه کامل روش های طراحی پایگاه داده سلسله مراتبی

مدل پایگاه داده سلسله مراتبی مدلی است که در آن داده ها در یک ساختار درخت مانند سازماندهی می شوند. در این پایگاه داده، داده ها به صورت پرونده هایی که از طریق یک لینک به یکدیگر متصل هستند، ذخیره می شوند. در این مدل هر رکورد فرزند فقط یک والد می تواند داشته باشد و نه بیشتر، در حالی که هر رکورد والد می تواند یک یا چند فرزند داشته باشد. در این روش تعدد والدین مجاز نیست که همین امر اصلی ترین تفاوت میان مدل سلسله مراتبی و مدل پایگاه داده شبکه ای (network database model) است.

به منظور بازیابی داده ها از یک پایگاه داده سلسله مراتبی، کل درخت را باید با شروع از گره ریشه، طی کرد. این مدل به عنوان اولین مدل بانک اطلاعاتی ایجاد شده توسط IBM در دهه 1960 شناخته شده است. این مدل در واقع نحوه کار سیستم های پرونده ای (file systems) را نمایش می دهد که به طور معمول یک پوشه root یا سطح بالا وجود دارد که شامل پوشه ها و فایل های مختلف دیگری هست. همچنین هر زیرشاخه می تواند حاوی فایل ها و پوشه های بیشتری باشد. باید توجه کرد که در این ساختار هر فایل یا پوشه فقط در یک پوشه وجود داشته و فقط یک والد دارد.

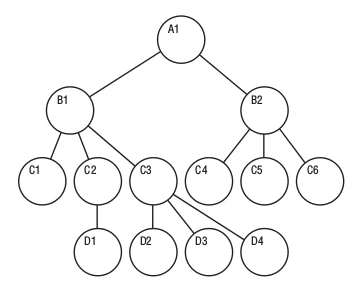
برای مثال همانطور که در شکل 1 مشخص است A1 فهرست اصلی یا root این مجموعه است که فرزندان آن B1 و B2 هستند. همینطور B1 به عنوان والد برای عناصر C1، C2 و C3 است و...

معایب کار با ساختار داده ای سلسله مراتبی

1. در این ساختار دسترسی به عناصر در سطح های پایینی درخت می تواند مشکل ساز باشد.
2. این ساختار حین نمایش روابط یک به چند ( برای مثال یک پوشه شامل چندین فایل است) عملکرد خوبی دارد اما در روابط چند به چند ( برای مثال یک پوشه شامل چندین پوشه (فرزند) دیگر است که هر کدام از پوشه ها خود شامل پوشه ها و فایل های دیگری است) با کندی روبرو می شود.
3. اضافه کردن، حذف و به روز رسانی یک عنصر نیازمند تغییر در کل ساختار است

روش های کار با ساختار داده ای سلسله مراتبی

4 روش از روش های کار با ساختار داده ای سلسله مراتبی را در قالب یک مثال (شکل 2) توضیح خواهیم داد. همچنین در پایان هر روش اشاره ای به مزایا و معایب هر کدام خواهیم کرد.

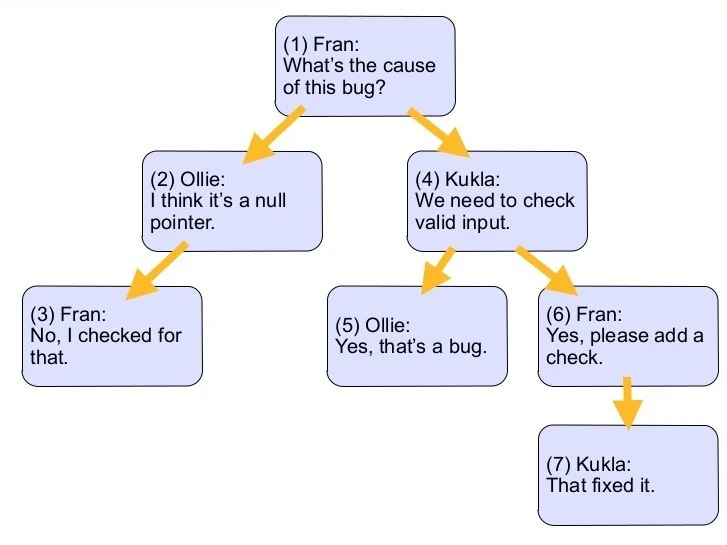
این روش ها عبارتند از:

• Adjacency List
• Nested Sets
• Path Enumeration (Lineage Column)
• Closure Table(Bridge Table)

💎 قبل از آنکه به ادامه‌ی مطالعه برای درک این 4 روش بپردازید؛ پیشنهاد می‌کنیم مروری بر مقاله‌ی اشتباهات رایج در طراحی دیتابیس داشته باشید.

روش Adjacency list

احتمالا همه شما با این روش آشنایی داشته باشید! این روش ابتدایی ترین راه، برای ذخیره داده های سلسله مراتبی است که با در نظر گرفتن یک فیلد با نام parent_id در جدول مورد نظرتان، می توانید والد سطر مورد نظرتان را مشخص کنید. در واقع در این روش هر سطر از جدول حین ساخته شدن، والد خودش را شناخته یا به عبارت دیگر با مراجعه به هر رکورد، می توان بلافاصله نام رکورد والد آن را پیدا کرد.

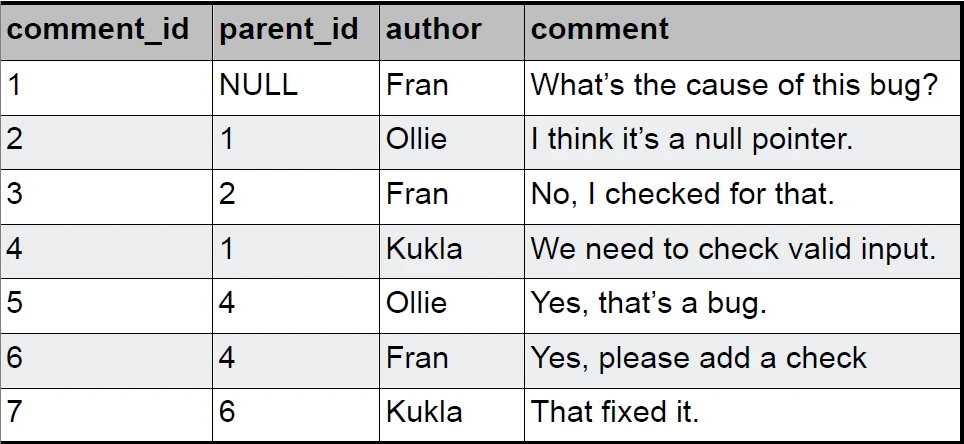
مزایای روش Adjacency list:

1. پیاده سازی راحت و ساده ای دارد.
2. عملیات ذخیره، هرس (حذف یک نود به همراه کلیه فرزندان و نوادگانش) و به روز رسانی در این روش دارای مرتبه زمانی o(n) است. 
   ** مقصود از نود در اینجا یک کامنت است.
3. به دلیل وجود parent_id، واکشی فرزندان اولین سطح از هر نود کاری ساده بوده و برای انجام این کار کوئری های join نیاز است.
4. یکپارچگی مرجع دارد یا به عبارتی Referential integrity است.
   ** مقصود از یکپارچگی مرجع یعنی در جداولی که باهم در ارتباط هستند باید بتوان از طریق کلید خارجی به کلید اصلی آن راه پیدا کرد (و برعکس) و در صورت هر گونه تغییری در کلید اصلی بایستی این تغییر بر روی تمامی کلیدهای خارجی اعمال شود.

معایب روش Adjacency list:

نیازمند کوئری های بازگشتی (تعداد join های بالا) برای دسترسی به نوادگان یک نود است.

نکته: احتمالا فکر کنید که می توان بدون کوئری های بازگشتی نتیجه درخواستی را نمایش داد، بدین صورت که با گرفتن قسمتی از داده هایی که در نظر داریم و صدا زدن تابع های بازگشتی، مشکل را برطرف کنیم اما در واقع خود همین کار به شدت منابع سیستم را درگیر کرده و در داده های با حجم بالا این موضوع مشکل ساز خواهد شد!

روش Nested Sets

این روش، شماره گذاری گره ها بر اساس پیمایش درخت است. بدین صورت که با شروع از گره اصلی، هر گره دو بار در طول مسیر بازدید می -شود و شماره گذاری ها به ترتیب بازدید انجام می شوند. در نهایت با اتمام شماره گذاری، بایستی برای هر گره دو عدد باقی مانده باشد که به عنوان دو صفت در جدول مورد نظرمان ذخیره می شوند. این دو عدد (left & right) در واقع مشخص کننده رابطه میان فرزندان و والد در ساختار داده ای است که در ادامه به چگونگی ارتباط این دو عدد و نحوه عملکردشان خواهیم پرداخت. 

با توضیحات داده شده در خصوص نحوه شماره گذاری نودها در شکل 1-2 در این روش، در نهایت به شکل 2-2 خواهیم رسید.
 

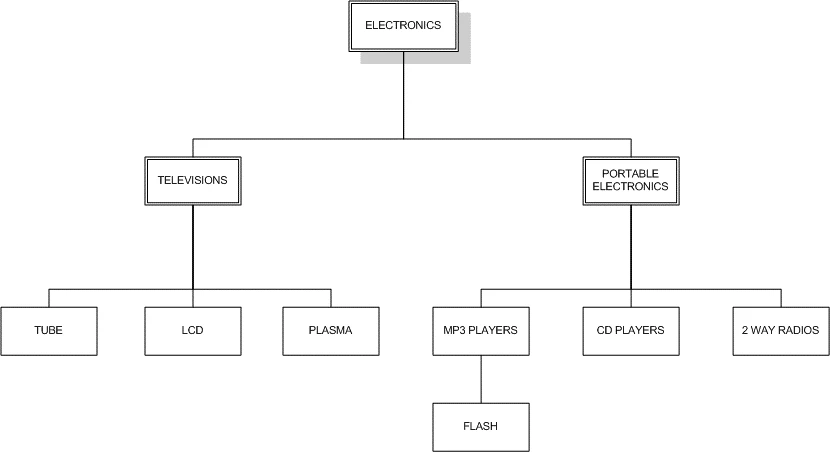
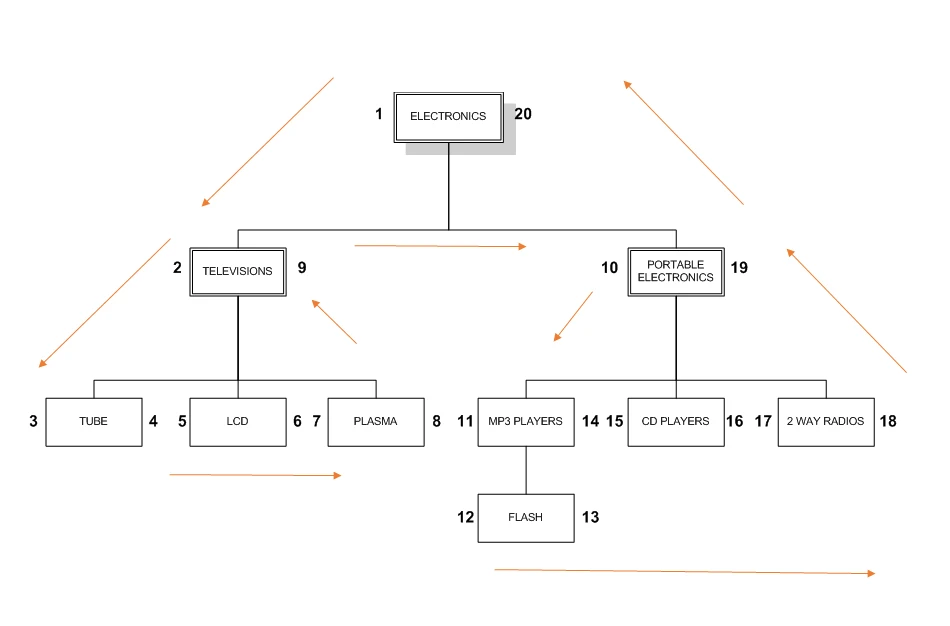
همان طور که در شکل 2-2 ملاحظه می کنید شماره گذاری به صورت صعودی از سمت چپ شروع شده و تا رسیدن به نود اصلی این کار ادامه داشته است. برای درک بهتر سناریو ذخیره شدن یک عنصر در این روش، فرض کنید قصد ذخیره داده ی electronics را با توجه به شکل 2-2، داریم:
مقدار سمت چپ داده electronics یعنی مقدار 1 می شود فرزند چپ و مقدار سمت راست آن، یعنی 20 می شود فرزند سمت راست. به همین ترتیب برای televisions فرزند چپ مقدار 2 و فرزند راست مقدار 9 را به خودش اختصاص می دهد.
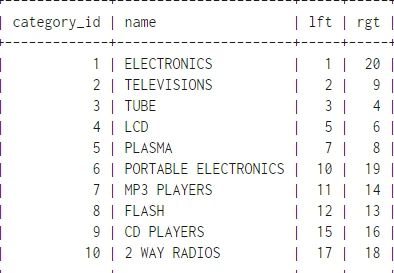
در نهایت رکوردهای جدول مربوط به دسته بندی الکترونیکی به صورت زیر خواهد شد:

بعد از شماره گذاری عناصر می توان نکات زیر را از درخت به دست آمده در شکل 2-2 استخراج کرد: 

1. مقادیری که فرزندی ندارند مقدار فیلدهای left & right برای آن ها، دو عدد ترتیبی پشت سر هم از کوچک به بزرگ هستند.
2. همیشه مقدار child_left > parent_left است.
3. همیشه مقدار child_right < parent_right است.

اگر نکات به دست آمده از شکل 3-2 را بررسی کنیم خواهیم دید که تمامی این نکات در مثال دسته بندی الکترونیکی صدق می کنند!
برای مثال LCD به عنوان داده ای که هیچ زیر مجموعه ای ندارد، مقدار فرزندان چپ و راستش به صورت 5 و 6 (ترتیبی) هستند. همچنین با توجه به اینکه LCD زیر مجموعه ای از Television است مقدار فرزند چپش یعنی 5 از مقدار فرزند چپ والد خود یعنی 2 بیشتر و مقدار سمت راست آن یعنی 6 از مقدار فرزند راست پدر خود یعنی 9 کمتر است.
حال به مثال خودمان یعنی کامنت ها می پردازیم:
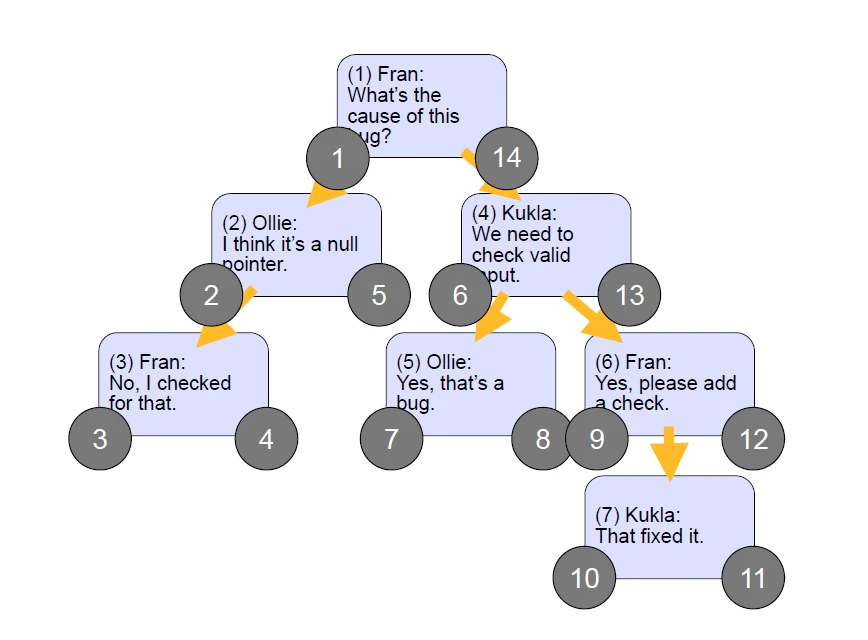
طبق روشی که در مثال بالا توضیح داده شد مقادیر left & right برای کامنت ها به شکل 4-2 خواهد شد:

و بعد از مشخص شدن مقادیر left & right می توانیم رکوردهای جدول کامنت را ایجاد کنیم.

نکته ها:

1. با استفاده از فرمول زیر می توانید به راحتی تعداد کلیه فرزندان و نوادگان هر نود را به دست بیاورید.

  2/( 1–(right – left) ) = تعداد کلیه فرزندان و نوادگان یک نود

برای مثال کامنت 4 را در نظر بگیرید:

2/(13-6-1)=3

که با توجه به شکل 4-2 تعداد کلیه فرزندان و نوادگان کامنت 4 برابر 3 است.
2. به صورت اختیاری می توان فیلدی را به عنوان level یا depth برای این جدول در نظر گرفت که در واقع نشان دهنده عمق درخت در هر سطح است. همچنین با استفاده از این فیلد می توان کوئری های هدفمندتری برای واکشی داده ها انجام داد ( برای مثال به جای گرفتن تمامی فرزندان یک نود، صرفا به اندازه یک عمق مشخص، این کار انجام شود).

در ادامه چند مثال از نحوه واکشی اطلاعات در این روش را توضیح خواهیم داد: 

مثال 1: واکشی کلیه فرزندان کامنت 4 به همراه خودش

SELECT node.*
FROM comments as node
    INNER JOIN comments as parent ON
    (node.nsleft >= parent.nsleft AND node.nsleft <= parent.nsright)
WHERE
    parent.auther = "Kukla"
ORDER BY node.nsleft;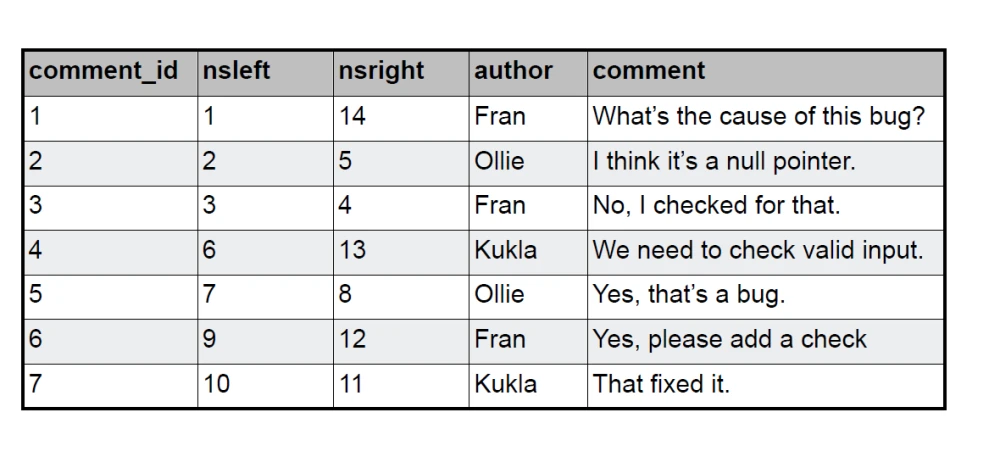

مثال 2: واکشی اجداد کامنت 6 به همراه خودش

SELECT parent.*
FROM comments as node
    INNER JOIN comments as parent ON
   ( parent.nsleft <= node.nsleft AND parent.nsright >= node.nsleft )
WHERE
    node.auther = "Fran"
ORDER BY node.nsleft;

شکل 7-2 واکشی کلیه اجداد کامنت با آیدی 6

مزایای روش Nested Sets:

1. نمایش و دسترسی به نقاط یک شاخه یا برگ های یک درخت، کاری ساده و با کوئری های ساده قابل حصول است
**منظور این هست که واکشی فرزندان یک نود یا اجدادش، نیازمند تعداد join های بالا و بازگشتی نیست و تنها با یک join می توان این کار را انجام داد. (مثال های 1 و 2)
2. مناسب برای ساختارهای داده ای جنگل (ساختارهایی که از عمق زیادی برخوردار نیستند)!

معایب روش Nested Sets:

1. پیچیدگی در پیاده سازی دارد.
2. برای دسترسی به پدر یا فرزند یک نود، کوئری پیچیده ای نیاز است.
3. نیازمند کوئری های زیاد و پیچیده برای حذف یا اضافه کردن یک مقدار جدید است.
4. یکپارچگی مرجع ندارد. (چون از کلید خارجی در این جدول استفاده نشده است!)

توضیح مورد 2: فرض کنید پدر کامنت با آیدی 6 را می خواهید! خب به نظرتان با داشتن کامنت 6 چگونه می توان به کامنت با آیدی 5 رسید؟ با کمی تفکر انجام این کار شدنی است اما نیازمند کوئری پیچیده ای است!
توضیح مورد 3: چون این سیستم بر پایه مقادیر فرزندان چپ و راست عمل می کند با اضافه شدن یک مقدار جدید بایستی تمامی مقادیر فرزندان چپ و راست در کل درخت به روز رسانی شوند، در نتیجه این عملیات هزینه زیادی را به ما تحمیل می کند.

روش Path Enumeration

این روش مشابه روش شماره 1 است. با این تفاوت که بجای فیلد parent_id فیلد path را داریم که در آن id تمامی parent ها نوشته شده و با کاراکتری غیرعددی مانند اسلش (/) یا نقطه (.) از هم جدا می شوند.
در این روش آیدی تمامی parentها در صورت وجود به صورت زنجیره وار (صعودی) در هر رکورد ذخیره می شوند.
اگر مثال کامنت را با استفاده از این روش مدل کنیم جدول حاصل شده از این روش به شکل 1-3 خواهد بود:

شاید برایتان این سوال ایجاد شود که چرا در فیلد path در انتهای هر مقداری/ گذاشته شده است؟

اینکار را برای جلوگیری از جستجوهای اشتباه احتمالی انجام می دهیم. فرض کنید path دیگری را با مقدار 40/1 داریم. اگر / آخری وجود نداشته باشد، برای واکشی فرزندان کامنت 4 با استفاده از عملگر like، علاوه بر فرزندان کامنت 4 فرزندان کامنت 40 هم در صورت وجود، برای ما برگشت داده می شود که مقادیر برگشتی با چیزی که انتظار می رود متفاوت خواهد بود!

نکته: می توانید فیلد دیگری را با عنوان parent_id برای جدول خود در نظر بگیرید که این فیلد همانند روش اول، در واقع مشخص کننده والد هر رکورد است و می تواند در برخی از کوئری ها کمکمان کند. (برای مثال در حین انتقال یک شاخه به شاخه دیگر می توانیم به جای استفاده از path از مقدار parent_id برای دسترسی به تمامی رکوردهایی که قصد جابجایی شان را داریم، استفاده کنیم که در این حالت کوئری با سرعت بیشتری انجام می شود)!
** برای اطلاعات بیشتر می توانید در خصوص مقایسه سرعت اجرای دستور SELECT با نوع داده ای int & varchar تحقیق کنید.

اگر سناریو ذخیره شدن کامنت سوم را بخواهیم تجسم کنیم به این صورت خواهد شد:

درخواست ثبت یک بازخورد برای کامنت با آیدی 2 ارسال می شود. در ابتدا درخواست ارسال شده به همراه اطلاعات موجود در جدول مربوطه بدون داشتن مقدار path ذخیره می شود. بعد از ذخیره شدن، کوئری برای پیدا شدن کامنت با آیدی 2 زده می شود و بعد از پیدا شدن، مقدار path آن گرفته شده و در انتهای آن آیدی بازخورد (کامنت جدید) اضافه می شود و در نهایت مقدار فیلد path، برای کامنت ثبت شده به روزرسانی می شود.
چند مثال از نحوه کوئری زدن روی این جدول را باهم ببینیم:

مثال 1 (SELECT کردن): تمامی فرزندان و نوادگان کامنت 4 رو، برگردان.

SELECT * FROM comments WHERE path LIKE '1/4/%' ORDER BY path ASC;

مثال 2 (DELETE کردن): برای حذف هم دقیقا سناریو select کردن را داریم.

DELETE FROM comments WHERE path LIKE '/1/4/%';

مزایای روش Path Enumeration:

1. سادگی در مدل کردن روش(پیاده سازی)
2. مناسب برای درختان پهن با عمق کم(به صورت خلاصه می توان گفت مناسب برای مجموعه داده های با حجم کم یا متوسط)
3. سادگی در حین درج اطلاعات جدید
4. سادگی در حین انتقال یک شاخه به شاخه دیگر
   ** برای مثال فرض کنید قصد عوض کردن پدر کامنت 4، به کامنت 2 را دارید! کافیست تمامی رکوردهایی که شامل path با مقدار 1/4 می شوند را پیدا کرده و جای 1 مقدار 2 رو قرار بدهید!
5. در حجم داده ای متوسط، دسترسی آسان به نوادگان یک نود 
   ** چون تمامی کوئری ها بر روی نوع داده ای string اعمال می شود (در این نوع داده، مشکل index کردن به وجود می آید)، در صورتی که حجم داده ای بزرگی داشته باشیم با کندی قابل توجهی، نتیجه کوئری مورد نظرمان برگشت داده خواهد شد.

معایب روش Path Enumeration:

1. پیچیدگی و تغییرات زیاد حین اضافه کردن و به روزرسانی رکورد های موجود
2. انجام 2 عملیات حین درج رکورد جدید در جدول مربوطه
3. عملیات پیچیده برای دسترسی به فرزندان یک نود
4.نبود یکپارچگی مرجع در صورت نداشتن فیلد parent_id ( در روش اول توضیح داده شده)
نکته: این روش در دیتابیس های Nosql مانند MongoDB (به دلیل رفتاری که با داده های ایندکس نشده دارد) عملکرد بهتری دارد!

روش Closure Table

این روش در واقع نرمال شده روش path enumeration است! در این روش دو جدول داریم که یکی از جداول برای ذخیره داده ها و جدول دوم برای ذخیره تمامی مسیرهای (ارتباطات) بین دو نقطه (با شروع از نود اصلی) است. رابطه این دو جدول باید many-to-many باشد.
برای درک بهتر این روش به گونه دیگری به توضیح این روش می پردازیم و سپس مثالی را در رابطه با آن توضیح می دهیم:
در روش اول (adjacency list) با استفاده از فیلد parent_id، والد هر رکورد در صورت وجود مشخص می شود. در واقع تا یک سطح از روابط میان داده ها را می توانستیم با این روش شناسایی کنیم. حال اگر بخواهیم روابط میان داده ها را در هر عمقی بدون نیاز به کوئری های زمان بر داشته باشیم بایستی مسیرهای موجود میان آنها را از نود اصلی به تمامی نودهای دیگر در یک جدول دیگر ذخیره کنیم که در واقع این جدول نقش clouser table را برای ما ایفا می کند!
مثال:
فرض کنید A پدر B و Bپدر C و C پدر D است.
تمامی مسیرهایی که بایستی در جدول clouser ذخیره شوند به صورت زیر هستند:
A-A , A-B , A-C, A-D, B-B, B-C, B-D, C-C, C-D
خب با توجه به مسیرهای موجود به راحتی می توانید فرزندان و نوادگان A را در هر سطحی که می خواهید داشته باشید.

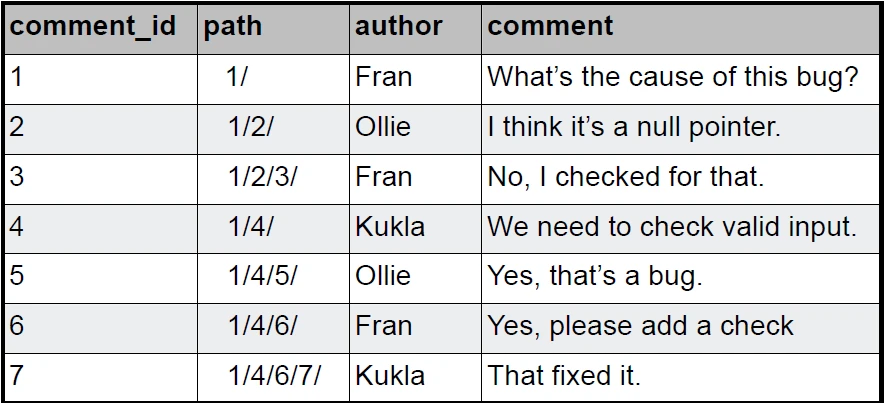
از معایب روش Closure Table می توان به ساخته شدن تعداد زیادی رکورد، درون جدول مسیرها اشاره کرد که در بدترین حالت (درخت کامل) تعداد (n^2) رکورد برای مسیرهایمان بایستی داشته باشیم.

در ادامه به توضیح مثال کامنت می پردازیم:

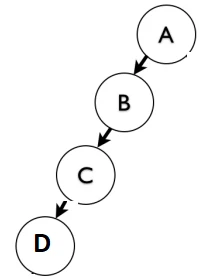
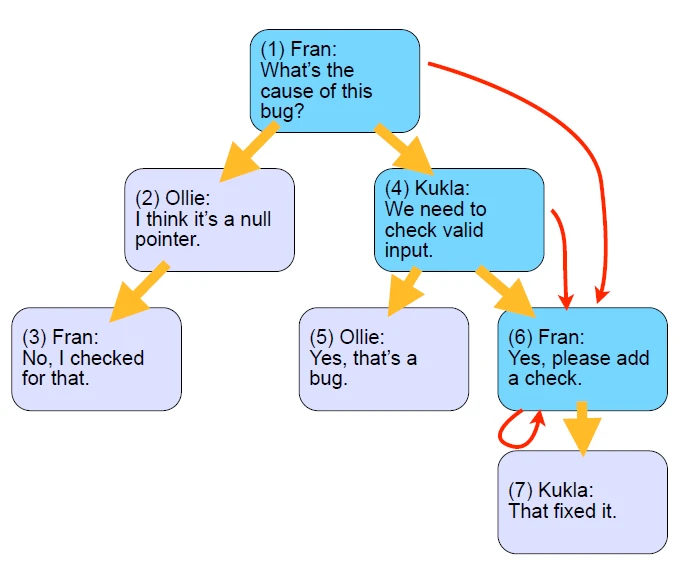
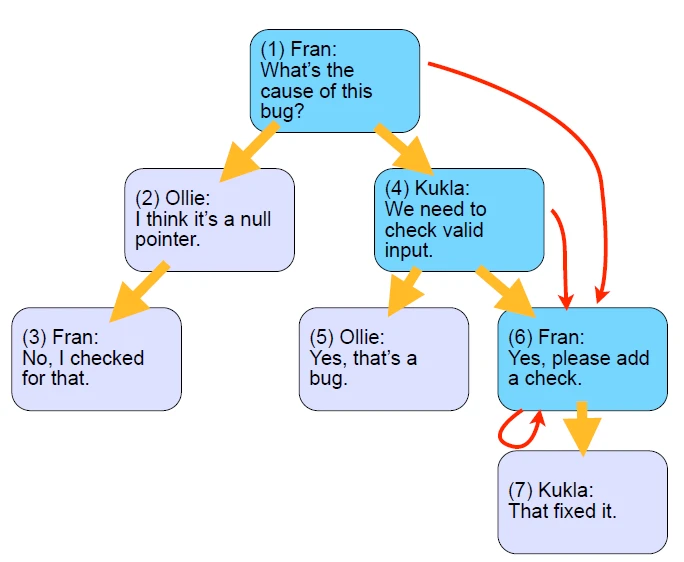
 هر کدام از فلش ها در شکل 1-4 به عنوان یک مسیر در نظر گرفته خواهد شد.

با توجه به توضیحات بالا در نهایت جداولمان به شکل های 2-4 و 3-4 خواهد شد:

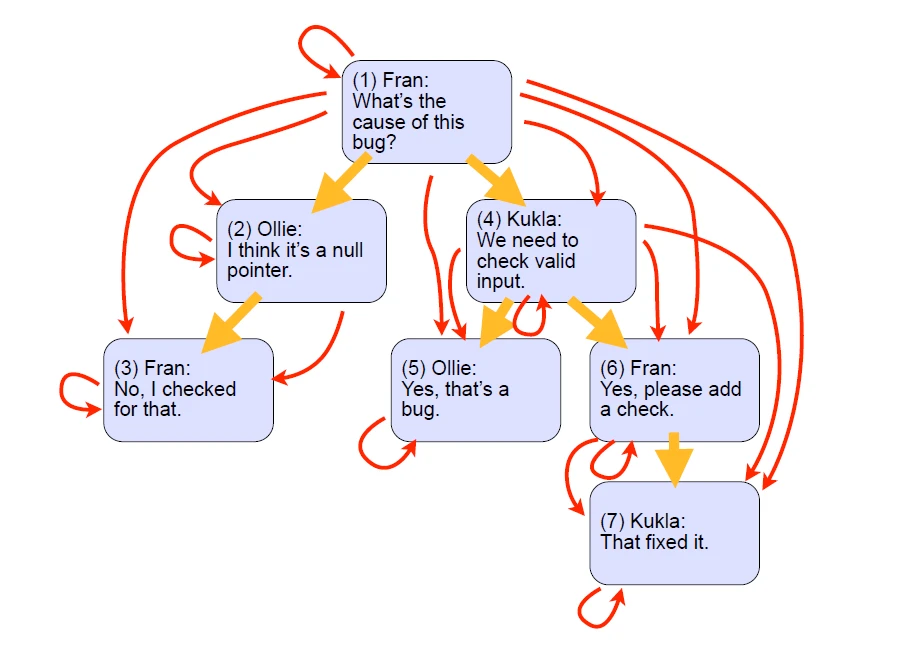
خب همان طور که پیش تر گفتیم یک جدول برای ذخیره اطلاعات و جدول دیگری برای ذخیره ارتباطلات میان داده ها، باید داشته باشیم.

در ادامه به بررسی مثال هایی از نحوه واکشی اطلاعات در این روش می پردازیم:

مثال 1: پیدا کردن فرزندان کامنت با آیدی 4

SELECT c.* FROM Comments c
JOIN TreePaths t
ON (c.comment_id = t.descendant)
WHERE t.ancestor = 4;

مثال 2: پیدا کردن اجداد کامنت با آیدی 6

SELECT c.* FROM Comments c
JOIN TreePaths t
ON (c.comment_id = t.ancestor)
WHERE t.descendant = 6;

مثال 3: اضافه کردن یک فرزند جدید برای کامنت با آیدی 5 
قبل از اینکه کوئری این مثال را توضیح دهیم در ابتدا در خصوص اتفاقی که بعد از اضافه شدن یک فرزند به کامنت مورد نظرمان رخ می دهد، توضیح می دهیم:
بعد از اضافه شدن یک فرزند بایستی به ازای تمامی نودهایی که با این فرزند در ارتباط هستند، مسیری در جدول clouser یا همان TreePaths ایجاد کنیم. برای انجام کار اینکار کافیست یک کپی از تمامی مسیرهایی که به کامنت 5 منتهی می شوند، بگیریم و بعد مقدار آیدی 5 را با آیدی کامنت جدید اضافه شده، تغییر بدهیم.
توضیحات داده شده را به صورت عملی پیاده می کنیم:

INSERT INTO Comments
VALUES (8, ‘Fran’, ‘I agree!’);

INSERT INTO TreePaths (ancestor, descendant)
SELECT ancestor, 8 FROM TreePaths
WHERE descendant = 5
UNION ALL SELECT 8, 8;

سوال: دلیل استفاده از UNION ALL در کوئری روبرو چیست؟

جواب: در واقع عمل کپی کردن مسیرها را دستور UNION ALL (ترکیب کردن تمامی SELECTها) اجرا می کند.
خب همانطور که پیش تر گفتیم بعد از ایجاد کامنت جدید (آیدی 8)، تمامی مسیرهایی که به کامنت والد (آیدی 5) منتهی می شوند، گرفته شده و به جای آیدی 5، آیدی کامنت جدید قرار می گیرد و در نهایت به جدول TreePaths اضافه می شوند.

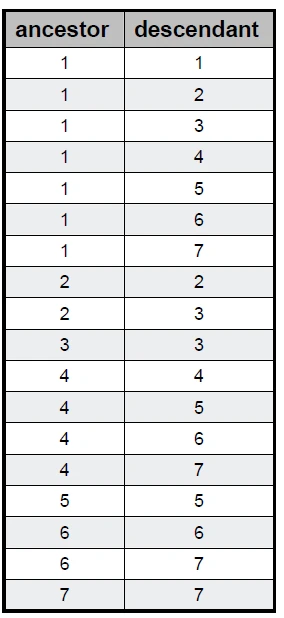
جدول مسیرها بعد از اضافه شدن کامنت جدید به شکل 6-4 خواهد شد:

مثال 4: حذف کردن کامنت با آیدی 4 به همراه تمام فرزندان و نوادگان

DELETE FROM TreePaths
WHERE descendant IN
(SELECT descendant FROM TreePaths
WHERE ancestor = 4);

نکته: برای راحتی کار و همچنین پی بردن به عمق سطحی که نودها قرار دارن معمولا فیلدی را به عنوان length برای جدول clouser در نظر می گیرند که مزایای این کار عبارت است از:
1. بیشترین مقدار length در واقع نشان دهنده عمق درخت است.
2. کوئری های جستجو را آسان تر می کند (فرض کنید فقط خواستار نوادگان یک کامنت در یک عمق به خصوصی است)

مزایای روش Closure Table:

عملیات مربوط به درج، حذف، به روزرسانی و استخراج داده ها بدون پیچیدگی خاصی قابل انجام شدن می باشند.
2. سادگی در مدل کردن روش( پیاده سازی ) وجود دارد.
3. به دلیل ذخیره تمامی مسیرهای موجود برای هر نود، این روش میتواند برای ساختار گراف ها مناسب باشد. (تعدد والدین در این ساختار وجود دارد).

معایب روش Closure Table:

1. نیاز به 2 جدول دارد
2. در صورتی که با داده های حجیم سلسله مراتبی سر و کار داشته باشید جدول clouser بسیار سنگین خواهد شد (همانطور که گفتیم در بدترین حالت n^2 رکورد).
3. به دلیل ذخیره تمامی مسیرهای موجود میان نودها، در بیشتر اوقات تعدادی از مسیرها بلااستفاده باقی می مانند.

حال می توان با در نظر گرفتن هر مفهوم، به مقایسه و یافتن بهترین الگوی طراحی پرداخت. و به سوال زیر پاسخ داد.

کدام الگوی طراحی برای کار با ساختار داده ای سلسله مراتبی بهتر است؟

Adjacency List: ساده ترین روش برای کار با ساختار داده ای سلسله مراتبی است و تقریبا اکثر توسعه دهندگان با آن آشنایی دارند. این روش به دلیل تعداد جوین های بالا برای واکشی اطلاعات در عمق های مختلف، بیشتر برای Write کردن مناسب است تا Read کردن اطلاعات.

Nested Sets: یکی از هوشمندانه ترین روش ها برای کار با این نوع ساختار داده ای است اما متاسفانه از یکپارچگی مرجع پشتیبانی نمی کند. این روش برای زمانی که عملیات خواندن داده بیشتر از نوشتن است، می تواند روش مناسبی باشد. 

Path Enumeration: این روش در واقع مشکل تعداد جوین های بالا برای دسترسی به اطلاعات در عمق های مختلف را برای روش adjacency list حل کرده است. میتواند برای داده های با حجم کم مناسب باشد اما در حجم داده ای بالا به دلیل کار با نوع داده ای string سرعت اجرای کوئری ها با افت قابل توجهی روبرو خواهد شد.

Closure Table: تنها روشی که از ذخیره داده های شبکه ای (یک فرزند شامل چند والد باشد) پشتیبانی کرده و همچنین تمامی عملیات CRUD (ساخت، خواندن، به روزرسانی، حذف) را بدون نیاز به کوئری های پیچیده انجام می دهد. این روش در حجم داده ای بالا به دلیل ذخیره مسیرهای زیاد و همچنین بلااستفاده که باعث ایجاد داده های هرز (spam) می شود، پیشنهاد نمی شود.

به نظرم در نظر گرفتن شرایط زیر می تواند در تصمیم گیری هرچه بهتر این روش ها موثر باشد: 

آینده داده هایتان را از لحاظ حجمی چگونه بررسی می کنید؟

چه عملیاتی را با چه نسبتی قرار است روی داده هایتان پیاده کنید؟ ( برای مثال واکشی داده هایتان بیشتر از ایجاد آن ها هستش یا برعکس) 

مقایسه روش های کار با ساختار داده ای سلسله مراتبی

** مقصود از Easy یا Hard در شکل، مشخص کردن سادگی یا پیچیدگی در عملیات مشخص شده است. 

  Query Child: عملیات مربوط به واکشی صرفا فرزندان یک نود(در یک سطح مشخص)

  Query Subtree: عملیات مربوط به واکشی تمامی فرزندان و نوادگان یک نود

ما در این مقاله به 4 روش از روش های کار با داده های سلسله مراتبی اشاره کردیم. روش های دیگری هم برای کار با این نوع ساختار داده ای وجود دارد اما نسبت به روش های گفته شده از محبوبیت کمتری برخوردار هستند که در صورت نیاز می توانید بیشتر راجع به آن ها تحقیق کنید.

• Flat Table
• Nested Intervals
• Multiple lineage columns

همانطور که گفتیم رویکردهای مختلفی در خصوص کار با ساختار داده ای سلسله مراتبی وجود دارد اما انتخاب روش درست بستگی به نوع سیستم شما، حجم داده ای و همچنین عملیات های مورد نظرتان دارد. چون این روش ها در حالت های مختلف رفتارهای متفاوتی را از خودشان نشان می دهند.

منابع:

https://www.gmarik.info/blog/2012/recursive-data-structures-with-rails

https://www.waitingforcode.com/mysql/managing-hierarchical-data-in-mysql-closure-table/read

https://www.technobytz.com/closure_table_store_hierarchical_data.html

https://www.percona.com/blog/2011/02/14/moving-subtrees-in-closure-table/

https://stackoverflow.com/questions/192220/what-is-the-most-efficient-elegant-way-to-parse-a-flat-table-into-a-tree

https://www.slideshare.net/billkarwin/models-for-hierarchical-data?from_action=save

https://www.codingblocks.net/podcast/episode-29-hierarchical-data-contd-path-enumeration-and-closure-tables/

https://bojanz.wordpress.com/2014/04/25/storing-hierarchical-data-materialized-path/

http://mikehillyer.com/articles/managing-hierarchical-data-in-mysql