RSA یک الگوریتم رمزگذاری است که برای انتقال ایمن پیام ها از طریق اینترنت استفاده می شود. این روش رمزگذاری، بر این اصل استوار است که ضرب اعداد بزرگ آسان است، اما فاکتورگیری از اعداد بزرگ بسیار دشوار است. به عنوان مثال، به راحتی می توان بررسی کرد که 31 و 37 در 1147 ضرب می شوند، اما تلاش برای یافتن فاکتورهای 1147 فرآیند بسیار طولانی تری است.
بررسی کلی
RSA نمونهای از رمزنگاری کلید عمومی است که با مثال زیر نشان داده میشود:
فرض کنید مینا میخواهد یک الماس ارزشمند برای شهرزاد بفرستد، اما اگر در ارسال الماس ها موارد ایمنی رعایت نشود، به سرقت خواهند رفت. مینا برای خودش قفلی دارد و شهرزاد هم قفل دیگری دارد و هر کدام از آنها هم کلیدی دارند که می تواند قفل دیگری را باز کند. حالا بیاید مسئله را با هم بررسی کنیم. موضوع این است که:
مینا می خواهد برای شهرزاد الماسی گران ارزشمند را ارسال کند. چطور این کار را انجام دهد که مورد سرقت قرار نگیرد؟
راه حل:
- شهرزاد، ابتدا یک قفل باز شده برای مینا می فرستد. توجه داشته باشید که شهرزاد به هر کسی یک قفل باز می دهد، زیرا تنها استفاده از آن این است که چیزی برای شهرزاد بفرستند.
- مینا ، قفل شهرزاد را روی بسته می زند و برای او میفرستد.
- شهرزاد قفل اش را باز می کند و بسته را باز می کند.
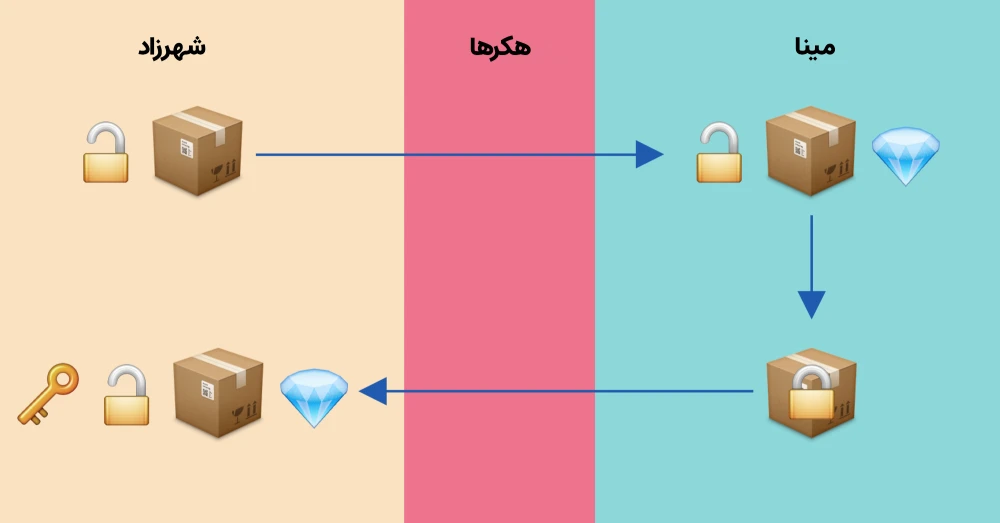
این مثال ایده های پشت رمزنگاری کلید عمومی را نشان می دهد، البته در واقع مفهوم کلید عمومی و خصوصی کمی متفاوت است. در رمزنگاری کلید عمومی مینا پیام خود را با استفاده از کلید عمومی شهرزاد رمزگذاری می کند، این پیام رمز شده، حالا فقط با کلید خصوصی شهرزاد قابل رمزگشایی است.
در RSA، کلید عمومی با ضرب دو عدد اول بزرگ p و q در یکدیگر تولید میشود و کلید خصوصی از طریق فرآیند متفاوتی که شامل p و q هست، تولید میشود. سپس کاربر می تواند کلید عمومی خود را که pq است به دیگران بدهد. حالا هرکسی که بخواهد برای کاربر پیامی ارسال کند، باید پیام خود را با استفاده از کلید عمومی رمزگذاری کند. حتی کامپیوترها هم نمیتوانند در فاکتورگیری از اعداد بزرگ برای بدست آوردن اعداد اول p و q موفق عمل کنند. به همان شکلی که فاکتورگیری عددی مانند 414863 با دست عملاً غیرممکن است.
وقتی کاربر، پیام رمزشده ای را دریافت می کند، با استفاده از کلید خصوصی خود، پیام را رمزگشایی کرده و آن را می خواند. در ادامه سعی می کنم همین موضوع را با جزئیات دقیق تر و البته فنی تر برایتان توضیح بدهم.
الگوریتم RSA
در پیاده سازی RSA از محاسبات Modular (هم نهشتی)، قضیه اویلر (Euler) و تابع فی اویلر به شدت استفاده شده است. توجه داشته باشید که هر مرحله از الگوریتم RSA فقط شامل ضرب است، بنابراین انجام آن برای کامپیوتر آسان است. این که کلید عمومی و خصوصی، دقیقا چطور ساخته می شوند، نیازمند توضیح ریاضی زیاد است که در این مقاله از آن چشم پوشی می کنیم. فقط به صورت کلی بدانید که کلید های خصوصی و عمومی، اعدادی هستند که برای رمزگذاری و رمزگشایی مورد استفاده قرار می گیرند. و هر کدام از آنها در با محاسبات ریاضی متعددی بدست می آیند.
بازیگران اصلی برای بدست آوردن کلید های خصوصی و عمومی مقادیر e ،n ،q ،p و d هستند که به طور مختصر در ادامه می گویم هر کدام از آنها چگونه و از کجا به دست می آیند.
همانطور که گفتیم p و q اعداد اولی هستند که به صورت تصادفی انتخاب می شوند و شرط انتخاب شدن شان هم این است که با هم برابر نباشند. سپس از ضرب این دو عدد در هم n بدست می آید. حال وقت آن است که e را تعیین کنیم این عدد معمولا معادل 2 به توان 16 است. برای عدد e کوچکترین مقداری که می توان انتخاب کرد عدد 3 است. هرچند که با انتخاب این عدد می توانیم رمزگذاری و رمزگشایی سریعتری داشته باشیم، ولی باعث کم شدن از امنیت رمز می شود. عدد d هم از فرمولی بر اساس e و n بدست می آید.
حالا که بازیگران اصلی مشخص شدند، کلید عمومی با استفاده از اعداد n (عدد مشترک بین کلیدخصوصی و عمومی) و e (عدد عمومی) و کلید خصوصی با استفاده از اعداد n و d (عدد خصوصی) بدست می آیند.
کاربردها و آسیب پذیری ها
به دلیل دشواری زیاد در شکستن RSA، تقریباً در هر جایی که نیاز به رمزگذاری باشد، مانند تبادل رمز عبور، بانکداری، خرید آنلاین و حتی تلویزیون کابلی از این الگوریتم رمزگذاری استفاده می شود. برای اطمینان از قانونی بودن وب سایت ها هم از RSA استفاده می شود. زیرا فقط وب سایت واقعی، کلید خصوصی خود را دارد. بنابراین از حمله های امنیتی Man-in-the-Middle به صورت موفقی جلوگیری می کند در حمله های Man-in-the-Middle، مهاجم یک اتصال را رهگیری می کند و تقریباً ارتباط بین کاربر و سایت را به صورت کاملا متقاعد کننده ای جعل می کند. در نتیجه، کاربر باور می کند اطلاعاتش را به سایت مورد نظر ارسال کرده و پاسخ های دریافت شده هم از سایتی است که انتظارش را داشته است. با توجه به موارد استفاده ی بسیار زیاد از این الگوریتم، آسیب پذیری در RSA پیامدهای امنیتی فاجعه باری خواهد داشت، بنابراین حملات مختلفی برروی آن انجام شده است.
قدرت RSA، با اندازه کلید آن اندازه گیری می شود که همان تعداد بیت ها در n=pq است. از زمانی که هکر ها موفق شدن با حمله های Brute Force مدرن کلید های خصوصی را در چند ساعت استخراج کنند، دیگر RSA های 512 بیتی (155 رقمی) امن نیستند. بعد از آن در سال 2010 حمله ی مشابهی توانست کلید خصوصی 768 بیتی (232 رقمی) را بدست آورد. در سال 2016 هم کلیدهای 1024 بیتی (309 رقمی) به عنوان کلیدهای غیر ایمن معرفی شدند. این روزها کلیدهای 4096 بیتی (1234 رقمی) به عنوان کلید های امن شناخته می شوند.
یک حمله رایج به RSA، که می تواند الگوریتم را به طور کلی دور می زند به این صورت است که یک کامپیوتر می تواند به سرعت بزرگترین مقسوم علیه دو عدد را با استفاده از الگوریتم اقلیدسی محاسبه کند، بنابراین مهاجم می تواند این الگوریتم را روی دو کلید عمومی اجرا کند. اگر بزرگترین مقسوم علیه مشترک آنها 1 نباشد، مهاجم یکی از اعداد اول را پیدا کرده است، حالا هر دو کلید را بر عدد اول پیدا شده تقسیم میکند، در نتیجه دو کلید را همزمان میشکند. به عنوان مثال، فرض کنید دو کلید عمومی 239149 و 166381 را داریم. الگوریتم اقلیدسی، می تواند نشان دهد که این دو عدد دارای بزرگترین مقسوم علیه مشترک 379 هستند.
حمله های دیگری هم که روی این الگوریتم موفق هستند هم به همین صورت، از ضعف در تعیین اعداد p و q حاصل می شوند.
دسته دیگری از حملات بر روی سخت افزار متمرکز هستند. با دستکاری سطوح توان یک کامپیوتر و ایجاد خطاهای برق، محققان میشیگان توانستند یک کلید خصوصی 1024 بیتی را تنها با استفاده از سخت افزار استاندارد و رایج رمزگشایی کنند. به طور مشابه، با مطالعه صداهایی که یک کامپیوتر در حین کار تولید می کرد، محققان اسرائیلی توانستند یک کلید خصوصی 4096 بیتی را در کمتر از یک ساعت استخراج کنند.
منابع
https://brilliant.org/wiki/rsa-encryption
https://en.wikipedia.org/wiki/RSA_(cryptosystem)
