
در درس قبل با مفهوم نمونهبرداری و برآوردهای نقطهای آشنا شدید و دیدید که چگونه میتوان با انتخاب بخشی از دادهها، به تخمینی قابل اتکا از کل جامعه آماری رسید. حالا در این قسمت یک قدم جلوتر میروید و وارد دنیای کاربردیتر و عملیتر نمونهبرداری میشوید.
در این فصل از دوره آموزشی نمونه برداری در پایتون ، چهار روش مهم نمونهبرداری تصادفی در پایتون را بررسی میکنید
- نمونهبرداری ساده
- نمونهبرداری سیستماتیک
- نمونهبرداری طبقهای
- نمونهبرداری خوشهای
نمونهبرداری تصادفی ساده
نمونهبرداری تصادفی ساده مانند قرعهکشی یا لاتاری عمل میکند. در این روش، هر عضو جمعیت شانس برابر برای انتخاب شدن دارد.
به عنوان مثال، در مجموعه داده دانههای قهوه، جمعیت ما از انواع مختلف قهوه تشکیل شده است. برای انجام نمونهبرداری تصادفی ساده، کافی است دانههای قهوه را به صورت تصادفی انتخاب کنیم. که هرقهوه شانس یکسانی در برابر انتخاب شدن دارد. در برخی موارد ممکن است دو نمونه مشابه یا نزدیک به هم انتخاب شوند، مانند دوتا دانه قهوه که ویژگیهای مشابه دارند.

گاهی نیز ممکن است در برخی مناطق بزرگ از مجموعه داده هیچ نمونهای انتخاب نشود. این اتفاق طبیعی است و از ویژگیهای روش تصادفی ساده است.
نمونهبرداری سیستماتیک
روش بعدی، نمونهبرداری سیستماتیک است.
- در این روش، نمونهها از جمعیت در فواصل معین انتخاب میشوند.
- به عبارت دیگر، بعد از تعیین فاصله نمونهگیری (مثلاً هر ۵ عضو)، نمونهها به صورت منظم و سیستماتیک از جمعیت انتخاب میشوند.

فرض کنید یک مجموعه داده از دانههای قهوه داریم:
- اگر بخواهیم از روش سیستماتیک استفاده کنیم، میتوانیم دانهها را از بالا به پایین و از چپ به راست مرتب کنیم و هر پنجمین دانه را به عنوان نمونه انتخاب کنیم.
- با این روش، نمونهگیری منظم و با فواصل ثابت انجام میشود و نیاز به انتخاب کاملاً تصادفی هر عضو نیست.
روش نمونهبرداری سیستماتیک نسبت به نمونهبرداری تصادفی ساده کمی پیشرفتهتر است، و بخش دشوار آن مشخص کردن فاصله نمونهگیری است. برای درک عملی این روشها، وارد Jupyter Notebook میشویم و نحوه پیادهسازی هر دو روش را بررسی میکنیم.
نمونهبرداری تصادفی ساده با Pandas
در بخش قبل، نمونهبرداری تصادفی ساده با استفاده از کتابخانه Pandas انجام شد. حال میتوانیم یک بار دیگر این روش را امتحان کنیم:
- ابتدا یک Data Frame ایجاد میکنیم و مجموعه داده مورد نظر را در آن قرار میدهیم.
- با فراخوانی متد
()sample، تعداد نمونهها را مشخص میکنیم.
برای مثال، اگر بخواهیم ۵ نمونه انتخاب کنیم:
# In [3]:
coffee_ratings.sample(n=5)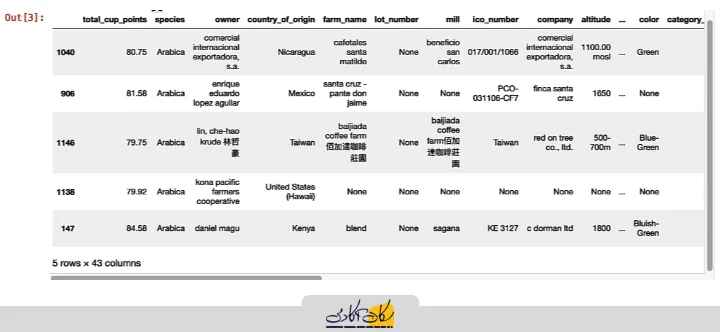
با این روش، نمونهبرداری تصادفی ساده انجام میشود و هر عضو جمعیت شانس برابر برای انتخاب شدن دارد.
یک نکته مهم هنگام استفاده از متد ()sample در Pandas این است که میتوانیم از آرگومان random_state استفاده کنیم. با تعیین یک عدد برای random_state، نتایج نمونهگیری قابل تکرار میشوند.
# In [5]:
coffee_ratings.sample(n=5, random_state=10019)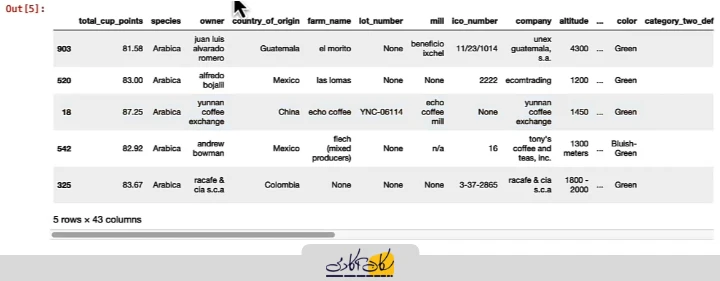
این ویژگی به ویژه زمانی مفید است که بخواهیم نتایج تحلیلها و مثالها همیشه یکسان باشند و سایر افراد بتوانند همان خروجی را مشاهده کنند. با اجرای کد بالا، همیشه همان ۵ نمونه انتخاب میشوند، حتی اگر چندین بار کد را اجرا کنیم. مقدار 19 در اینجا تنها یک مثال است و میتوان هر عدد دلخواهی به عنوان seed استفاده کرد
پیادهسازی نمونهبرداری سیستماتیک
فرض کنید میخواهیم نمونهای با اندازه ۵ از مجموعه داده Coffee Ratings انتخاب کنیم. برای پیدا کردن فاصله مناسب، اندازه کل جمعیت را بر اندازه نمونه تقسیم میکنیم:
# In [6]:
sample_size=5
# In [7]:
pop_size = len(coffee_ratings)
# In [8]:
pop_size
# Out[8]: 1338در اینجا، interval مشخص میکند که هر چند ردیف یک نمونه انتخاب شود. پس از تعیین فاصله، میتوانیم نمونهها را به صورت سیستماتیک از مجموعه داده انتخاب کنیم. برای تعیین فاصله نمونهگیری در روش سیستماتیک، از رابطه زیر استفاده میکنیم:
# In [6]:
sample_size=5
# In [7]:
pop_size = len(coffee_ratings)
# In [8]:
pop_size
# Out[8]: 1338
# In [10]:
interval = pop_size / sample_size
interval
# Out[10]: 267.6برای اینکه مجموعه داده را به فواصل 268 تایی تقسیم کنیم و نمونهگیری انجام دهیم، از ترکیب زیر استفاده میکنیم:
# In [11]:
interval = pop_size // sample_size + 1
interval
#Out[11]: 268
# In [12]:
coffee_ratings[::interval]علامت interval:: به Pandas میگوید هر ردیف interval ام را انتخاب کن. در این مثال، با فاصله 268، نمونهها به صورت منظم و سیستماتیک از مجموعه داده استخراج میشوند.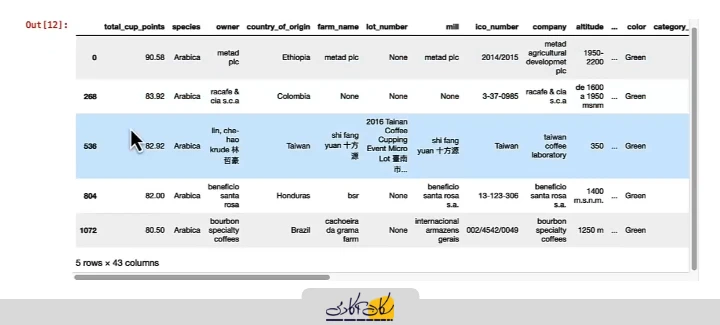
گاهی در نمونهبرداری سیستماتیک ممکن است ویژگیهایی از دادهها الگوی خاصی داشته باشند و نمونههای انتخاب شده همگی به یک بخش از این الگو بخورند. این موضوع میتواند باعث عدم نمایندگی کامل دادهها شود.
فرض کنید میخواهیم ستون Aftertaste در مجموعه داده Coffee Ratings را بررسی کنیم برای تحلیل الگو، میتوان از نمودار Scatter یا Scatter Plot استفاده کرد. قبل از رسم نمودار، بهتر است مجموعه داده نمونه یک ایندکس مرتب داشته باشد تا رسم نمودار دقیق انجام شود.
یک Data Frame موقت ایجاد میکنیم. با استفاده از متد ()reset_index، ایندکس Data Frame را ریست میکنیم:
# In [14]:
coffee_ratings_with_id = coffee_ratings.reset_index()
# In [15]:
coffee_ratings_with_idرسم نمودار با Matplotlib
اکنون میتوانیم Data Frame جدید که ایندکس آن ریست شده است را برای رسم نمودار Scatter استفاده کنیم و الگوی ستون Aftertaste را بررسی کنیم.
- محور X: ایندکس ردیفها (از Data Frame ریست شده)
- محور Y: مقدار ستون Aftertaste
این نمودار به ما کمک میکند الگوها یا روندهای موجود در ستون Aftertaste را به صورت بصری بررسی کنیم.
# In [16]:
coffee_ratings_with_id.plot(x='index', y='aftertaste', kind='scatter')
# Out[16]:
<AxesSubplot:xlabel='index', ylabel='aftertaste'>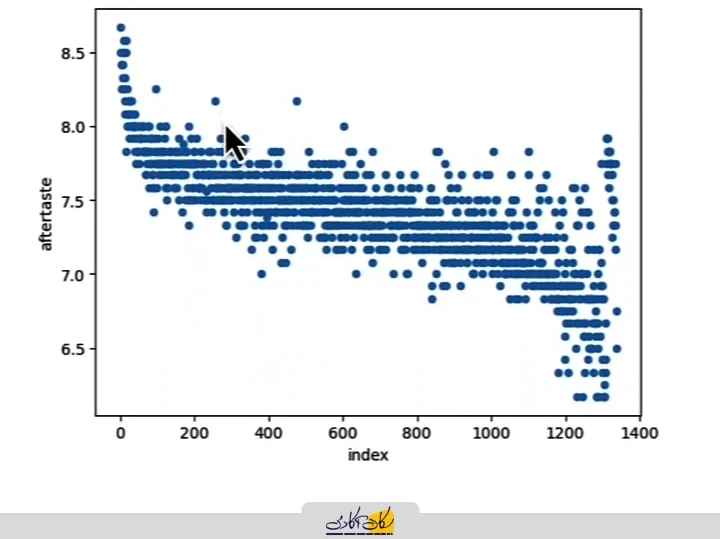
پس از اجرای نمودار Scatter برای ستون Aftertaste، مشاهده میکنیم که دادهها از یک الگوی مشخص پیروی میکنند:
- ردیفهای اولیه نسبت به ردیفهای بعدی امتیاز بالاتری دارند.
- این نشان میدهد که در دادهها یک ترتیب یا الگو موجود است.
- وقتی از نمونهبرداری سیستماتیک استفاده کنیم و فاصله ثابت (Interval) تعیین کنیم، این الگو میتواند باعث ایجاد بایاس در نمونه ما شود.
- بایاس به این معنا است که نمونه انتخاب شده نماینده واقعی جمعیت نیست و محاسبات آماری (مثل میانگین یا واریانس) دقیق نخواهد بود.
- بنابراین برای استفاده از نمونهبرداری سیستماتیک، مجموعه داده باید قبل از نمونهبرداری تصادفی شده باشد، به طوری که هیچ الگوی مشخصی در دادهها دیده نشود و دادهها شبیه نویز تصادفی باشند.
تصادفی کردن ترتیب دادهها در نمونه برداری سیستماتیک
برای جلوگیری از بایاس (Bias)، میتوان از متد ()sample در کتابخانه Pandas استفاده کرد تا ترتیب ردیفهای مجموعهداده پیش از انجام نمونهبرداری سیستماتیک، بهصورت تصادفی تغییر کند. متد ()sample دارای آرگومانی به نام frac است که مشخص میکند چه کسری از کل ردیفهای داده باید در نمونهی تصادفی بازگردانده شود. مقدار پیشفرض این پارامتر None است. برای مثال:
- اگر مقدار frac برابر با 0.5 قرار داده شود، ۵۰ درصد از ردیفهای مجموعهداده بهصورت تصادفی انتخاب میشوند.
- اگر مقدار frac برابر با 1 باشد، تمام ردیفهای مجموعهداده بازگردانده میشوند، با این تفاوت که ترتیب آنها بهطور کامل بهصورت تصادفی تغییر میکند.
# In [17]:
shuffled = coffee_ratings.sample(frac = 1)
# In [19]:
shuffledکه میبینیم ترتیب سطرها به این صورت هست
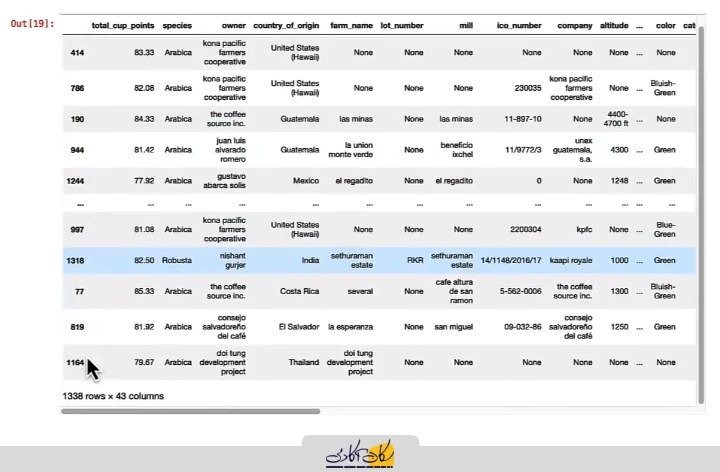
اکنون میتوان با فاصله مشخص (Interval) نمونهبرداری سیستماتیک را بدون نگرانی از بایاس انجام داد.
قبل از رسم نمودار، باید ایندکسها را دوباره ریست کنیم:
- این دستور ایندکسهای قدیمی را حذف میکند و یک ایندکس جدید از ۰ تا n-1 به Data Frame اضافه میکند.
- انجام این مرحله برای رسم نمودار و تحلیل دادهها ضروری است، زیرا محور X نمودار به ایندکسها وابسته است.
حالا میتوانیم دوباره ستون Aftertaste را بررسی کنیم:
- محور X: ایندکس جدید ردیفها
- محور Y: مقادیر ستون Aftertaste
# In [22]:
shuffled = shuffled.reset_index(drop=True).reset_index()
# In [23]:
shuffled.plot(x='index', y='aftertaste', kind='scatter')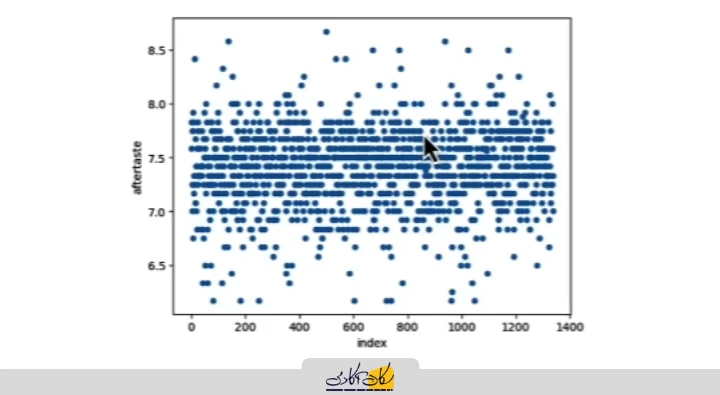
- با مشاهده نمودار، میبینیم که الگوی قبلی دیگر وجود ندارد.
- دادهها به صورت پراکنده و تصادفی (شبیه نویز) نمایش داده میشوند.
- این وضعیت شرط لازم برای نمونهبرداری سیستماتیک بدون بایاس را فراهم میکند و اکنون میتوانیم فاصله (Interval) را تعیین کنیم و نمونهها را به طور سیستماتیک انتخاب کنیم.
جمعبندی
در این قسمت با 2 روش مهم نمونهبرداری تصادفی شامل نمونهبرداری ساده، سیستماتیک، آشنا شدید و یاد گرفتید چگونه آنها را بهصورت عملی در پایتون پیادهسازی کنید. این روشها به شما کمک میکنند متناسب با ساختار دادهها، نمونهای دقیقتر انتخاب کرده و برآوردهای قابلاعتمادتری انجام دهید.
