آزمون t

در فصل دوم از آموزش آزمون فرض آماری با پایتون، ابتدا یاد می‌گیرید که چگونه با استفاده از آزمون t (آزمون تی) تفاوت میانگین‌ها را بین دو گروه بررسی کنید و در ادامه، با استفاده از آزمون آنووا (ANOVA) و آزمون‌های t زوجی یاد می‌گیرید که مقایسه را برای بیش از دو گروه انجام دهید.

در فصل قبل، Z-Score را محاسبه کردیم که در واقع یک آماره آزمون برای یک متغیر بود. اکنون در این قسمت، قصد داریم یک مسئله‌ی مرتبط اما متفاوت را بررسی کنیم؛ یعنی یک مسئله‌ی دو نمونه‌ای. در این مسئله، هدف ما بررسی آمار نمونه بین گروه‌های یک متغیر است. برای این کار به مجموعه داده‌ی استک اورفلو باز می‌گردیم.

متغیرهای دو نمونه‌ای

اگر به خاطر داشته باشید، در مجموعه‌داده‌ی Stack Overflow:

• یک متغیر عددی با نام converted_comp داریم که میانگین حقوق سالانه دیتا ساینتیست‌ها را نشان می‌دهد.
• یک متغیر دسته‌ای (Categorical) با نام age_first_code_cut داریم با دو سطح child و adult، که مشخص می‌کند کاربر برای اولین بار در چه سنی برنامه‌نویسی را آغاز کرده است.

سوالی که در این بخش قصد داریم به آن پاسخ دهیم، مربوط به تفاوت حقوق بین این دو گروه سنی است. سوال پژوهشی ما به این صورت مطرح می‌شود: آیا کاربرانی که برنامه‌نویسی را از دوران کودکی آغاز کرده‌اند، نسبت به افرادی که این کار را در بزرگسالی شروع کرده‌اند، حقوق سالانه‌ی بیشتری دریافت می‌کنند؟

پاسخ به این سوال، مثال خوبی برای آزمون t به عنوان یکی از روش‌های آزمون فرض آماری برای دو میانگین جامعه خواهد بود.

فرض‌های آماری در این مثال برای آزمون t

برای پاسخ به این سوال، فرض‌های آماری زیر را تعریف می‌کنیم:

• فرض صفر (Null Hypothesis): میانگین حقوق سالانه در هر دو گروه یکسان است.
• فرض مقابل یا جایگزین (Alternative Hypothesis): میانگین حقوق سالانه کاربرانی که از کودکی شروع به برنامه‌نویسی کرده‌اند، بیشتر از کاربرانی است که این کار را در بزرگسالی آغاز کرده‌اند.

در ادامه، این فرض‌ها را به‌صورت ریاضی و با استفاده از نمادهای آماری نیز نمایش خواهیم داد.

• μ Child: میانگین جمعیت کاربرانی است که از کودکی برنامه‌نویسی را آغاز کرده‌اند.
• μ Adult: میانگین جمعیت کاربرانی است که از بزرگسالی شروع به برنامه‌نویسی کرده‌اند.

در معادلات آماری، نماد μ (میو) نشان‌دهنده‌ی میانگین ناشناخته‌ی جامعه است. برای مشخص کردن این‌که هر میانگین متعلق به کدام گروه است، از زیرنویس (Subscript) استفاده می‌کنیم. به این ترتیب:

فرض صفر:

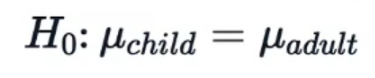
فرض مقابل:

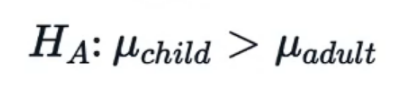
فرض‌های آماری را می‌توان به شکل معادل دیگری نیز بیان کرد. به‌جای مقایسه مستقیم دو میانگین، می‌توان تفاوت میانگین‌های جمعیت را با صفر مقایسه کرد. به عنوان مثال:

در ادامه، تحلیل خود را بر اساس همین فرم از فرض‌ها پیش می‌بریم. اکنون وارد محیط جوپیتر نوت‌بوک می‌شویم و دوباره نگاهی به مجموعه‌داده‌ی Stack Overflow می‌اندازیم.
همان‌طور که اشاره شد، در این تحلیل:

• ستون converted_comp را به‌عنوان متغیر عددی (حقوق سالانه) در نظر می‌گیریم،
• و ستون age_first_code_cut را به‌عنوان متغیر دسته‌ای که نشان می‌دهد کاربر از کودکی یا بزرگسالی برنامه‌نویسی را آغاز کرده است.

هدف ما مقایسه‌ی میانگین حقوق سالانه بین این دو گروه است.

محاسبه آمار

برای شروع، آمار خلاصه نمونه را برای هر یک از این گروه‌ها محاسبه می‌کنیم. برای این کار:

• مجموعه‌داده Stack Overflow را در نظر می‌گیریم،
• با استفاده از تابع groupby داده‌ها را بر اساس متغیر دسته‌ای age_first_code_cut گروه‌بندی می‌کنیم،
• و سپس تابع میانگین را روی متغیر عددی converted_comp اعمال می‌کنیم.

به این ترتیب، میانگین حقوق سالانه برای هر یک از دو گروه در سطح نمونه محاسبه می‌شود و می‌توانیم یک مقایسه‌ی اولیه بین آن‌ها انجام دهیم. برای محاسبه‌ی میانگین می‌توان از کتابخانه‌های NumPy یا Pandas استفاده کرد. در اینجا، از Pandas استفاده می‌کنیم و تابع میانگین را روی سری مربوطه اعمال می‌کنیم. با اجرای این محاسبات، نتایج زیر به دست می‌آید:

• میانگین حقوق سالانه برای کاربرانی که از کودکی برنامه‌نویسی را آغاز کرده‌اند، حدود ۱۳۲ هزار دلار است.
• میانگین حقوق سالانه برای کاربرانی که از بزرگسالی شروع کرده‌اند، حدود ۱۱۱ هزار دلار است.

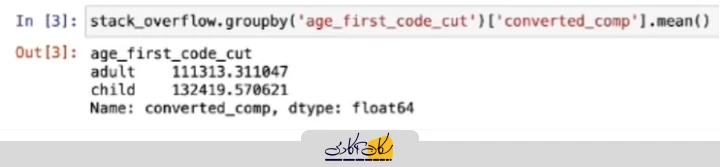
سوالی که مطرح می‌شود: آیا این تفاوت و افزایش مشاهده‌شده از نظر آماری معنادار است، یا می‌توان آن را با تنوع نمونه‌گیری توضیح داد؟ توجه داشته باشید که اگرچه میانگین واقعی جامعه را نمی‌دانیم، اما می‌توانیم آن را با استفاده از میانگین نمونه تخمین بزنیم. پیش از بررسی فرمول آزمون t، ابتدا متغیرهایی را که در آن استفاده می‌شوند مرور می‌کنیم:

استانداردسازی آماره آزمون t

برای استاندارد کردن آماره آزمون، همان منطق فصل قبل را به کار می‌گیریم. در فصل اول دیدیم که:

• میانگین مقدار آماره نمونه را در نظر می‌گرفتیم،
• آن را از پارامتر جمعیتی مورد نظر کم می‌کردیم،
• و نتیجه را بر خطای استاندارد تقسیم می‌کردیم.

اکنون، برای مسئله‌ی حاضر که یک مسئله‌ی دو نمونه‌ای است (به‌جای یک نمونه)، از تفاوت میانگین‌های نمونه استفاده می‌کنیم و یک معادله‌ی مشابه را به کار می‌بریم. در ادامه، این فرمول را به‌صورت دقیق بررسی کرده و از آن برای انجام آزمون t دو نمونه‌ای استفاده خواهیم کرد.

در آزمون دو نمونه‌ای، به جای استفاده از Z-Score  از T-Statistic استفاده می‌کنیم. مراحل محاسبه مشابه فصل قبل است، با این تفاوت که:

1. ابتدا تفاوت میانگین‌های نمونه را در نظر می‌گیریم.
2. سپس این مقدار را از تفاوت میانگین‌های جمعیت کم می‌کنیم.
3. حاصل را بر خطای استاندارد تفاوت میانگین‌ها تقسیم می‌کنیم.

محاسبه خطای استاندارد

برای محاسبه‌ی خطای استاندارد (Standard Error) که در مخرج فرمول T قرار می‌گیرد، چند روش وجود دارد:

1. بوت‌استرپینگ (Bootstrap): همانند فصل قبل، با نمونه‌برداری مجدد می‌توانیم توزیع میانگین‌ها را تولید کرده و خطای استاندارد را تخمین بزنیم.
2. روش تقریبی ساده‌تر:

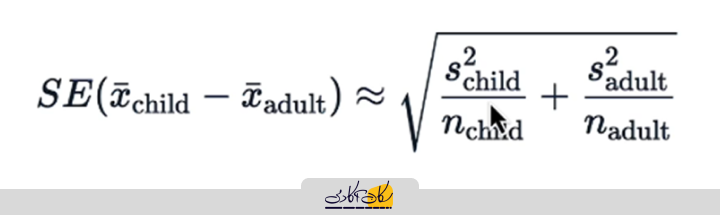
• ابتدا انحراف معیار متغیر عددی را برای هر گروه محاسبه می‌کنیم.
• سپس تعداد مشاهدات هر گروه را در نظر می‌گیریم.
• با استفاده از این مقادیر، خطای استاندارد تقریبی تفاوت میانگین‌ها را محاسبه می‌کنیم.

با فرض صحت فرض صفر (Null Hypothesis)، یعنی فرض اینکه میانگین‌های جمعیت برابر هستند میتونیم معادله را ساده سازی کنیم:

• تفاوت میانگین‌های جمعیت برابر صفر است.
• بنابراین این مقدار را از صورت کسر حذف می‌کنیم.

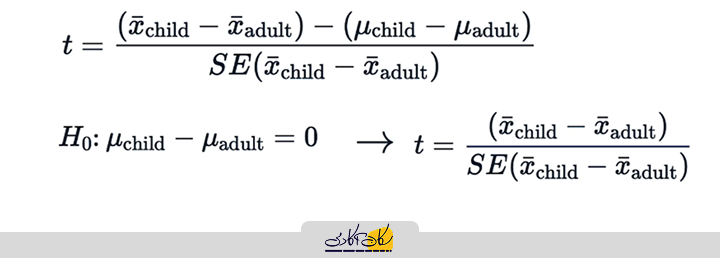
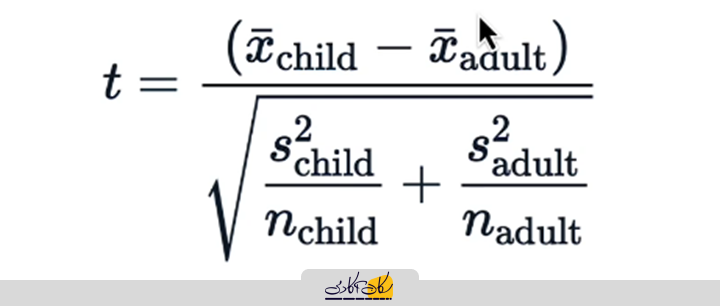
با جایگذاری خطای استاندارد تقریبی، فرمول T ساده می‌شود و تنها نیاز به انجام محاسبات روی مجموعه‌داده نمونه داریم.

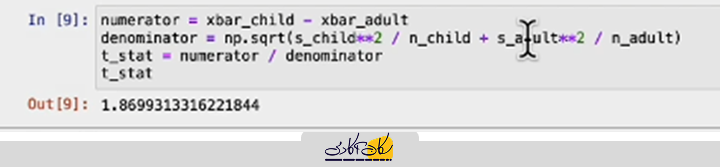
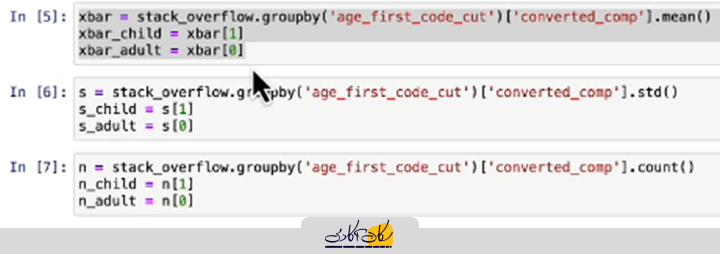
برای محاسبه‌ی آماره آزمون تی دو نمونه‌ای در محیط Jupyter Notebook، ابتدا باید موارد زیر را برای هر گروه محاسبه کنیم: ابتدا میانگین‌ها را که قبلاً محاسبه شده‌اند، در متغیر x_bar ذخیره می‌کنیم.

• سپس هر گروه را جدا می‌کنیم
• همین کار را برای انحراف معیار و تعداد مشاهدات انجام می‌دهیم

صورت کسر برابر است با تفاوت میانگین‌ها مخرج کسر برابر با خطای استاندارد تفاوت میانگین‌ها است و با استفاده از فرمول تقریبی محاسبه می‌شود:

• با اجرای این محاسبات، مقدار تقریبی T ≈ 1.87 به دست می‌آید.

تفسیر اولیه

• این مقدار شبیه یک Z-Score است و نشان می‌دهد که میانگین گروه‌ها چقدر از یکدیگر فاصله دارند.
• با این حال، برای نتیجه‌گیری قطعی، نیاز به بررسی سطح معنی‌داری و مقایسه با توزیع T داریم که در قسمت‌های بعدی این آموزش توضیح داده می‌شود.

بنابراین وارد قسمت بعدی شوید و با نمونه مثال و تمرین‌های عملی بیشتر، آموخته‌های خود در مورد محاسبات و مفاهیم آزمون t را تثبیت کنید.