تو این آموزش قراره که یکم بیشتر با پایتون کار کنیم
لئوناردو فیبوناچی از ریاضیدانان مشهور قرن سیزدهم میلادی به رابطهی جالبی میان اعداد دست یافت که دنبالهی این اعداد را سری فیبوناچی نام گذاشت. در این مقاله ، برنامه فیبوناچی با پایتون به معرفی اعداد و دنبالهی فیبوناچی میپردازیم و با روشهای مختلف حل آن با زبان پایتون آشنا میشویم .
سری فیبوناچی دقیقا چیه ؟ 🤔
0, 1, 1, 2, 3, 5, 8, 13, 21 ,34 ,55 ....دنبالهی فیبوناچی یا سری فیبوناجی دنبالهای از اعداد است . در این دنباله عدد بعدی با جمع دو عدد ماقبل خود به دست میآید ، پس داریم :
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
.........بقیه اعدد نیز به همین ترتیب محاسبه میشوند .
تولید مارپیچ (Spiral)
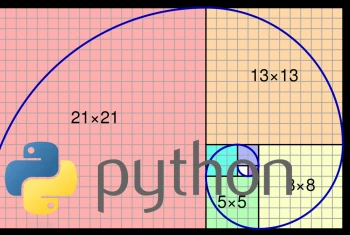
اگر مربعهایی با این عرضها درست کنیم ، یک مارپیچ خوشگل بدست میاریم :
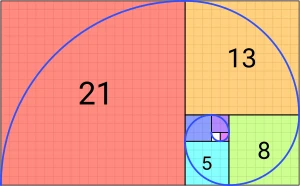
میبینید که مربعها چگونه در کنار هم قرار گرفتند ، با نظم خاصی که در دنبالهی فیبوناچی ظاهر شدهاند.
الگوی فیبوناچی در طبیعت یافت میشود ، برای مثال داریم :
گیاهان میتوانند سلولهای جدید را در الگوی مارپیچی تولید کنند ، مثل الگوی دانهها در شکل زیر:

یا الگوی فیبوناچی در صدف های دریایی :

دنباله فیبوناچی در طبیعت خیلی زیاد یافت میشود و کاربر فراوانی در ریاضیات و... دارد
با کمک ریاضیات میتوان دنباله فیبوناچی را به شکل زیر بنویسیم
Fn = Fn-1 + Fn-2
یعنی مقدار هر عنصر جدید را میتوان به کمک مجموع دو عنصر قبلی و طبق یک رابطهی بازگشتی نوشت .
در کد زیر دنبالهی فیبوناچی را به کمک توابع بازگشتی مینویسیم. ابتدا شرایط بازگشت را با عبارت شرطی if و با بررسی مقادیر اولیه تعریف کرده و سپس طبق روال توابع بازگشتی، مقدار تابع بازگشتی را بر اساس مقادیر قبلی به شکل جملهی nام سری فیبوناچی، تعریف میکنیم:
def fibonacci(n):
if n<0:
print("Invalid input")
elif n==0:
return 0
elif n==1:
return 1
else:
return fibonacci(n-1)+fibonacci(n-2)
print(fibonacci(5))منظور از مقدار دهی اولیه یعنی برای عدد 0 و ۱ خود آنها را برگردانیم
خروجی را به ازای مقدار ۷ بررسی میکنیم. یعنی مقدار جملهی هفتم دنباله را محاسبه میکنیم :
که خروجی برای ما ۱۳ خواهد بود
پیچیدگی زمانی این کد به صورت (T(n) = T(n-1) + T(n-2 است . کدنویسی به روش بازگشتی موجب بروز کارهای تکراری و در نهایت باعث افزایش زمان اجرای برنامه میشود .
برای جلوگیری از تکرار محاسباتی، از روش برنامهریزی دینامیک یا پویا استفاده میکنیم . به طوری که نتیجهی عملیاتی محاسباتی را در هر مرحله در داخل یک لیست ذخیره کنیم و در صورت نیاز مجدد، آن را از لیست به دست بیاوریم . در این صورت زمان اجرای برنامه از مرتبهی خطی خواهد بود. در کد زیر محاسبهی اعداد فیبوناچی به روش برنامهنویسی پویا رو داریم :
def fibonacci(n):
fibArray = [0, 1]
while len(fibArray) < n + 1:
fibArray.append(0)
if n <= 1:
return n
else:
if fibArray[n - 1] == 0:
fibArray[n - 1] = fibonacci(n - 1)
if fibArray[n - 2] == 0:
fibArray[n - 2] = fibonacci(n - 2)
fibArray[n] = fibArray[n - 2] + fibArray[n - 1]
return fibArray[n]
print(fibonacci(9))این مفهوم ساده و پایهای کاربرد گستردهای در طبیعت و... دارد
ما میتوانیم الگوریتم فیبوناچی رو با روش های دیگری حل و بهینه تر کنیم ، اما در این آموزش ما از توابع بازگشتی استفاده کردیم که ساده ترین و مرسوم ترین روش در پیاده سازی این الگوریتم هست
موفق پیروز باشید ❤️