نظریه بازی (Game theory) در یک تعریف کلی زیرمجموعهای از علم ریاضیات است که میتواند با استفاده از تحلیل کردن یک سری از سناریوها و طراحیها، رفتارها و نتایج تصمیمگیری افراد را پیشبینی کند.
در یک تعریف کلی نظریه بازی، علم استراتژی یا به عبارتی تصمیمگیری درست در واکنش به رقبا در یک فضای استراتژیک است.
با استفاده از این نظریه، سناریوهای دنیای واقعی برای شرایطی مثل رقابت، قیمتگذاری، انتشار محصول و... را میتوان مطرح کرد و نتایج آنها را پیشبینی کرد.
بهوسیله نظریه بازی، شرایط پیچیده تعامل انسانها، سازمانها، کشورها، کسبوکارها و اقتصاد افراد درگیر بازی ساده میشود و با تشخیص گزینههای پیش رو و معادلات بازی، احتمال وقوع حرکت بعدی رقیب تا حد امکان قابل پیشبینی میشود.
نظریه بازی چگونه شکل گرفت؟
سال 1921 امیل بورل(Emile Borel) شروع به بررسی تعدادی از بازیهای قمارخانهها کرد و چندین مقاله در این خصوص نوشت.در این مقالهها به قابل پیشبینی بودن نتایج این نوع بازیها از روشهای منطقی، تأکید کرده بود. بعد از بورل، جان فون نویمان (John von Neumann)ریاضیدان مجارستانی در سال 1928 نظریه بازی را توسعه داد و دلیل آن علاقهمندی به بازی ورق (Card game) بود. او متوجه شده بود که نتیجه این بازی صرفاً با تئوری احتمالات مشخص نمیشود بلکه افراد درگیر بازی بهوسیله بلوف زدن مقداری از اطلاعات بازی را از رقیب خود پنهان میکنند.
در مثالی از کاربرد تئوری نظریه بازی، نفون نویمان توانست بهوسیله استراتژی موجود در بازی شطرنج، کنشهای میان ایالاتمتحده و اتحاد جماهیر شوروی را در جنگ سرد با در نظر گرفتن آنها بهعنوان دو بازیکن در یک «بازی با مجموع صفر»، مدلسازی کند.
در سال 1994 نیز جان فوربز نش (John Forbes Nash) به همراه دو تن دیگر به دلیل مطالعات خلاقانه در نظریه بازی برنده جایزه نوبل اقتصاد شدند.
نظریه بازی چگونه کار میکند؟
محوریت نظریه بازی این است که نتیجه بازی یک بازیکن مشروط به استراتژی اجرا شده توسط بازیکن دیگر است.
نظریه بازی تلاش میکند تا رفتارهای حاکم بر یک موقعیت استراتژیک را مدلسازی کند. این موقعیت، زمانی به وجود میآید که موفقیت یک فرد وابسته به راهبردهایی باشد که دیگران انتخاب میکنند. هدف این دانش، پیدا کردن بهترین استراتژی برای بازیکنان است. نظریه بازی گستره وسیعی از کاربردها ازجمله در روانشناسی، زیستشناسی تکامل، جنگ، سیاست، اقتصاد و کسب کار دارد و به تحلیل رفتار منطقی متقابل انسانها، حیوانات و رایانهها میپردازد.
کاربردهای نظریه بازی
هر جا که منابع افراد محدود باشد و گزینههای مختلفی برای تصمیمگیری پیش رو باشد و بهواسطه انتخابهای متفاوت خروجی و دستاوردهای متفاوتی وجود داشته باشد و یا امکان همکاری و رقابت بین بازیگران وجود داشته باشد،میشود از نظریه بازی برای تحلیل بهتر شرایط استفاده کرد.
استفاده از نظریه بازی در تعاملات سیاسی، اقتصادی و اجتماعی
نظریه بازی با پرداختن به مشکلات اساسی در مدلهای اقتصادی، انقلابی در اقتصاد ایجاد کرد، بهعنوانمثال، اقتصاد نئوکلاسیک برای درک انتظار کارآفرینی تلاش میکرد اما نمی توانست از پس رقابت بر بیاید.نظریه بازی توجه را از تعادل حالت پایدار به روند بازار معطوف کرد.
نمونه های کاربردی نظریه بازی:
- رفتار شرکتها در مورد قیمتگذاری محصول در شرایط انحصار
- معاملات بورس و رمز ارزها و واکنش و تصمیم سرمایهگذاران در مقابل تحولات بازار
- تصمیم کشورهای حوزه اوپک برای میزان استخراج نفت و فروش نفت و میزان تعهد و عدم تعهد آنها به توافقات صورت گرفته
تعریف فضای بازی
در این بخش به معرفی عناصر بازی برای بهتر مشخص شدن فضای بازی میپردازیم:
1. بازیکنان (players): طرفهای بازی هستند که هرکدام حداقل دو استراتژی را در اختیار دارند.
2. راهبرد (Strategy): رویکردی است که برای تعیین اقدامات و واکنشها بر اساس شرایط خود و حرکات حریف از آن استفاده میشود.
3. کنشها (Actions): زنجیرهای از اقدامات است که بازیکن در شرایط مختلف بازی انجام میدهد.
4. بازده (Payoffs): سود مورد انتظار یا مطلوب که بازیکن انتظار دارد در یک بازی حاصل کند.
5. اطلاعات (Information): اینکه در هرلحظه از بازی هر بازیکن چه اطلاعاتی را میتواند از حرکتهای طرف مقابلش بداند.
6. نتیجه بازی (Outcome): وقتی بازی به انتها میرسد چه نتایجی به بار میآید.
انواع بازی
نظریه بازی میتواند روند و نتیجهٔ هر نوع بازی از بازی دوز گرفته تا بازی در بازار رمز ارزها را توصیف و پیشبینی کند.
تعدادی از ویژگیهایی که بازیهای مختلف بر اساس آنها طبقهبندی میشوند، در زیر آمده است. اگر کمی دقت کنید ازاینپس میتوانید خودتان بازیهای مختلف و یا حتی پدیدهها و رویدادهای مختلفی را که پیرامون خود با آنها مواجه میشوید را به همین ترتیب تقسیمبندی کنید.
1. بازی با مجموع صفر (Zero-sum Game): در این بازی سود یک بازیگر معادل زیان بازیگر دیگر است.
2. بازی با مجموع غیر صفر (Non zero sum Game): در این بازی تصمیمات یک بازیگر ممکن است به نفع همه بازیگران باشد.
3. بازی تعاونی (Cooperative Game): در این نوع بازی امکان سازش و تبانی با دیگران وجود دارد.
4. بازی غیرتعاونی (Non-Cooperative Game): در این نوع بازی امکان سازش و تبانی بین شرکتکنندگان وجود ندارد.
همگی با بازی ضربدر و دایره (Tic Tac To game) آشنایی دارید. احتمالاً هنگام بازی کردن یک استراتژی را برای بردن انتخاب کردهاید و منتظر هستید تا حریف شما اشتباهی انجام داده تا از آن به بهترین نحو استفاده و بازی را به نفع خود تمام کنید.
این بازی ساده، الزامات مربوط به یک بازی در نظریه بازیها و قواعد تصمیم را دارد. قواعد بازی، نحوه برنده یا بازنده شدن، امکان تکرار بازی و ثبت امتیازات از ویژگیهایی یک بازی است که در اینجا نیز به چشم میخورد. در این بازی مجموعه قوانینی وجود دارد که بازیکنان مجبور به رعایت آنها هستند. برای مثال میتوان قانونهای این بازی را بهصورت زیر مشخص کرد.
• در این بازی در هر خانه بیش از یک علامت نمیتوان قرار داد.
• بازی بهصورت نوبتی انجام میشود. به این معنی که در هر بار فقط یک بازیکن امکان ترسیم علامت در داخل جدول را دارد.
• هر بازیکن باید از علامت خاص خود استفاده کند. برای مثال بازیکنی که با علامت X شروع کرده است تا انتهای بازی باید این علامت را در خانههای جدول قرار دهد.
• هرگاه سه خانهای از جدول که روی یک خط راست قرار دارند، با یک علامت پر شده باشد بازی خاتمه یافته و صاحب علامت برنده اعلام میشود.
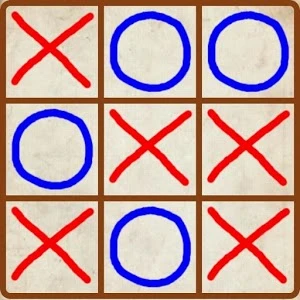
استراتژی بازی X O نحوه پیروزی را مشخص میکند. تا حد ممکن نباید به حریفتان اجازه دهید که سه علامت در یک خط راست ایجاد کند. از طرفی باید این کار را باقدرت تمام برای خودتان انجام دهید.
بهاینترتیب هنگام بازی از یک استراتژی خاص پیروی میکنید. استراتژی، یک برنامه کلی و کامل است که مشخص میکند چه حرکتی در چه موقعیت یا زمانی ممکن است رخ داده تا نتیجه بازی را به نفع شما برگرداند. در بازیهای ساده و با اطلاعات کامل، با رعایت این استراتژی بهطور قطعی بازی را خواهید برد. درصورتیکه در یک بازی، تمامی قوانین، گزینههای ممکن و سابقه و مراحل، قابل مشاهده باشد، آن را «بازی با اطلاعات کامل (Perfect Information Game) مینامند. بازیهایی مانند شطرنج و بازی X O از این گروه بازیها در نظریه بازیها محسوب میشوند.
نظریه بازی در زندگی واقعی به عوامل متعددی بستگی دارد.حتی اگر از فرمولهای مختلف برای خروجی و نتیجه بازی استفاده شود، به یک حس مشترک و درک آن نیاز است. نظریه بازی در بخشهای مختلف درحالتوسعه است و سعی میکنیم در چندین قسمت به ابعاد مختلف این نظریه بپردازیم.
