تحلیل الگوریتمی چیست و چگونه انجام می‌شود؟

در مقاله قبل گفتیم که الگوریتم یک فرآیند گام به گام برای حل یک مسئله محاسباتی است. به بیان دقیق‌تر، الگوریتم شامل فهرستی از دستورالعمل‌‌هایی است که برای حل یک مسئله باید رعایت شود. بر همین اساس، مهم است در هنگام نوشتن الگوریتم، دستوراتی که باید اجرا شوند به ترتیب نوشته شوند تا خروجی مدنظر دریافت شود. هنگامی که قصد نوشتن الگوریتمی را داریم باید به دو نکته مهم دقت کنیم:

1. الگوریتم چه مدت زمانی طول می‌کشد تا یک وظیفه محاسباتی را انجام دهد
2. به چه میزان از منابع مهم سیستمی مثل پردازنده مرکزی یا حافظه اصلی استفاده می‌کند.

برای این منظور باید با مبحثی که تحلیل الگوریتمی نام دارد آشنا باشیم.

الگوریتم چیست؟

قبل از آن‌که، به سراغ مبحث تحلیل الگوریتمی برویم، اجازه دهید تعریف کوتاهی در ارتباط با الگوریتم ارائه کنیم. الگوریتم مجموعه‌ای متناهی از دستورالعمل‌هایی است که ترتیب خاصی دارند و قرار است، مسئله‌ای را حل کنند. به عبارت دقیق‌تر، الگوریتم، روشی مرحله به مرحله برای حل مسئله است. در دنیای برنامه‌نویسی، الگوریتم مجموعه‌ای از دستورالعمل‌ها است که برای حل یک مسئله خاص استفاده می‌شود. الگوریتم مجموعه‌ای از ورودی‌ها را دریافت می‌کند و خروجی مدنظر برنامه‌نویس را ارائه می‌کند. به‌طور مثال، الگوریتم جمع دو عدد به شرح زیر است:

1. دو عدد به عنوان ورودی دریافت می‌شود. 
2. اعداد با استفاده از عملگر + با یکدیگر جمع می‌شوند. 
3. نتیجه نمایش داده می‌شود.

نکته مهمی که باید به عنوان یک برنامه‌نویس به آن دقت کنید این است که کامپیوترها، تجهیزات الکترونیکی غیر هوشمندی هستند که تنها بر مبنای دستوراتی که در قالب برنامه در اختیار آن‌ها قرار می‌گیرد، قادر به انجام کار مشخصی هستند. 

الگوریتم بنویسیم یا فلوچارت؟

در زمان‌های قدیم، دانشگاه‌ها و موسسات آموزشی، مبحث برنامه‌نویسی را با فلوچارت‌سازی و الگوریتم‌نویسی به دانشجویان آموزش می‌دادند. متاسفانه، در سال‌های اخیر این موضوع کم رنگ شده و برخی برنامه‌نویسان اطلاع چندانی در ارتباط با مبحث فلوچارت‌سازی ندارند و تنها به فکر تکمیل سریع یک پروژه برنامه‌نویسی بر مبنای ماژول‌ها و افزونه‌های از پیش ساخته شده‌اند. اکنون، این پرسشی مطرح است هنگامی که پروژه‌ای را دریافت می‌کنیم باید به فکر فلوچارت‌سازی برای آن باشیم؟ پاسخ مثبت است. فلوچارت‌ها کمک می‌کنند بدون مشکل الگوریتم‌ها را بنویسیم و الگوریتم‌ها کمک می‌کنند به شکل دقیقی برنامه‌های کاربردی را توسعه دهیم. بر مبنای این تعریف، باید بگوییم که فلوچارت‌ها سلاح پنهان برنامه‌نویسان هستند. فلوچارت‌ها، ضمن این‌که روند کلی طراح را در قالب نمودارها و اشکال نشان می‌دهند، امکان بروز خطا در کدنویسی را به حداقل می‌رسانند، اما فلوچارت چیست؟ فلوچارت مجموعه‌ای از اشکال قراردادی است که دستورالعمل‌ها و ترتیب اجرای دستوراتی که قرار است در الگوریتم درج شوند را نشان می‌دهند. اجازه دهید، برای روشن شدن بحث به مثال ساده‌ای اشاره کنیم. فرض کنید، در نظر داریم، فلوچارت و الگوریتمی بنویسیم که 5 عدد را از ورودی بخواند، مجموع و میانگین آن‌ها را محاسبه کند و نمایش دهد. فلوچارت این تمرین به شرح زیر است:

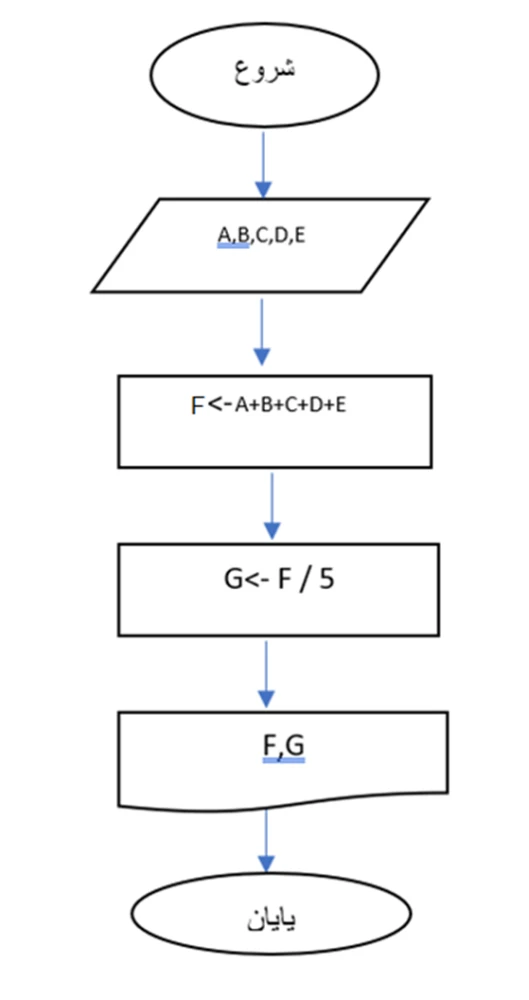
اکنون بر مبنای فلوچارت فوق، الگوریتم آن‌را به شرح زیر می‌نویسیم:

1. شروع.

2. پنج عدد را بخوان و در متغیرهای A، B، C، D و E قرار بدهد.

2. حاصل عبارت  A + B + C + D + Eرا در متغیر F قرار بدهد. 

3. حاصل تقسیم F بر 5 را در متغیر G قرار بده.

4. مقادیر F و G را نشان بده.

6. پایان

همان‌گونه که مشاهده می‌کنید، فلوچارت‌نویسی و الگوریتم‌نویسی به شکل قابل توجهی روند ساخت برنامه‌های کاربردی را ساده‌تر می‌کند. 

تحلیل الگوریتمی چیست؟

تحلیل الگوریتمی بخش مهمی از نظریه پیچیدگی محاسباتی است که تخمین نظری در ارتباط با منابع مورد نیاز یک الگوریتم برای حل یک مسئله محاسباتی خاص ارائه می‌دهد. 

نوشتن یک الگوریتم

قبل از این‌که بتوانیم یک الگوریتم را تجزیه و تحلیل کنیم، ابتدا باید آن‌را بنویسیم. بنابراین اجازه دهید الگوریتمی به شرح زیر بنویسیم: 

Algorithm Swap(a,b):
    temp = a
    a = b
    b = temp
return

شبه‌کد بالا، یک الگوریتم ساده مبتنی بر دستور زبان پایتون است. همان‌گونه که اطلاع دارید، الگوریتم‌ها مستقل از گرامر یک زبان هستند. در قطعه کد بالا از دستورات پایتون به این دلیل استفاده کردیم تا نقطه شروع الگوریتم، دستورات درون الگوریتم و مکانی که الگوریتم به پایان می‌رسد را نشان دهیم. 

تجزیه و تحلیل یک الگوریتم

اکنون که اطلاعات کلی در ارتباط با نحوه‌ی نوشتن یک الگوریتم به‌دست آوردیم، قصد داریم به سراغ تحلیل یک الگوریتم برویم. هنگامی که صحبت از تحلیل الگوریتم‌ها به میان می‌آید، چهار مسئله زیر اهمیت ویژه‌ای پیدا می‌کنند:

1. زمان
2. حافظه
3. مصرف داده (الگوریتم چقدر داده مصرف می‌کند)
4. مصرف انرژی

ما در این مقاله تنها روی مبحث تحلیل زمانی و مکانی تمرکز خواهیم کرد که هر دو با نماد Big O نشان داده می‌شوند.

زمان صرف شده توسط یک الگوریتم

هنگامی که الگوریتمی نوشته می‌شود، مهم‌ترین نکته‌ای که باید به آن دقت کنید این است که چه مدت زمانی طول می‌کشد تا یک الگوریتم وظیفه خاصی را انجام دهد. فرض کنید الگوریتمی نیاز داریم که کوتاه‌ترین مسیر بین A.B.C.D را پیدا کند و پاسخ را به کاربر برگرداند. ما ابتدا الگوریتم را می‌نویسیم و بعد آن‌را بررسی می‌کنیم تا ببینیم مدت زمان صرف شده برای انجام این کار چقدر است. به طور معمول، برنامه‌نویسان و تیم‌های نرم‌افزاری همواره به دنبال نوشتن الگوریتم‌هایی هستند که یک کار مشخص را در کوتاه‌ترین زمان ممکن انجام دهد. 

اجازه دهید کار را به صورت زیر آغاز کنیم: 

یک دستور مستقیم ساده در یک الگوریتم به یک واحد زمانی نیاز دارد.

مثال:

Temp=a

دستور فوق یک واحد زمانی است. 

A=b

دستور فوق نمونه دیگری از یک واحد زمانی است.

دستورات فوق کاملا مستقیم هستند، زیرا هیچ الگوریتم یا متدی را فراخوانی نمی‌کنند. به بیان دیگر، دستورات تو در تو (Nested) نیستند.

اکنون اجازه دهید، تحلیل زمانی تابعی که پیش‌تر نوشته بودیم را انجام دهیم.

Algorithm swap(a,b):
temp = a
a = b
b = temp
return

اولین کاری که باید انجام دهیم، شمارش تعداد دستورات الگوریتم فوق است. در الگوریتم فوق دستورات زیر را داریم:

Temp=a

A=b

B=temp

هر کدام از دستورات فوق یک واحد زمانی را به خود اختصاص می‌دهند. 

temp = a (1)
a = b (1)
b = temp (1)

بنابراین تابع f(n) ما 3 است که یک مقدار ثابت است. هر عدد صحیح به عنوان یک مقدار ثابت در نظر گرفته می‌شود.

با مشاهده الگو متوجه می‌شویم که تمام دستورات انتساب یک واحد زمانی را به خود اختصاص می‌دهند. از این‌رو، می‌توانیم مقادیر ثابت را با O(1) نشان دهیم که بیان‌گر این موضوع است که تمام اعداد صحیح O(1) هستند.

اکنون، زمان آن رسیده تا پیچیدگی فضایی این الگوریتم را تحلیل کنیم:

برای تحلیل پیچیدگی فضا به سراغ متغیرهای b ،a و temp می‌رویم. در مجموع ما از سه متغیر استفاده کرده‌ایم. در نتیجه پیچیدگی فضایی ما O(3) است. ما می‌توانیم، پیچیدگی زمانی را به دو روش شمارش گام و نمادهای مجانبی محاسبه کنیم.

شمارش گام (Frequency Count)

شمارش گام تعداد دفعاتی که قرار است یک دستور اجرا شود را مشخص می‌کند. به بیان دقیق‌تر، چند مرتبه دستوری در یک الگوریتم اجرا می‌شود. این امکان وجود دارد تا برای محاسبه‌ی این مقدار بر مبنای چهار خط ‌مشی زیر کار کنیم:

برای نظرات و اعلان‌ها، تعداد گام‌ها را 0 در نظر می‌گیریم، زیرا نظرات اجرا نمی‌شوند و هنگام نوشتن الگوریتم به اعلان‌ها نیازی نیست.

برای دستورات بازگشتی و انتساب تعداد گام‌ها 1 در نظر گرفته می‌شود، دستور انتساب مقداری را به متغیری اختصاص می‌دهد. به همین ترتیب، دستور return، تنها یک مقدار را باز می‌گرداند.

به همین دلیل، بهتر است تنها نماهایی که مرتبه بالاتر دارند را در نظر بگیرید. به عنوان مثال، در عبارت 3n2+4n، ما فقط 3n2 را در نظر می‌گیریم، به دلیل این‌که مرتبه بالاتری دارد. همچنین، در نمونه فوق، ضرایب ثابت را نادیده می‌گیریم، به‌طوری‌که در 3n2 ضریب ثابت مقدار 3 است که از آن صرف نظر می‌کنیم. در این حالت تنها n² باقی می‌ماند. اکنون، پیچیدگی زمانی O(n²) را داریم. اجازه دهید، برای درک بهتر موضوع به چند مثال اشاره کنیم:

Algorithm Sum(A,n): 
s = 0
for i in range(A)
s = s + A[i]
return s 

الگوریتم بالا آرایه‌ای با اندازه‌ی مشخصی را نشان می‌دهد. فرض کنید، آرایه 5 عنصر دارد که عناصر آن 6، 5، 10، 6 و 9 هستند. 

A آرایه ما و n تعداد عناصر آن است. الگوریتم بالا مجموع تمام عناصر آرایه را محاسبه می‌کند. اکنون، در نظر داریم زمان صرف شده توسط الگوریتم را پیدا کنیم، این کار را با یافتن روش شمارش گام و چهار قانونی که پیش‌تر اشاره کردیم، انجام می‌دهیم.

اولین کاری که باید انجام دهیم، شکستن الگوریتم است. 

در ابتدا متغیر i با 0 مقداردهی اولیه می‌شود، زیرا یک حلقه for داریم. می‌دانیم که الگوریتم ما به تعداد مشخصی تکرار می‌شود و این تعداد دفعات n است. اکنون، زمان محاسبه رسیده است. 

i = 0

i = 1

i = 2

i = 3

i = 4

i = 5

حلقه متوقف می‌شود و مقدار s را برمی‌گرداند، این زمانی است که حلقه درون الگوریتم تمام می‌شود. منطق انجام این‌کار به شرح زیر است: 

,0 < n و i = 0

,1 < n و i = 1

,2 < n و i = 2

,3 < n و i = 3

,4 < n و i = 4

,5 > n و i = 5

حلقه در i = 5 متوقف می‌شود، زیرا 5 بزرگ‌تر از n است.

شرط حلقه، 5 مرتبه ارزیابی می‌شود. چهار مرتبه شرط درست i < n و مرتبه پنجم نادرست، i > n ارزیابی می‌شود. حلقه ما برای n + 1 بار اجرا می‌شود.

جمع‌بندی

Algorithm Sum(A,n): 0
s = 0
for i in range(A): n+1
s = s + A n(1) 
return s 

در خط اول الگوریتم دستور Sum(A,n) را داریم. با توجه به این‌که تنها یک اعلان است، تعداد گام‌ها 0 در نظر گرفته می‌شود. 

در خط دوم الگوریتم s=0 را داریم که یک دستور انتسابی است و مقدار 1 را برای آن در نظر می‌گیریم.

در خط سوم الگوریتم، دستور for I in rage(A) به مفسر می‌گوید، قصد داریم حلقه‌ای برای شمارش مقادیر آرایه ایجاد کنیم. در این‌جا حلقه ما n + 1 بار تکرار خواهد شد. 

در خط چهارم الگوریتم، ;s = s + A[i] وجود دارد که یک دستور انتسابی است، زیرا ما عبارت s + A[i] را به متغیر s اختصاص می‌دهیم و به ‌دلیل این‌که دستور فوق در یک حلقه قرار دارد، n را به عنوان مقدار آن در نظر می‌گیریم. دقت کنید، درست است که دستور فوق انتسابی است و باید مقدار ثابتی برای آن در نظر بگیریم، اما به دلیل این‌که در حلقه قرار دارد و n مرتبه تکرار می‌شود، به جای یک مقدار ثابت، مقدار n را به آن اختصاص می‌دهیم. 

در خط 5 الگوریتم، دستور return s را داریم. از آن‌جایی که یک عبارت بازگشتی است، تعداد گام‌ها 1 است.

اکنون زمان محاسبه مقادیری است که به هر یک از دستورات اختصاص داده‌ایم. 

1+n+1+n+1 = 2n + 3
2n + 3

ما فقط نماهای مرتبه بالاتر را در نظر می‌گیریم، این حرف به این معنا است که تنها 2n باقی مانده است. همان‌گونه که اشاره کردیم از ضرایب ثابت صرف نظر می‌کنیم که باعث می‌شود تنها n باقی بماند که در نهایت O(n) را خواهیم داشت. 

اکنون وقت آن رسیده تا پیچیدگی فضایی الگوریتم را بررسی کنیم. برای این منظور به سراغ شمارش متغیرها در الگوریتم خود می‌رویم که s، A، n  و i هستند. 

(A آرایه ما است که n عنصر دارد، بنابراین پیچیدگی زمان آن n است) A = n 

 (s فقط یک عنصر را دریافت می‌کند) s = 1 

 (n فقط یک عنصر را دریافت می‌کند) n = 1 

 (i فقط یک عنصر را دریافت می‌کند) i = 1 

تنها کاری که باید انجام دهیم یک شمارش آماری ساده است. 

n+1+1+1+1 = n + 4

بازهم تنها نماهای مرتبه بالاتر برای ما مهم هستند، در نتیجه تنها n را داریم که پیچیدگی زمانی آن برابر با O(n) است.

برای روشن شدن بحث، اجازه دهید به ذکر مثال دیگری بپردازیم. به شبه‌کد زیر دقت کنید:

Algorithm Add(A,B,n):
for i in range(A):
for j in range(A):
C = A + B
return

در مثال بالا، دو حلقه تو در تو داریم که در اصطلاح تخصصی به آن‌ها outer loop و inner loop  می‌گوییم. اگر با دقت بیشتری به مثال فوق دقت کنید، متوجه می‌شوید، یک آرایه دو بعدی داریم که به صورت n*n نشان داده می‌شود. الگوریتم مجموع دو مقدار را محاسبه می‌کند. 

Algorithm ADD(A,B,n): 0
for i in range(A): n+1
for j in range(A): n(n+1)
c = A + B n(n)
return     1

در خط اول، دستور ADD(A,B,n) را داریم که از آن صرف‌نظر می‌کنیم، زیرا تنها یک تعریف است.

در خط دوم حلقه for خارجی وجود دارد که تعداد گام‌های آن n+1 است.

در خط سوم، حلقه for داخلی را داریم که تعداد گام‌های خود حلقه برابر با n+1 است، اما از آن‌جایی که درون حلقه دیگری اجرا می‌شود، برای حلقه دوم تعداد گام n نیز به آن افزوده می‌شود. به همین دلیل، تعداد گام‌ها برابر با n (n+1) است. دقت کنید، اگر حلقه تنها یک مرتبه اجرا شود، بازهم مرتبه زمانی n+1 را خواهیم داشت. 

در خط چهارم c = A + B را قرار دارد. دستور فوق در هر دو حلقه for اجرا می‌شود. به بیان دقیق‌تر، حلقه اول n مرتبه و حلقه دوم نیز n مرتبه تکرار می‌شود. 

در آخرین، خط دستور return را داریم که بعد از حلقه اجرا می‌شود و مقدار ثابت 1 را دارد. 

اکنون باید مقادیر به دست آمده را محاسبه کنیم:

n + 1 +n² +1 + n² + 1

2n²n+3

بازهم تنها نماهای مرتبه بالاتر را در نظر بگیرید که 2n² را خواهیم داشت که با صرف نظر از مقدار ثابت به تابع زمانی O(n2) خواهیم رسید.