مقدمه‌ای بر نامپای | سکان آکادمی

همان‌طور که در قسمت معرفی و آماده کردن لوازم اشاره شد، کار کردن با آرایه‌ها نسبت به لیست‌ها سریع‌تر و ساده‌تر است.در برنامه‌نویسی پایتون، لیست‌ها یکی از پرکاربردترین ساختارهای داده محسوب می‌شوند و برای بسیاری از مسائل روزمره پاسخ‌گو هستند. با این حال، زمانی که حجم داده‌ها افزایش پیدا می‌کند یا انجام محاسبات عددی با کارایی بالا مطرح می‌شود، استفاده از لیست‌های معمولی دیگر گزینه‌ی مناسبی نخواهد بود. کتابخانه NumPy به‌عنوان یکی از مهم‌ترین ابزارهای محاسبات عددی در پایتون، با ارائه‌ی ساختاری بهینه برای کار با داده‌ها، این محدودیت را برطرف می‌کند.

در این قسمت از دوره آموزش NumPy، ابتدا آرایه‌های NumPy با لیست‌های پایتون مقایسه می‌شوند، سپس با ساختار کلی این کتابخانه و نحوه‌ی import کردن آن آشنا می‌شوید. در ادامه نیز روش‌های مختلف ایجاد آرایه‌ها (Array) بررسی خواهد شد تا پایه‌ی لازم برای مباحث پیشرفته‌تر فراهم شود.

تفاوت آرایه‌های NumPy با لیست‌های پایتون

همان‌طور که در قسمت قبلی اشاره شد، کار کردن با آرایه‌ها نسبت به لیست‌ها سریع‌تر و ساده‌تر است. به همین دلیل، در محاسبات فنی و سناریوهایی که سرعت پردازش اهمیت بالایی دارد، استفاده از آرایه‌ها گزینه مناسب‌تری محسوب می‌شود. یکی از دلایل اصلی این برتری، تفاوت در نحوه ذخیره‌سازی و بازیابی داده‌ها در حافظه است. آرایه‌های NumPy به شکلی طراحی شده‌اند که استفاده بهینه‌تری از حافظه داشته باشند و همین موضوع باعث افزایش سرعت پردازش آن‌ها می‌شود. علاوه بر این، این ساختارها برای پردازنده‌های مدرن (CPU) های جدید بهینه‌سازی شده‌اند و عملکرد بهتری روی آن‌ها دارند.

یکی دیگر از تفاوت‌های مهم، سینتکس ساده‌تر و خواناتر برای انجام برخی عملیات‌هاست. در لیست‌های پایتون می‌توان انواع مختلفی از داده‌ها را به‌صورت هم‌زمان نگهداری کرد؛ برای مثال:

عدد
مقدار بولی (True / False)
رشته (String)

اما در آرایه‌های NumPy، تمام عناصر باید از یک نوع داده باشند. یعنی یک آرایه یا کاملاً عددی است، یا کاملاً بولی، یا کاملاً رشته‌ای. امکان ترکیب انواع مختلف داده مانند لیست‌ها وجود ندارد. در عوض، آرایه‌های NumPy:

فضای کمتری در حافظه اشغال می‌کنند
ساختار معنادار و مشخصی دارند
می‌توان آن‌ها را بر اساس مفهومشان نام‌گذاری کرد، مانند:
بردار (Vector)
ماتریس (Matrix)
و ساختارهای پیشرفته‌تر

ساختار و ابعاد آرایه‌های NumPy

آرایه‌های NumPy از نظر مفهومی دارای ویژگی‌ای به نام بعد (Dimension) هستند. این مفهوم مشابه مفاهیمی است که در هندسه با آن‌ها آشنا هستیم. برای درک بهتر:

یک نقطه را می‌توان یک شیء صفر بعدی در نظر گرفت
اتصال چند نقطه، یک خط ایجاد می‌کند که یک‌بعدی است
اتصال چند خط، یک صفحه دو‌بعدی می‌سازد
و اتصال چند صفحه، یک فضای سه‌بعدی ایجاد می‌کند

در NumPy نیز دقیقاً همین منطق وجود دارد:

آرایه صفر بعدی → اسکالر (Scaler)
آرایه یک بعدی → بردار (Vector)
آرایه دو بعدی → ماتریس (Matrix)
آرایه‌های با بیش از سه بعد → تانسور (Tensor)

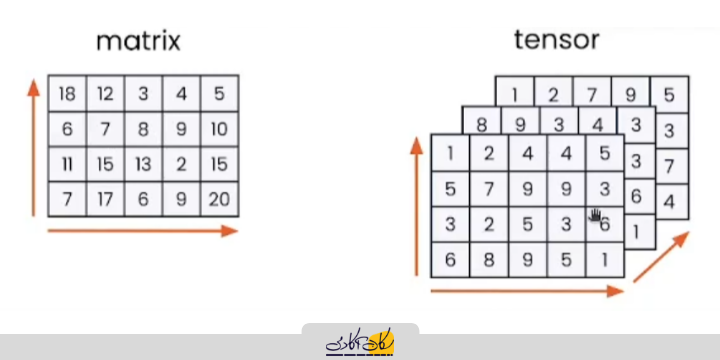
ماتریس یک ساختار دو بعدی است و می‌توان آن را به‌صورت یک صفحه در نظر گرفت. در مقابل، تانسور از قرار گرفتن چندین صفحه (ماتریس) در کنار یکدیگر تشکیل می‌شود و ساختاری با بیش از دو بعد دارد. به بیان ساده:

ماتریس → داده‌های صفحه‌ای (دو بعدی)
تانسور → مجموعه‌ای از چند صفحه که یک ساختار چندبعدی را ایجاد می‌کنند

محور (Axis) در آرایه‌های NumPy

یکی دیگر از مفاهیم مهم در کار با آرایه‌های NumPy ، مفهوم محور (Axis) است. شناخت محور‌ها اهمیت زیادی دارد، زیرا برای دسترسی به عناصر آرایه، آدرس‌دهی و ایندکس گذاری باید بدانیم در امتداد کدام محور حرکت می‌کنیم. در NumPy، شماره‌گذاری محور‌ها از صفر شروع می‌شود و تعداد محور‌ها همیشه یک واحد کمتر از تعداد ابعاد آرایه است. به‌عنوان مثال:

در یک آرایه یک‌بعدی، تنها یک محور وجود دارد که به آن محور صفر (Axis 0) گفته می‌شود.
در یک آرایه دو‌بعدی، دو محور داریم: محور صفر (حرکت در راستای سطرها)محور یک (حرکت در راستای ستون‌ها)

به‌طور کلی، برای حرکت در هر بعد از آرایه، از محور متناظر با آن بعد استفاده می‌کنیم.

نحوه import کردن کتابخانه NumPy

حال به این موضوع می‌رسیم که چگونه از NumPy در پایتون استفاده کنیم. همان‌طور که می‌دانید، برای استفاده از قابلیت‌های پیشرفته در پایتون، لازم است کتابخانه‌های موردنظر را از قبل import کنیم. برای استفاده از NumPy نیز از سینتکس استاندارد زیر استفاده می‌کنیم که در ادامه آن را بررسی خواهیم کرد.

# import numpy here
import numpy as np

به‌طور معمول و طبق یک روال متداول در پروژه‌های پایتونی، کتابخانه NumPy را با نام اختصاری np ایمپورت می‌کنند. این کار باعث می‌شود کدنویسی خواناتر، کوتاه‌تر و استانداردتر باشد و تقریباً در تمام پروژه‌ها و مستندات آموزشی نیز از همین نام‌گذاری استفاده می‌شود. برای افزایش سرعت کار، معمولاً از محیط‌های Notebook استفاده می‌کنیم. در این محیط‌ها، هر دستوری که بنویسیم با فشردن کلید Enter (یا Shift + Enter) اجرا می‌شود. پس از اجرای هر دستور:

یک شماره اجرا (Execution Count) به آن اختصاص داده می‌شود که نشان می‌دهد این دستور چندمین اجرای ما در نوت‌بوک است.
همچنین زمان اجرای سلول ثبت می‌شود و مشخص می‌کند این بخش از کد در چه زمانی اجرا شده است.

این ویژگی‌ها کمک می‌کنند روند اجرای کدها را بهتر دنبال کنیم و ترتیب اجرای دستورات را بدانیم. برای ساخت آرایه در NumPy، روش‌های مختلفی وجود دارد. در این بخش به برخی از این روش‌ها اشاره می‌کنیم و روش‌های تکمیلی را در جلسه بعد بررسی خواهیم کرد.

ساخت آرایه با تبدیل لیست پایتون

اولین و ساده‌ترین روش برای ساخت یک آرایه در NumPy این است که یک لیست پایتونی از قبل داشته باشیم و آن را به آرایه NumPy تبدیل کنیم. در این حالت، ابتدا یک لیست در پایتون تعریف می‌کنیم و سپس با استفاده از توابع NumPy، آن را به یک آرایه (ndarray) تبدیل می‌کنیم. در ادامه، یک لیست پایتونی داریم که عناصر آن همان مقادیری هستند که در اینجا مشاهده می‌کنید.

# a simple list
python_list = [3, 2, 5, 8]

فرض کنید قصد داریم از یک لیست پایتونی، یک آرایه NumPy بسازیم.
برای این کار، ابتدا یک متغیر تعریف می‌کنیم که لیست موردنظر در آن قرار دارد. این مرحله کاملاً طبیعی و مطابق روال معمول پایتون است.

# a simple list
python_list = [3, 2, 5, 8]
my_array = np.array(python_list)

سپس برای ساخت آرایه، از کتابخانه NumPy استفاده می‌کنیم که آن را با نام اختصاری np ایمپورت کرده‌ایم. در NumPy متدی به نام array وجود دارد که برای ساخت آرایه استفاده می‌شود. این متد می‌تواند آرگومان‌های مختلفی دریافت کند، اما در ساده‌ترین حالت، برای تبدیل یک لیست به آرایه، کافی است خود لیست پایتون را به آن پاس بدهیم. پس کاری که انجام می‌دهیم این است که:

نام لیست پایتونی را به متد array می‌دهیم
خروجی این متد، یک آرایه NumPy خواهد بود

# a simple list
python_list = [3, 2, 5, 8]
my_array = np.array(python_list)
my_array

# خروجی: array([3, 2, 5, 8])

اگر این آرایه را نمایش دهیم، مشاهده می‌کنیم که:

عناصر آن دقیقاً همان عناصر لیست پایتونی هستند
با این تفاوت که حالا این داده‌ها به یک آرایه NumPy تبدیل شده‌اند

اگر از این آرایه type بگیریم و آن را اجرا کنیم، می‌بینیم که:

یک آبجکت از نوع numpy.ndarray ساخته شده است
این نوع داده با لیست پایتون تفاوت دارد

# a simple list
python_list = [3, 2, 5, 8]
my_array = np.array(python_list)
type(my_array)

# خروجی: numpy.ndarray

در حالی که:

اگر از یک لیست پایتونی type بگیریم، خروجی list خواهد بود
اما آرایه NumPy از نوع ndarray است و رفتار و قابلیت‌های متفاوتی دارد

# a simple list
python_list = [3, 2, 5, 8]
my_array = np.array(python_list)
type(python_list)

# خروجی: list

بررسی بُعد (Dimension) آرایه

قبلاً درباره مفهوم بعد (Dimension) صحبت کردیم و گفتیم که هر آرایه می‌تواند صفر بعدی، یک‌بعدی، دو‌بعدی و یا بیشتر باشد. در این مثال، چون آرایه از یک لیست ساده ساخته شده است، می‌دانیم که:

این آرایه یک‌بعدی است
و در واقع با یک بردار (Vector) سروکار داریم

اما اگر آرایه‌ای داشته باشیم و ندانیم چند بعد دارد، NumPy یک ویژگی (Property) در اختیار ما قرار می‌دهد. برای تشخیص تعداد ابعاد یک آرایه NumPy، می‌توانیم از ویژگی ndim استفاده کنیم. این ویژگی روی آبجکت ndarray قرار دارد و تعداد ابعاد آرایه را به ما برمی‌گرداند. به این شکل می‌توان بررسی کرد که یک آرایه چندبعدی است و ساختار آن چگونه تعریف شده است. اگر ویژگی ndim را اجرا کنیم، خروجی عدد ۱ خواهد بود. این عدد نشان می‌دهد که آرایه‌ای که ساخته‌ایم یک‌بعدی است.

# a simple list
python_list = [3, 2, 5, 8]
my_array = np.array(python_list)
my_array.ndim

# 1

تعیین بعد هنگام ساخت آرایه

در NumPy این امکان وجود دارد که هنگام ساخت آرایه، تعداد ابعاد (Dimension) را به‌صورت مستقیم مشخص کنیم. برای مثال، می‌توانیم به NumPy اعلام کنیم که آرایه‌ای با ۳ بعد برای ما ایجاد کند. در این حالت، اگر مقدار ndim را بررسی کنیم، نتیجه ۳ خواهد بود.

# a simple list
python_list = [3, 2, 5, 8]
my_array = np.array(python_list, ndmin=3)
my_array.ndim

# 3

اما سؤال مهم اینجاست که NumPy این ساختار را چگونه ایجاد می‌کند؟
زمانی که تعداد ابعاد بیشتری نسبت به داده اولیه مشخص می‌کنیم، NumPy در واقع برای ما فضاهای خالی مفهومی ایجاد می‌کند.

# a simple list
python_list = [3, 2, 5, 8]
my_array = np.array(python_list, ndmin=3)
my_array

# خروجی: array([[[3, 2, 5, 8]]])

اگر خروجی آرایه را با حالت قبلی مقایسه کنیم، مشاهده می‌کنیم که تعدادی کروشه (Bracket) به ساختار آرایه اضافه شده است برای اینکه این موضوع بهتر در ذهن بماند، یک قانون ساده را در نظر بگیرید، هر جفت کروشه باز و بسته ([]) نشان‌دهنده یک بعد از آرایه است.

در واقع NumPy، ابعادی را که به‌صورت طبیعی در لیست پایتون وجود ندارند، با استفاده از این کروشه‌ها نمایش می‌دهد و ساختار چندبعدی را برای ما شبیه‌سازی می‌کند.

ساخت آرایه از لیست‌های تو در تو (Nested List)

حال این سؤال مطرح می‌شود که اگر یک لیست تو در تو داشته باشیم، یعنی داخل عناصر یک لیست، لیست‌های دیگری هم وجود داشته باشد، آیا می‌توان از آن آرایه NumPy ساخت؟

برای پاسخ به این سؤال، بیایید آن را بررسی کنیم. در محیط Notebook می‌توانیم با استفاده از کلیدهای میانبر:

کلید B برای ایجاد سلول جدید در پایین
کلید A برای ایجاد سلول جدید در بالا

یک لیست تو در تو تعریف کنیم. سپس، دقیقاً با همان دستوری که قبلاً استفاده کردیم، می‌توانیم این لیست را به یک آرایه NumPy تبدیل کنیم. نتیجه‌ای که دریافت می‌کنیم یک آرایه دو بعدی خواهد بود

# a nested list
my_list = [[3,2,5],
           [9,7,1],
           [4,3,6]]
print("my list: " ,my_list)

my_ndarray = np.array(my_list)
print("my array: \n", my_ndarray)

# خروجی: my list: [[3, 2, 5], [9, 7, 1], [4, 3, 6]]
# my array: 
# [[3 2 5]
# [9 7 1]
# [4 3 6]]

در یک آرایه دو بعدی:

ابتدا سطرها را در نظر می‌گیریم
سپس ستون‌ها را می‌شماریم

آرایه‌ای که برای ما ساخته می‌شود، دقیقاً بر اساس همین منطق سطر و ستون سازمان‌دهی شده است و می‌توان آن را به‌صورت یک ماتریس در نظر گرفت.

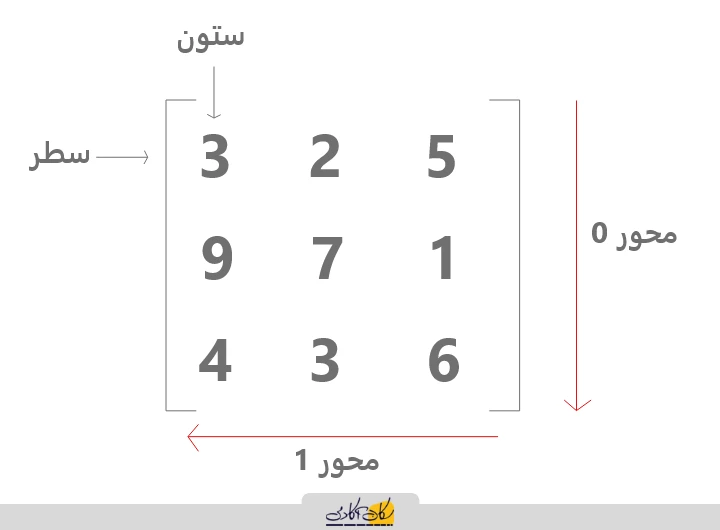
اگر مثلا ما بخواهیم شماره 7 را پیدا کنیم ایندکس آن میشود 1،1 فراموش نشود که ایندکس گذاری از 0 شروع میشود.

برای دیدن ادامه این جلسه در قسمت بعد با ما همراه باشید.